Лекция 4. Предобработка данных

Необходимые этапы нейросетевого анализа

Теперь, после знакомства с базовыми принципами нейросетевой обработки, можно приступать к практическим применениям полученных знаний для решения конкретных задач. Первое, с чем сталкивается пользователь любого нейропакета - это необходимость подготовки данных для нейросети. До сих пор мы не касались этого, вообще говоря, непростого вопроса, молчаливо предполагая, что данные для обучения уже имеются и представлены в виде, доступном для нейросети. На практике же именно предобработка данных может стать наиболее трудоемким элементом нейросетевого анализа. Причем, знание основных принципов и приемов предобработки данных не менее, а может быть даже более важно, чем знание собственно нейросетевых алгоритмов. Последние как правило, уже "зашиты" в различных нейроэмуляторах, доступных на рынке. Сам же процесс решения прикладных задач, в том числе и подготовка данных, целиком ложится на плечи пользователя. Данная глава призвана заполнить этот пробел в описании технологии нейросетевого анализа.

Для начала выпишем с небольшими комментариями всю технологическую цепочку, т.е. необходимые этапы нейросетевого анализа:

  Кодирование входов-выходов: нейросети могут работать только с числами.

  Нормировка данных: результаты нейроанализа не должны зависеть от выбора единиц измерения.

  Предобработка данных: удаление очевидных регулярностей из данных облегчает нейросети выявление нетривиальных закономерностей.

  Обучение нескольких нейросетей с различной архитектурой: результат обучения зависит как от размеров сети, так и от ее начальной конфигурации.

  Отбор оптимальных сетей: тех, которые дадут наименьшую ошибку предсказания на неизвестных пока данных.

  Оценка значимости предсказаний: оценка ошибки предсказаний не менее важна, чем само предсказанное значение.

Если до сих пор мы ограничивали наше рассмотрение, в основном, последними этапами, связанными с обучением собственно нейросетей, то в этой главе мы сосредоточимся на первых этапах нейросетевого анализа - предобработке данных. Хотя перобработка не связана непосредственно с нейросетями, она является одним из ключевых элементов этой информационной технологии. Успех обучения нейросети может решающим образом зависеть от того, в каком виде представлена информация для ее обучения.

В этой главе мы рассмотрим предобработку данных для обучения с учителем и постараемся, главным образом, выделить и проиллюстрировать на конкретных примерах основной принцип такой предобработки: увеличение информативности примеров для повышения эффективности обучения.

Кодирование входов-выходов

В отличие от обычных компьютеров, способных обрабатывать любую символьную информацию, нейросетевые алгоритмы работают только с числами, ибо их работа базируется на арифметических операциях умножения и сложения. Именно таким образом набор синаптических весов определяет ход обработки данных.

Между тем, не всякая входная или выходная переменная в исходном виде может иметь численное выражение. Соответственно, все такие переменные следует закодировать - перевести в численную форму, прежде чем начать собственно нейросетевую обработку. Рассмотрим, прежде всего основной руководящий принцип, общий для всех этапов предобработки данных.

 

Максимизация энтропии как цель предобработки

Допустим, что в результате перевода всех данных в числовую форму и последующей нормировки все входные и выходные переменные отображаются в единичном кубе. Задача нейросетевого моделирования - найти статистически достоверные зависимости между входными и выходными переменными. Единственным источником информации для статистического моделирования являются примеры из обучающей выборки. Чем больше бит информации принесет каждый пример - тем лучше используются имеющиеся в нашем распоряжения даные.

Рассмотрим произвольную компоненту нормированных (предобработанных) данных: . Среднее количество информации, приносимой каждым примером , равно энтропии распределения значений этой компоненты . Если эти значения сосредоточены в относительно небольшой области единичного интервала, информационное содержание такой компоненты мало. В пределе нулевой энтропии, когда все значения переменной совпадают, эта переменная не несет никакой информации. Напротив, если значения переменной равномерно распределены в единичном интервале, информация такой переменной максимальна.

Общий принцип предобработки данных для обучения, таким образом, состоит в максимизации энтропии входов и выходов. Этим принципом следует руководствоваться и на этапе кодирования нечисловых переменных.

 

Типы нечисловых переменных

Можно выделить два основных типа нечисловых переменных: упорядоченные (называемые также ординальными - от англ. order - порядок) и категориальные. В обоих случаях переменная относится к одному из дискретного набора классов . Но в первом случае эти классы упорядочены - их можно ранжировать: , тогда как во втором такая упорядоченность отсутствует. В качестве примера упорядоченных переменных можно привести сравнительные категории: плохо - хорошо - отлично, или медленно - быстро. Категориальные переменные просто обозначают один из классов, являются именами категорий. Например, это могут быть имена людей или названия цветов: белый, синий, красный.

 

Кодирование ординальных переменных

Ординальные переменные более близки к числовой форме, т.к. числовой ряд также упорядочен. Соответственно, для кодирования таких переменных остается лишь поставить в соответствие номерам категорий такие числовые значения, которые сохраняли бы существующую упорядоченность. Естественно, при этом имеется большая свобода выбора - любая монотонная функция от номера класса порождает свой способ кодирования. Какая же из бесконечного многообразия монотонных функций - наилучшая?

В соответствии с изложенным выше общим принципом, мы должны стремиться к тому, чтобы максимизировать энтропию закодированных данных. При использовании сигмоидных функций активации все выходные значения лежат в конечном интервале - обычно или . Из всех статистических функций распределения, определенных на конечном интервале, максимальной энтропией обладает равномерное распределение.

Применительно к данному случаю это подразумевает, что кодирование переменных числовыми значениями должно приводить, по возможности, к равномерному заполнению единичного интервала закодированными примерами. (Захватывая заодно и этап нормировки.) При таком способе "оцифровки" все примеры будут нести примерно одинаковую информационную нагрузку.

Исходя из этих соображений, можно предложить следующий практический рецепт кодирования ординальных переменных. Единичный отрезок разбивается на отрезков - по числу классов - с длинами пропорциональными числу примеров каждого класса в обучающей выборке:

, где - число примеров класса , а , как обычно, общее число примеров. Центр каждого такого отрезка будет являться численным значением для соответствующего ординального класса (см. Рисунок 24).

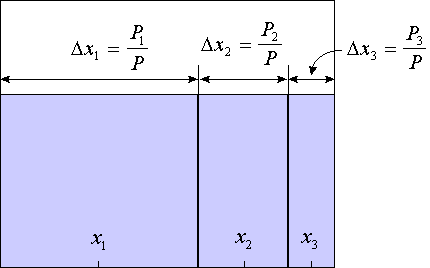
Рисунок 24. Илюстрация способа кодирования кардинальных переменных с учетом количества примеров каждой категории.

Кодирование категориальных переменных

В принципе, категориальные переменные также можно закодировать описанным выше способом, пронумеровав их произвольным образом. Однако, такое навязывание несуществующей упорядоченности только затруднит решение задачи. Оптимальное кодирование не должно искажать структуры соотношений между классами. Если классы не упорядоченны, такова же должна быть и схема кодирования.

Наиболее естественной выглядит и чаще всего используется на практике двоичное кодирование типа "", когда имена категорий кодируются значениями бинарных нейронов, причем первая категория кодируется как , вторая, соответственно - и т.д. вплоть до -ной: . (Можно использовать биполярную кодировку, в которой нули заменяются на "".) Легко убедиться, что в такой симметричной кодировке расстояния между всеми векторами-категориями равны.

Такое кодирование, однако, неоптимально в случае, когда классы представлены существенно различающимся числом примеров. В этом случае, функция распределения значений переменной крайне неоднородна, что существенно снижает информативность этой переменной. Тогда имеет смысл использовать более компактный, но симметричный код , когда имена классов кодируются -битным двоичным кодом. Причем, в новой кодировке активность кодирующих нейронов должна быть равномерна: иметь приблизительно одинаковое среднее по примерам значение активации. Это гарантирует одинаковую значимость весов, соответствующих различным нейронам.

В качестве примера рассмотрим ситуацию, когда один из четырех классов (например, класс ) некой категориальной переменной представлен гораздо большим числом примеров, чем остальные: . Простое кодирование привело бы к тому, что первый нейрон активировался бы гораздо чаще остальных. Соответственно, веса оставшихся нейронов имели бы меньше возможностей для обучения. Этой ситуации можно избежать, закодировав четыре класса двумя бинарными нейронами следующим образом: , обеспечивающим равномерную "загрузку" кодирующих нейронов.

 

Отличие между входными и выходными переменными

В заключении данного раздела отметим одно существенное отличие способов кодирования входных и выходных переменных, вытекающее из определения градиента ошибки: . А именно, входы участвуют в обучении непосредственно, тогда как выходы - лишь опосредованно - через ошибку верхнего слоя. Поэтому при кодировании категорий в качестве выходных нейронов можно использовать как логистическую функцию активации , определенную на отрезке , так и ее антисимметричный аналог для отрезка , например: . При этом кодировка выходных переменных из обучающей выборки будет либо , либо . Выбор того или иного варианта никак не скажется на обучении.

В случае со входными переменными дело обстоит по-другому: обучение весов нижнего слоя сети определяется непосредственно значениями входов: на них умножаются невязки, зависящие от выходов. Между тем, если с точки зрения операции умножения значения равноправны, между 0 и 1 имеется существенная асимметрия: нулевые значения не дают никакого вклада в градиент ошибки. Таким образом, выбор схемы кодирования входов влияет на процесс обучения. В силу логической равноправности обоих значений входов, более предпочтительной выглядит симметричная кодировка: , сохраняющая это равноправие в процессе обучения.

Нормировка и предобработка данных

Как входами, так и выходами нейросети могут быть совершенно разнородные величины. Очевидно, что результаты нейросетевого моделирования не должны зависеть от единиц измерения этих величин. А именно, чтобы сеть трактовала их значения единообразно, все входные и выходные величины должны быть приведены к единому - единичному - масштабу. Кроме того, для повышения скорости и качества обучения полезно провести дополнительную предобработку данных, выравнивающую распределение значений еще до этапа обучения.

 

Индивидуальная нормировка данных

Приведение данных к единичному масштабу обеспечивается нормировкой каждой переменной на диапазон разброса ее значений. В простейшем варианте это - линейное преобразование:

в единичный отрезок: . Обобщение для отображения данных в интервал , рекомендуемого для входных данных тривиально.

Линейная нормировка оптимальна, когда значения переменной плотно заполняют определенный интервал. Но подобный "прямолинейный" подход применим далеко не всегда. Так, если в данных имеются относительно редкие выбросы, намного превышающие типичный разброс, именно эти выбросы определят согласно предыдущей формуле масштаб нормировки. Это приведет к тому, что основная масса значений нормированной переменной сосредоточится вблизи нуля: .

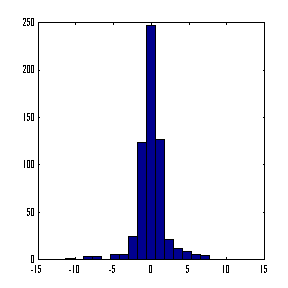
Рисунок 25. Гистограмма значений переменной при наличии редких, но больших по амплитуде отклонений от среднего

Гораздо надежнее, поэтому, ориентироваться при нормировке не на экстремальные значения, а на типичные, т.е. статистические характеристики данных, такие как среднее и дисперсия:

.

В этом случае основная масса данных будет иметь единичный масштаб, т.е. типичные значения всех переменных будут сравнимы (см. Рисунок 25).

Однако, теперь нормированные величины не принадлежат гарантированно единичному интервалу, более того, максимальный разброс значений заранее не известен. Для входных данных это может быть и не важно, но выходные переменные будут использоваться в качестве эталонов для выходных нейронов. В случае, если выходные нейроны - сигмоидные, они могут принимать значения лишь в единичном диапазоне. Чтобы установить соответствие между обучающей выборкой и нейросетью в этом случае необходимо ограничить диапазон изменения переменных.

Линейное преобразование, как мы убедились, неспособно отнормировать основную массу данных и одновременно ограничить диапазон возможных значений этих данных. Естественный выход из этой ситуации - использовать для предобработки данных функцию активации тех же нейронов. Например, нелинейное преобразование

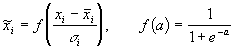
нормирует основную массу данных одновременно гарантируя, что (см. Рисунок 26).

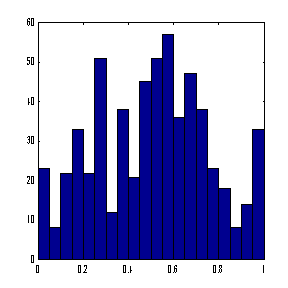
Рисунок 26. Нелинейная нормировка, использующая логистическую функцию активации

Как видно из приведенного выше рисунка, распределение значений после такого нелинейного преобразования гораздо ближе к равномерному.

До сих пор мы старались максимизировать энтропию каждого входа (выхода) по отдельности. Но, вообще говоря, можно добиться гораздо большего максимизируя их совместную энтропию. Рассмотрим эту технику на примере совместной нормировки входов, подразумевая, что с таким же успехом ее можно применять и для выходов а также для всей совокупности входов-выходов.

 

Совместная нормировка: выбеливание входов

Если два входа статистически не независимы, то их совместная энтропия меньше суммы индивидуальных энтропий: . Поэтому добившись статистической независимости входов мы, тем самым, повысим информационную насыщенность входной информации. Это, однако, потребует более сложной процедуры совместной нормировки входов.

Вместо того, чтобы использовать для нормировки индивидуальные дисперсии, будем рассматривать входные данные в совокупности. Мы хотим найти такое линейное преобразование, которое максимизировало бы их совместную энтропию. Для упрощения задачи вместо более сложного условия статистической независимости потребуем, чтобы новые входы после такого преобразования были декоррелированы. Для этого рассчитаем средний вектор и ковариационную матрицу данных по формулам:

Затем найдем линейное преобразование, диагонализующее ковариационную матрицу. Соответствующая матрица составлена из столбцов - собственных векторов ковариационной матрицы:

Легко убедиться, что линейное преобразование, называемое выбеливанием (whitening)

превратит все входы в некоррелированные величины с нулевым средним и единичной дисперсией.

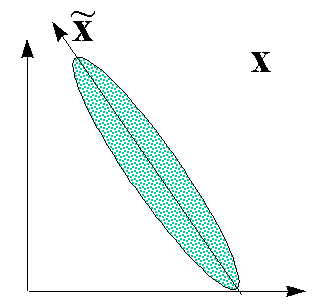
Если входные данные представляют собой многомерный эллипсоид, то графически выбеливание выглядит как растяжение этого эллипсоида по его главным осям (Рисунок 27).

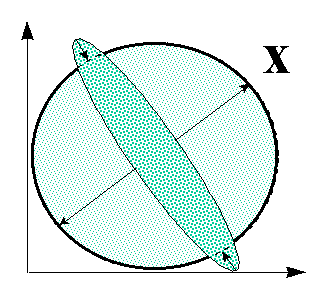
Рисунок 27. Выбеливание входной информации: повышение информативности входов за счет выравнивания функции распределения

Очевидно, такое преобразование увеличивает совместную энтропию входов, т.к. оно выравнивает распределение данных в обучающей выборке.

Понижение размерности входов

Сильной стороной нейроанализа является возможность получения предсказаний при минимуме априорных знаний. Поскольку заранее обычно неизвестно насколько полезны те или иные входные переменные для предсказания значений выходов, возникает соблазн увеличивать число входных параметров, в надежде на то, что сеть сама определит какие из них наиболее значимы. Однако, как это уже обсуждалось в Главе 3, сложность обучения персептронов быстро возрастает с ростом числа входов (а именно - как куб размерности входных данных ). Еще важнее, что с увеличением числа входов страдает и точность предсказаний, т.к. увеличение числа весов в сети снижает предсказательную способность последней (согласно предыдущим оценкам:).

Таким образом, количество входов приходится довольно жестко лимитировать, и выбор наиболее информативных входных переменных представляет важный этап подготовки данных для обучения нейросетей. Глава 4 специально посвящена использованию для этой цели самих нейросетей, обучаемых без учителя. Не стоит, однако, пренебрегать и традиционными, более простыми и зачастую весьма эффективными методами линейной алгебры.

Один из наиболее простых и распространенных методов понижения размерности - использование главных компонент входных векторов. Этот метод позволяет не отбрасывая конкретные входы учитывать лишь наиболее значимые комбинации их значений.

 

Понижение размерности входов методом главных компонент

Собственные числа матрицы ковариаций, фигурировавшие в предыдущем разделе, являются квадратами дисперсий вдоль ее главных осей. Если между входами существует линейная зависимость, некоторые из этих собственных чисел стремятся к нулю. Таким образом, наличие малых свидетельствует о том, что реальная размерность входных данных объективно ниже, чем число входов. Можно задаться некоторым пороговым значением и ограничиться лишь теми главными компонентами, которые имеют . Тем самым, достигается понижение размерности входов, при минимальных потерях точности представления входной информации.

Рисунок 28. Понижение размерности входов методом главных компонент.

 

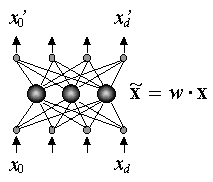
Восстановление пропущенных компонент данных

Главные компоненты оказываются удобным инструментом и для восстановления пропусков во входных данных. Действительно, метод главных компонент дает наилучшее линейное приближение входных данных меньшим числом компонент: (Здесь мы, как и прежде, для учета постоянного члена включаем фиктивную нулевую компоненту входов, всегда равную единице - см. Рисунок 28, где справа показана нейросетевая интерпретация метода главных компонент. Таким образом, - это матрица размерности ). Восстановленные по главным компонентам данные из обучающей выборки имеют наименьшее среднеквадратичное отклонение от своих прототипов . Иными словами, при отсутствии у входного вектора компонент, наиболее вероятное положение этого вектора - на гиперплоскости первых главных компонент. Таким образом, для восстановленного вектора имеем: , причем для известных компонент .

Пусть, например, у вектора неизвестна всего одна, -я координата. Ее значение находится из оставшихся по формуле:

,

где в числителе учитываются лишь известные компоненты входного вектора .

В общем случае восстановить неизвестные компоненты (с индексами из множества ) можно с помощью следующей итеративной процедуры (см. Рисунок 29):

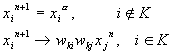
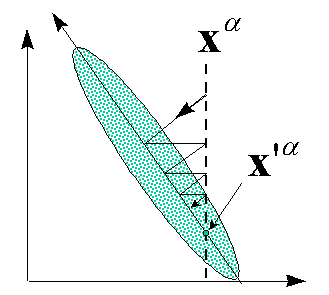
Рисунок 29. Восстановление пропущенных значения с помощью главных компонент. Пунктир - возможные значения исходного вектора с неизвестными координатами. Наиболее вероятное его значение - на пересечении с первыми главными компонентами

Понижение размерности входов с помощью нейросетей

Для более глубокой предобработки входов можно использовать все богатство алгоритмов самообучающихся нейросетей, о которых шла речь ранее. В частности, для оптимального понижения размерности входов можно воспользоваться методом нелинейных главных компонент (см. Рисунок 30).

Рисунок 30. Понижение размерности входов методом нелинейных главных компонент

 

Такие сети с узким горлом также можно использовать для восстановления пропущенных значений - с помощью итерационной процедуры, обобщающей линейный вариант метода главных компонент (см. Рисунок 31).

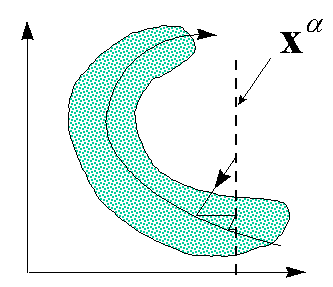
Рисунок 31. Восстановление пропущенных компонент данных с помощью нелинейных главных компонент

Однако, такую глубокую "предобработку" уже можно считать самостоятельной нейросетевой задачей. И мы не будем дале углубляться в этот вопрос.

 

Квантование входов

Более распространенный вид нейросетевой предобработки данных - квантование входов, использующее слой соревновательных нейронов (см. Рисунок 32).

Рисунок 32. Понижение разнообразия входов методом квантования (кластеризации)

 

Нейрон-победитель является прототипом ближайших к нему входных векторов. Квантование входов обычно не сокращает, а наоборот, существенно увеличивает число входных переменных. Поэтому его используют в сочетании с простейшим линейным дискриминатором - однослойным персептороном. Получающаяся в итоге гибридная нейросеть, предложенная Нехт-Нильсеном в 1987 году, обучается послойно: сначала соревновательный слой кластеризует входы, затем выходным весам присваиваются значения выходной функции, соответствующие данному кластеру. Такие сети позволяют относительно быстро получать грубое - кусочно-постоянное - приближение аппроксимируемой функции (см. Рисунок 33).

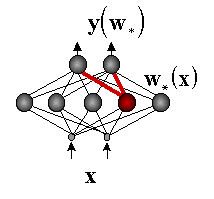
Рисунок 33. Гибридная сеть с соревновательным слоем, дающая кусочно-постоянное приближение функций

Особенно полезны кластеризующие сети для восстановления пропусков в массиве обучающих данных. Поскольку работа соревновательного слоя основана на сравнении расстояний между данными и прототипами, осутствие у входного вектора некоторых компонент не препятствует нахождению прототипа-победителя: сравнение ведется по оставшимся компонентам :

.

При этом все прототипы находятся в одинаковом положении. Рисунок 34 иллюстрирует эту ситуацию.

  

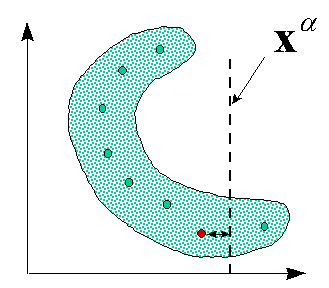
Рисунок 34. Наличие пропущенных компонент не препятствует нахождению ближайшего прототипа по оставшимся компонентам входного вектора

 

Таким образом, слой квантующих входные данные нейронов нечувствителен к пропущенным компонентам, и может служить "защитным экраном" для минимизации последствий от наличия пропусков в обучающей базе данных.

Отбор наиболее значимых входов

До сих пор мы старались лишь представить имеющуюся входную информацию наилучшим - наиболее информативным - образом. Однако, рассмотренные выше методы предобработки входов никак не учитывали зависимость выходов от этих входов. Между тем, наша задача как раз и состоит в выборе входных переменных, наиболее значимых для предсказаний. Для такого более содержательного отбора входов нам потребуются методы, позволяющие оценивать значимость входов.

 

Линейная значимость входов

Легче всего оценить значимость входов в линейной модели, предполагающей линейную зависимость выходов от входов:

Матрицу весов можно получить, например, обучением простейшего - однослойного персептрона с линейной функцией активации. Допустим теперь, что при определении выходов мы опускаем одну, для определенности - -ю компоненту входов, заменяя ее средним значением этой переменной. Это приведет к огрублению модели, т.е. возрастании ошибки на величину:

.

(Полагая, что данные нормированны на их дисперсию.) Таким образом, значимость -го входа определяется суммой квадратов соответствующих ему весов.

Особенно просто определить значимость выбеленных входов. Для достаточно просто вычислить взаимную корреляцию входов и выходов:

.

Действительно, при линейной зависимости между входами и выходами имеем: .

Таким образом, в общем случае для получения матрицы весов требуется решить систему линейных уравнений. Но для предварительно выбеленных входов имеем: , так что в этом случае матрица кросс-корреляций просто совпадает с матрицей весов обученного линейного персептрона: .

Резюмируя, значимость входов в предположении о приблизительно линейной зависимости между входными и выходными переменными для выбеленных входов пропорциональна норме столбцов матрицы кросс-корреляций: .

Не следует, однако, обольщаться существованием столь простого рецепта определения значимости входов. Линейная модель может быть легко построена и без привлечения нейросетей. Реальная сила нейроанализа как раз и состоит в возможности находить более сложные нелинейные зависимости. Более того, для облегчения собственно нелинейного анализа рекомендуется заранее освободиться от тривиальных линейных зависимостей - т.е. в качестве выходов при обучении подавать разность между выходными значениями и их линейным приближением. Это увеличит "разрешающую способность" нейросетевого моделирования (см. Рисунок 35).

Рисунок 35. Выявление нелинейной составляющей функции после вычитания линейной зависимости . (Здесь - гауссовый случайный шум)

 

Для определения "нелинейной" значимости входов - после вычитания линейной составляющей, изложенный выше подход неприменим. Здесь надо привлекать более изощренные методики. К описанию одной из них, алгоритмам box-counting, мы и переходим.

 

Нелинейная значимость входов. Box-counting алгоритмы

Алгортимы box-counting, как следует из самого их названия, основаны на подсчете чисел заполнения примерами ячеек (boxes), на которые специально для этого разбивается пространство переменных . Эти числа заполнения используются для оценки плотности вероятности распределения примеров по ячейкам. Набор вероятностей дает возможность рассчитать любую статистическую характеристику набора данных обучающей выборки.

Для определения значимости входов нам потребуется оценить предсказуемость выходов, обеспечиваемую данным набором входных переменных. Чем выше эта предсказуемость - тем лучше соответствующий набор входов. Таким образом, метод box-counting предоставляет в наше распоряжение технологию отбора наиболее значимых признаков для нейросетевого моделирования, технологию оптимизации входного пространства признаков.

Согласно общим положениям теории информации, мерой предсказуемости случайной величины является ее энтропия, , определяемая как среднее значение ее логарифма. В методике box-counting энтропия приближенно оценивается по набору чисел заполнения ячеек, на которые разбивается интервал ее возможных значений: . Качественно, энтропия есть логарифм эффективного числа заполненных ячеек (см. Рисунок 36). Чем больше энтропия переменной, тем менее предсказуемо ее значение. Когда все значения примеров сосредоточены в одной ячейке - их энтропия равна нулю, т.к. положение данных определено (с данной степенью точности). Равномерному заполнению ячеек соответствует максимальная энтропия - наибольший разброс возможных значений переменной.

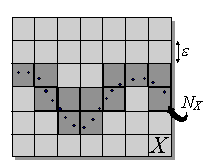
Рисунок 36. Смысл энтропии - эффективное число заполненных данными ячеек

Предсказуемость случайного вектора, обеспечиваемое знанием другой случайной величины , дается кросс-энтропией:

Качественно, кросс-энтропия равна логарифму отношения типичного разброса значений переменной к типичному разбросу этой переменной, но при известном значении переменной (см. Рисунок 37):

.

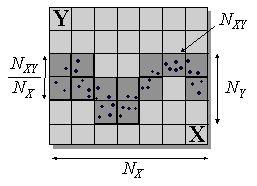
Рисунок 37. Иллюстрация к понятию кросс-энтропии: - полное число ячеек в объединенном пространстве , - число проекций ячеек на пространство , - характерный разброс по оси при фиксированном , - характерный разброс всех данных по оси .

 

Чем больше кросс-энтропия, тем больше определенности вносит знание значения в предсказание значения переменной .

Описанный выше энтропийный анализ не использует никаких предположений о характере зависимости между входными и выходными переменными. Таким образом, данная методика дает наиболее общий рецепт определения значимости входов, позволяя также оценивать степень предсказуемости выходов.

В принципе, качество предсказаний и, соответственно, значимость входной информации определяется, в конечном итоге, в результате обучения нейросети, которая, к тому же, дает решение в явном виде. Однако, как мы знаем, обучение нейросети - довольно сложная вычислительная задача (требующая операций). Между тем, существуют эффективные алгоритмы быстрого подсчета кросс-энтропии (с вычислительной сложностью ), намного более экономные, чем обучение нейросетей. Значение методики box-counting состоит в том, что не находя самого решения, она позволяет быстро предсказать качество этого прогноза. Поэтому эта методика может быть положена в основу предварительного отбора входной информации на этапе предобработки данных.

 

Формирование оптимального пространства признаков

В типичной ситуации набор выходных, прогнозируемых, переменных фиксирован, и требуется подобрать наилучшую комбинацию ограниченного числа входных величин. Оценка значимости входов позволяет построить процедуру систематического предварительного подбора входных переменных - до этапа обучения нейросети. Для иллюстрации опишем две возможные стратеги автоматического формирования признакого пространства.

Последовательное добавление наиболее значимых входов

Один из наиболее очевидных способов формирования пространства признаков с учетом реальной значимости входов - постепенный подбор наиболее значимых входов в качестве очередных признаков. В качестве первого признака выбирается вход с наибольшей индивидуальной значимостью:

. .

Вторым признаком становится вход, обеспечивающий наибольшую предсказуемость в паре с уже выбранным:

,

и так далее. На каждом следующем этапе добавляется вход, наиболее значимый в компании с выбранными ранее входами:

.

Такая процедура не гарантирует нахождения наилучшей комбинации входов, т.е. дает субоптимальный набор признаков, т.к. реально рассматривается лишь очень малая доля от полного числа комбинаций входов, и значимость каждого нового признака зависит от сделанного прежде выбора. Полный перебор, однако, практически неосуществим: выбор оптимальной комбинации входов при полном их числе требует перебора 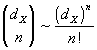комбинаций.

Другим недостатком описанного выше подхода является необходимость подсчета кросс-энтропии в пространстве все более высокой размерности по мере увеличения числа отобранных признаков. Ниже описана процедура, свободная от этого недостатка, основанная на применении методики box-counting лишь в низкоразмерных пространствах (а именно - с размерностью ).

Формирование признакого пространства методом ортогонализации

Следующая систематическая процедура способна итеративно выделять наиболее значимые признаки, являющиеся линейными комбинациями входных переменных: (подмножество входов является частным случаем линейной комбинации, т.е. формально можно найти лучшее решение, чем то, что доступно путем отбора наиболее значимых комбинаций входов).

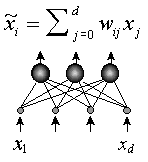
Рисунок 38. Выбор наиболее значимых линейных комбинаций входных переменных.

Для определения значимости каждой входной компоненты будем использовать каждый раз индивидуальную значимость этого входа:.

Подсчитав индивидуальную значимость входов, находим направление в исходном входном пространстве, отвечающее наибольшей (нелинейной) чувствительности выходов к изменению входов. Это градиентное направление определит первый вектор весов, дающий первую компоненту пространства признаков:

.

Следующую компоненту будем искать аналогично первой, но уже в пространстве перпендикулярном выбранному направлению, для чего спроектируем все входные вектора в это пространство:

.

В этом пространстве можно опять подсчитать "градиент" предсказуемости, определив индивидуальную значимость спроектированных входов, и так далее. На каждом следующем этапе подсчитывается индивидуальная значимость для проекции входов

,

что не требует повышения размерности box-counting анализа. Таким образом, описанная выше процедура позволяет формировать пространство признаков произвольной размерности - без потери точности.

Заключение

Конечно, описанными выше методиками не исчерпывается все разнообразие подходов к ключевой для нейро-анализа проблеме формирования пространства признаков. Мы не упомянули, в частности, генетические алгоритмы, которые в совокупностью с методикой box-counting являются весьма перспективным инструментом. Ничего не было сказано также о методике разделения независимых компонент (blind signal separation), расширяющей анализ главных компонент. Необъятного не объять. Главное, чтобы за деталями не затерялся основополагающий принцип предобработки данных: снижение существующей избыточности всеми возможными способами. Это повышает информативность примеров и, тем самым, качество нейропредсказаний.