Лекция 3. Обучение без учителя: Сжатие информации

Обобщение данных. Прототипы задач

В этой главе рассматривается новый тип обучения нейросетей - обучение без учителя (или для краткости - самообучение), когда сеть самостоятельно формирует свои выходы, адаптируясь к поступающим на ее входы сигналам. Как и прежде, такое обучение предполагает минимизацию некоторого целевого функционала. Задание такого функционала формирует цель, в соответствии с которой сеть осуществляет преобразование входной информации.

В отсутствие внешней цели, "учителем" сети могут служить лишь сами данные, т.е. имеющаяся в них информация, закономерности, отличающие входные данные от случайного шума. Лишь такая избыточность позволяет находить более компактное описание данных, что, согласно общему принципу, изложенному в предыдущей главе, и является обобщением эмпирических данных. Сжатие данных, уменьшение степени их избыточности, использующее существующие в них закономерности, может существенно облегчить последующую работу с данными, выделяя действительно независимые признаки. Поэтому самообучающиеся сети чаще всего используются именно для предобработки "сырых" данных. Практически, адаптивные сети кодируют входную информацию наиболее компактным при заданных ограничениях кодом.

Длина описания данных пропорциональна, во-первых, разрядности данных (т.е. числу бит), определяющей возможное разнообразие принимаемых ими значений, и, во-вторых, размерности даных , т.е. числу компонент входных векторов . Соответственно, можно различить два предельных типа кодирования, использующих противоположные способы сжатия информации:

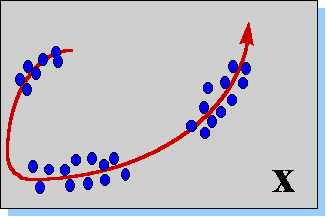
  Понижение размерности данных с минимальной потерей информации. (Сети, например, способны осуществлять анализ главных компонент данных, выделять наборы независимых признаков.)

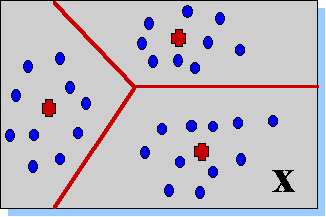
  Уменьшение разнообразия данных за счет выделения конечного набора прототипов, и отнесения данных к одному из таких типов. (Кластеризация данных, квантование непрерывной входной информации.)

a

b

Рисунок 12. Два типа сжатия информации. Понижение размерности (a) позволяет описывать данные меньшим числом компонент. Кластеризация или квантование (b) позволяет снизить разнообразие данных, уменьшая число бит, требуемых для описания данных.

Возможно также объединение обоих типов кодирования. Например, очень богат приложениями метод топографических карт (или самоорганизующихся карт Кохонена - по имени предложившего их финского ученого), когда сами прототипы упорядочены в пространстве низкой размерности. Например, входные данные можно отобразить на упорядоченную двумерную сеть прототипов так, что появляется возможность визуализации многомерных данных.

Как и в случае с персептронами начать изучение нового типа обучения лучше с простейшей сети, состоящей из одного нейрона.

Нейрон - индикатор

Рассмотрим какие возможности по адаптивной обработке данных имеет единичный нейрон, и как можно сформулировать правила его обучения. В силу локальности нейросетевых алгоритмов, это базовое правило можно будет потом легко распространить и на сети из многих нейронов.

 

Постановка задачи

В простейшей постановке нейрон с одним выходом и d входами обучается на наборе d-мерных данных . В этой главе мы сосредоточимся, в основном, на обучении однослойных сетей, для которых нелинейность функции активации не принципиальна. Поэтому можно упростить рассмотрение, ограничившись линейной функции активации. Выход такого нейрона является линейной комбинацией его входов:

.

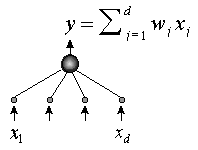
Рисунок 13. Сжатие информации линейным нейроном

Амплитуда этого выхода после соответствующего обучения (т.е. выбора весов по набору примеров ) может служить индикатором того, насколько данный вход соответствует обучающей выборке. Иными словами, нейрон может стать индикатором принадлежности входной информации к заданной группе примеров.

 

Правило обучения Хебба

Правило обучения отдельного нейрона-индикатора по-необходимости локально, т.е. базируется только на информации непосредственно доступной самому нейрону - значениях его входов и выхода. Это правило, носящее имя канадского ученого Хебба, играет фундаментальную роль в нейрокомпьютинге, ибо содержит как в зародыше основные свойства самоорганизации нейронных сетей.

Согласно Хеббу (Hebb, 1949), изменение весов нейрона при предъявлении ему -го примера пропорционально его входам и выходу:

, или в векторном виде: .

 

Если сформулировать обучение как задачу оптимизации, мы увидим, что обучающийся по Хеббу нейрон стремится увеличить амплитуду своего выхода:

,

 

где усреднение проводится по обучающей выборке . Вспомним, что обучение с учителем, напротив, базировалось на идее уменьшения среднего квадрата отклонения от эталона, чему соответствует знак минус в обучении по дельта-правилу. В отсутствие эталона минимизировать нечего: минимизация амплитуды выхода привела бы лишь к уменьшению чувствительности выходов к значениям входов. Максимизация амплитуды, напротив, делает нейрон как можно более чувствительным к различиям входной информации, т.е. превращает его в полезный индикатор.

Указанное различие в целях обучения носит принципиальный характер, т.к. минимум ошибки в данном случае отсутствует. Поэтому обучение по Хеббу в том виде, в каком оно описано выше, на практике не применимо, т.к. приводит к неограниченному возрастанию амплитуды весов.

 

Правило обучения Ойа

От этого недостатка, однако, можно довольно просто избавиться, добавив член, препятствующий возрастанию весов. Так, правило обучения Ойа:

, или в векторном виде: ,

 

максимизирует чувствительность выхода нейрона при ограниченной амплитуде весов. В этом легко убедиться, приравняв среднее изменение весов нулю. Умножив затем правую часть на , видим, что в равновесии: . Таким образом, веса обученного нейрона расположены на гипер-сфере: .

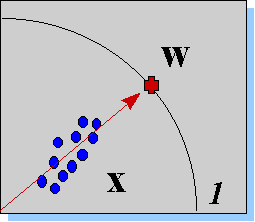
Рисунок 14. При обучении по Ойа, вектор весов нейрона располагается на гипер-сфере, в направлении, максимизирующем проекцию входных векторов.

Отметим, что это правило обучения по существу эквивалентно дельта-правилу, только обращенному назад - от входов к выходам (т.е. при замене ). Нейрон как бы старается воспроизвести значения своих входов по заданному выходу. Тем самым, такое обучение стремится максимально повысить чувствительность единственного выхода-индикатора к многомерной входной информации, являя собой пример оптимального сжатия информации.

Эту же ситуацию можно описать и по-другому. Представим себе персептрон с одним (здесь - линейным) нейроном на скрытом слое, в котором число входов и выходов совпадает, причем веса с одинаковыми индексами в обоих слоях одинаковы. Будем учить этот персептрон воспроизводить в выходном слое значения своих выходов. При этом, дельта-правило обучения верхнего (а тем самым и нижнего) слоя примет вид правила Ойа:

.

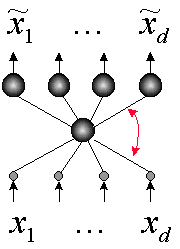
Рисунок 15. Автоассоциативная сеть с узким горлом - аналог правила обучения Ойа

Таким образом, существует определенная параллель между самообучающимися сетями и т.н. автоассоциативными сетями, в которых учителем для выходов являются значения входов. Подобного рода нейросети с узким горлом также способны осуществлять сжатие информации.

Взаимодействие нейронов: анализ главных компонент

Единственный нейрон осуществляет предельное сжатие многомерной информации, выделяя лишь одну скалярную характеристику многомерных данных. Каким бы оптимальным ни было сжатие информации, редко когда удается полностью охарактеризовать многомерные данные всего одним признаком. Однако, наращиванием числа нейронов можно увеличить выходную информацию. В этом разделе мы обобщим найденное ранее правило обучения на случай нескольких нейронов в самообучающемся слое, опираясь на отмеченную выше аналогию с автоассоциативными сетями.

 

Постановка задачи

Итак, пусть теперь на том же наборе d-мерных данных обучается m линейных нейронов:

.

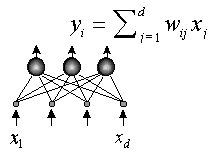
Рисунок 16. Слой линейных нейронов

Мы хотим, чтобы амплитуды выходных нейронов были набором независимых индикаторов, максимально полно отражающих информацию о многомерном входе сети.

 

Необходимость взаимодействия нейронов

Если мы просто поместим несколько нейронов в выходной слой и будем обучать каждый из них независимо от других, мы добьемся лишь многократного дублирования одного и того же выхода. Очевидно, что для получения нескольких содержательных признаков на выходе исходное правило обучения должно быть каким-то образом модифицировано - за счет включения взаимодействия между нейронами.

 

Самообучающийся слой

В нашей трактовке правила обучения отдельного нейрона, последний пытается воспроизвести значения своих входов по амплитуде своего выхода. Обобщая это наблюдение, логично было бы предложить правило, по которому значения входов восстанавливаются по всей выходой информации. Следуя этой линии рассуждений получаем правило Ойа для однослойной сети:

,

 

или в векторном виде: .

 

Такое обучение эквивалентно сети с узким горлом из скрытых линейных нейронов, обученной воспроизводитьна выходе значения своих входов.

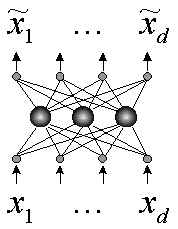
Рисунок 17. Автоассоциативная сеть с узким горлом - аналог правила обучения Ойа

Скрытый слой такой сети, так же как и слой Ойа, осуществляет оптимальное кодирование входных данных, и содержит максимально возможное при данных ограничениях количество информации.

 

Сравнение с традиционным статистическим анализом

Вывод о способности нейронных сетей самостоятельно выделять наиболее значимые признаки в потоках информации, обучаясь по очень простым локальным правилам, важен с общенаучной точки зрения. Изучение этих механизмов помогает глубже понять как функционирует мозг. Однако есть ли в описанных выше нейроалгоритмах какой-нибудь практический смысл?

Действительно, для этих целей существуют хорошо известные алгоритмы стандартного статистического анализа. В частности, анализ главных компонент также выделяет основные признаки, осуществляя оптимальное линейное сжатие информации. Более того, можно показать, что сжатие информации слоем Ойа эквивалентно анализу главных компонент. Это и не удивительно, поскольку оба метода оптимальны при одних и тех же ограничениях.

Однако стандартный анализ главных компонент дает решение в явном виде, через последовательность матричных операций, а не итерационно, как в случае нейросетевых алгоритмов. Так что при отсутствии высокопараллельных нейроускорителей на практике удобнее пользоваться матричными методами, а не обучать нейросети. Есть ли тогда практический смысл в изложенных выше итеративных нейросетевых алгоритмах?

Конечно же есть, по крайней мере по двум причинам:

  Во-первых, иногда обучение необходимо проводить в режиме on-line, т.е. на ходу адаптироваться к меняющемуся потоку данных. Примером может служить борьба с нестационарными помехами в каналах связи. Итерационные методы идеально подходят в этой ситуации, когда нет возможности собрать воедино весь набор примеров и произвести необходимые матричные операции над ним.

  Во-вторых, и это, видимо, главное, нейроалгоритмы легко обобщаются на случай нелинейного сжатия информации, когда никаких явных решений уже не существует. Никто не мешает нам заменить линейные нейроны в описанных выше сетях - нелинейными. С минимальными видоизменениями нейроалгоритмы будут работать и в этом случае, всегда находя оптимальное сжатие при наложенных нами ограничениях. Таким образом, нейроалгоритмы представляют собой удобный инструмент нелинейного анализа, позволяющий относительно легко находить способы глубокого сжатия информации и выделения нетривиальных признаков.

Иногда,даже простая замена линейной функции активации нейронов на сигмоидную в найденном выше правиле обучения:

 

приводит к новому качеству (Oja, et al, 1991). Такой алгоритм, в частности, с успехом применялся для разделения смешанных неизвестным образом сигналов (т.н. blind signal separation). Эту задачу каждый из нас вынужден решать, когда хочет выделить речь одного человека в шуме общего разговора.

Однако нас здесь интересуют не конкретные алгоритмы, а, скорее, общие принципы выделения значимых признаков, на которых имеет смысл остановиться несколько более подробно.

Соревнование нейронов: кластеризация

В начале данной главы мы упомянули два главных способа уменьшения избыточности: снижение размерности данных и уменьшение их разнообразия при той же размерности. До сих пор речь шла о первом способе. Обратимся теперь к второму. Этот способ подразумевает другие правила обучения нейронов.

 

Победитель забирает все

В Хеббовском и производных от него алгоритмах обучения активность выходных нейронов стремится быть по возможности более независимой друг от друга. Напротив, в соревновательном обучении, к рассмотрению которого мы приступаем, выходы сети максимально скоррелированы: при любом значении входа активность всех нейронов, кроме т.н. нейрона-победителя одинакова и равна нулю. Такой режим функционирования сети называется победитель забирает все.

 

Нейрон-победитель (с индексом ), свой для каждого входного вектора, будет служить прототипом этого вектора. Поэтому победитель выбирается так, что его вектор весов , определенный в том же -мерном пространстве, находится ближе к данному входному вектору , чем у всех остальных нейронов : для всех . Если, как это обычно и делается (вспомним слой Ойа), применять правила обучения нейронов, обеспечивающие одинаковую нормировку всех весов, например, , то победителем окажется нейрон, дающий наибольший отклик на данный входной стимул: . Выход такого нейрона усиливается до единичного, а остальных - подавляется до нуля.

Количество нейронов в соревновательном слое определяет максимальное разнообразие выходов и выбирается в соответствии с требуемой степенью детализации входной информации. Обученная сеть может затем классифицировать входы: нейрон-победитель определяет к какому классу относится данный входной вектор.

В отличае от обучения с учителем, самообучение не предполагает априорного задания структуры классов. Входные векторы должны быть разбиты по категориям (кластерам) согласуясь с внутренними закономерностями самих данных. В этом и состоит задача обучения соревновательного слоя нейронов.

 

Алгоритм обучения соревновательного слоя нейронов

Базовый алгоритм обучения соревновательного слоя остается неизменым:

,

 

поскольку задача сети также осталась прежней - как можно точнее отразить входную информацию в выходах сети. Отличае появляется лишь из-за нового способа кодирования выходной информации. В соревновательном слое лишь один нейрон - победитель имеет ненулевой (единичный) выход. Соответственно, в согласии с выписанным выше правилом, лишь его веса корректируются по предъявлении данного примера, причем для победителя правило обучения имеет вид:

.

 

Описанный выше базовый алгоритм обучения на практике обычно несколько модифицируют, т.к. он, например, допускает существование т.н. мертвых нейронов, которые никогда не выигрывают, и, следовательно, бесполезны. Самый простой способ избежать их появления - выбирать в качестве начальных значений весов случайно выбранные в обучающей выборке входные вектора.

Такой способ хорош еще и тем, что при достаточно большом числе прототипов он способствует равной "нагрузке" всех нейронов-прототипов. Это соответствует максимизации энтропии выходов в случае соревновательного слоя. В идеале каждый из нейронов соревновательного слоя должен одинаково часто становились победителем, чтобы априори невозможно было бы предсказать какой из них победит при случайном выборе входного вектора из обучающей выборки.

Наиболее быструю сходимость обеспечивает пакетный (batch) режим обучения, когда веса изменяются лишь после предъявления всех примеров. В этом случае можно сделать приращения не малыми, помещая вес нейрона на следующем шаге сразу в центр тяжести всех входных векторов, относящихся к его ячейке. Такой алгоритм сходится за итераций.

 

Кластеризация и квантование

Записав правило соревновательного обучения в градиентном виде: , легко убедиться, что оно минимизирует квадратичное отклонение входных векторов от их прототипов - весов нейронов-победителей:

.

 

Иными словами, сеть осуществляет кластеризацию данных: находит такие усредненные прототипы, которые минимизируют ошибку огрубления данных. Недостаток такого варианта кластеризации очевиден - "навязывание" количества кластеров, равного числу нейронов. В идеале сеть сама должна находить число кластеров, соответствующее реальной кластеризации векторов в обучающей выборке. Адаптивный подбор числа нейронов осуществляют несколько более сложные алгоритмы, такие, например, как растущий нейронный газ.

 

Идея последнего подхода состоит в последовательном увеличении числа нейронов-прототипов путем их "деления". Общую ошибку сети можно записать как сумму индивидуальных ошибок каждого нейрона:

.

 

Естественно предположить, что наибольшую ошибку будут иметь нейроны, окруженные слишком большим числом примеров и/или имеющие слишком большую ячейку. Такие нейроны и являются, в первую очередь, кандидатами на "почкование" (см. Рисунок 18).

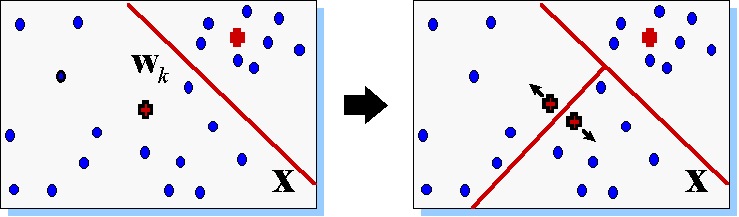
Рисунок 18. Деление нейрона с максимальной ошибкой в "растущем нейронном газе".

Соревновательные слои нейронов широко используются для квантования данных (vector quantization), отличающегося от кластеризации лишь большим числом прототипов. Это весьма распространенный на практике метод сжатия данных. При достаточно большом числе прототипов, плотность распределения весов соревновательного слоя хорошо аппроксимирует реальную плотность распределения многомерных входных векторов. Входное пространство разбивается на ячейки, содержащие вектора, относящиеся к одному и тому же прототипу. Причем эти ячейки (называемые ячейками Дирихле или ячейками Вороного) содержат примерно одинаковое количество обучающих примеров. Тем самым одновременно минимизируется ошибка огрубления и максимизируется выходная информация - за счет равномерной загрузки нейронов.

 

Сжатие данных в этом случае достигается за счет того, что каждый прототип можно закодировать меньшим числом бит, чем соответствующие ему вектора данных. При наличии прототипов для идентификации любого из них достаточно лишь бит, вместо бит описывающих произвольный входной вектор.

 

Оценка вычислительной сложности обучения

В этой главе мы рассмотрели два разных типа обучения, основанные на разных принципах кодирования информации выходным слоем нейронов. Логично теперь сравнить их по степени вычислительной сложности и выяснить когда выгоднее применять понижение размерности, а когда - квантование входной информации.

Как мы видели, алгоритм обучения сетей, понижающих размерность, сводится к обычному обучению с учителем, сложность которого была оценена ранее. Такое обучение требует операций, где - число синаптических весов сети, а - число обучающих примеров. Для однослойной сети с входами и выходными нейронами число весов равно и сложность обучения можно оценить как , где - коэффициент сжатия информации.

Кластеризация или квантование требуют настройки гораздо большего количества весов - из-за неэффективного способа кодирования. Зато такое избыточное кодирование упрощает алгоритм обучения. Действительно, квадратичная функция ошибки в этом случае диагональна, и в принципе достижение минимума возможно за шагов (например в пакетном режиме), что в данном случае потребует операций. Число весов, как и прежде, равно , но степень сжатия информации в данном случае определяется по-другому: . Сложность обучения как функция степени сжатия запишется в виде: .

 

При одинаковой степени сжатия, отношение сложности квантования к сложности данных снижения размерности запишется в виде:

.

 

Рисунок 19 показывает области параметров, при которых выгоднее применять тот или иной способ сжатия информации.

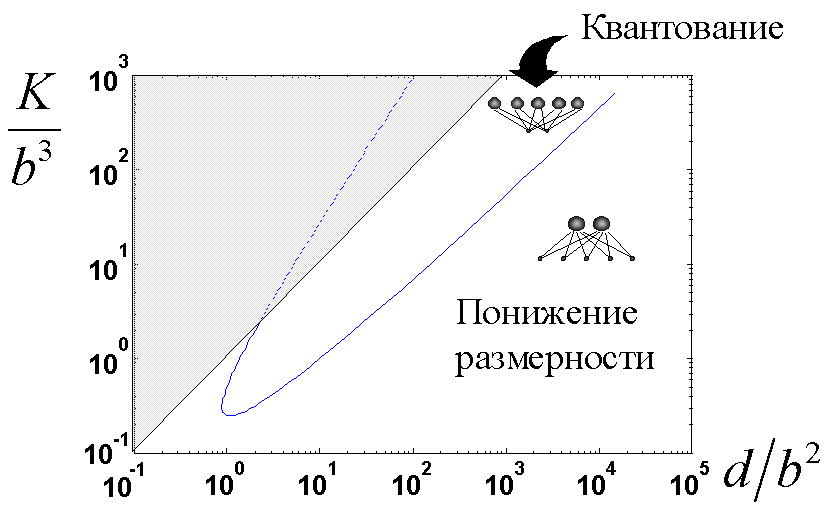
Рисунок 19. Области, где выгоднее использовать понижение размерности или квантование.

Наибольшее сжатие возможно методом квантования, но из-за экспоненциального роста числа кластеров, при большой размерности данных выгоднее использовать понижение размерности. Максимальное сжатие при понижении размерности равно , тогда как квантованием можно достичь сжатия (при двух нейронах-прототипах). Область недостижимых сжатий показана на рисунке серым.

В качестве примера рассмотрим типичные параметры сжатия изображений в формате JPEG. При этом способе сжатия изображение разбивается на квадраты со стороной 8x8 пикселей, которые и являются входными векторами, подлежащими сжатию. Следовательно, в данном случае . Предположим, что картинка содержит градаций серого цвета, т.е. точность представления данных . Тогда координата абсциссы на приведенном выше графике будет . Как следует из графика при любых допустимых степенях сжатия в данном случае оптимальным с точки зрения вычислительных затрат является снижение размерности.

Однако, при увеличении размеров элементарного блока, появляется область высоких степеней сжатия, достижимых лишь с использованием квантования. Скажем, при , когда , в соответствии с графиком (см. Рисунок 19), квантование следует применять для сжатия более , т.е. .

 

Победитель забирает не все

Один из вариантов модификации базового правила обучения соревновательного слоя состоит в том, чтобы обучать не только нейрон-победитель, но и его "соседи", хотя и с меньшей скоростью. Такой подход - "подтягивание" ближайших к победителю нейронов - применяется в топографических картах Кохонена. В силу большой практической значимости этой нейросетевой архитектуры, остановимся на ней более подробно.

Упорядочение нейронов: топографические карты

До сих пор нейроны выходного слоя были неупорядочены: положение нейрона-победителя в соревновательном слое не имело ничего общего с координатами его весов во входном пространстве. Оказывается, что небольшой модификацией соревновательного обучения можно добиться того, что положение нейрона в выходном слое будет коррелировать с положением прототипов в многомерном пространстве входов сети: близким нейронам будут соответствовать близкие значения входов. Тем самым, появляется возможность строить топографические карты чрезвычайно полезные для визуализации многомерной информации. Обычно для этого используют соревновательные слои в виде двумерных сеток. Такой подход сочетает квантование данных с отображением, понижающим размерность. Причем это достигается с помощью всего лишь одного слоя нейронов, что существенно облегчает обучение.

 

Алгоритм Кохонена

В 1982 году финский ученый Тойво Кохонен (Kohonen, 1982) предложил ввести в базовое правило соревновательного обучения информацию о расположении нейронов в выходном слое. Для этого нейроны выходного слоя упорядочиваются, образуя одно- или двумерные решетки. Т.е. теперь положение нейронов в такой решетке маркируется векторным индексом . Такое упорядочение естественым образом вводит расстояние между нейронами в слое. Модифицированное Кохоненым правило соревновательного обучения учитывает расстояние нейронов от нейрона-победителя:

.

 

Функция соседства равна единице для нейрона-победителя с индексом и постепенно спадает с расстоянием, например по закону . Как темп обучения , так и радиус взаимодействия нейронов постепенно уменьшаются в процессе обучения, так что на конечной стадии обучения мы возвращаемся к базовому правилу адаптации весов только нейронов-победителей.

В отличае от "газо-подобной" динамике обучения при индивидуальной подстройке прототипов (весов нейронов), обучение по Кохонену напоминает натягивание эластичной сетки прототипов на массив данных из обучающей выборки. По мере обучения эластичность сети постепенно увеличивается, чтобы не мешать окончательной тонкой подстройке весов.

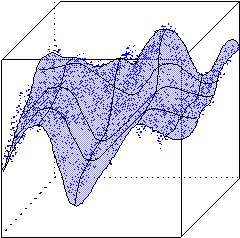
Рисунок 20. Двумерная топографическая карта набора трехмерных данных. Каждая точка в трехмерном пространстве попадает в свою ячейку сетки имеющую координату ближайшего к ней нейрона из двумерной карты.

В результате такого обучения мы получаем не только квантование входов, но и упорядочивание входной информации в виде одно- или двумерной карты. Каждый многомерный вектор имеет свою координату на этой сетке, причем чем ближе координаты двух векторов на карте, тем ближе они и в исходном пространстве. Такая топографическая карта дает наглядное представление о структуре данных в многомерном входном пространстве, геометрию которого мы не в состоянии представить себе иным способом. Визуализация многомерной информации является главным применением карт Кохонена.

Заметим, что в согласии с общим житейским принципом "бесплатных обедов не бывает", топографические карты сохраняют отношение близости лишь локально: близкие на карте области близки и в исходном пространстве, но не наоборот (Рисунок 21). В общем случае не существует отображения, понижающего размерность и сохраняющего отношения близости глобально.

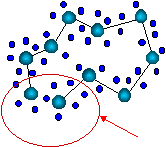
Рисунок 21. Пример одномерной карты двумерных данных. Стрелкой показана область нарушения непрерывности отображения: близкие на плоскости точки отображаются на противоположные концы карты

Удобным инструментом визуализации данных является раскраска топографических карт, аналогично тому, как это делают на обычных географических картах. Каждый признак данных порождает свою раскраску ячеек карты - по величине среднего значения этого признака у данных, попавших в данную ячейку.

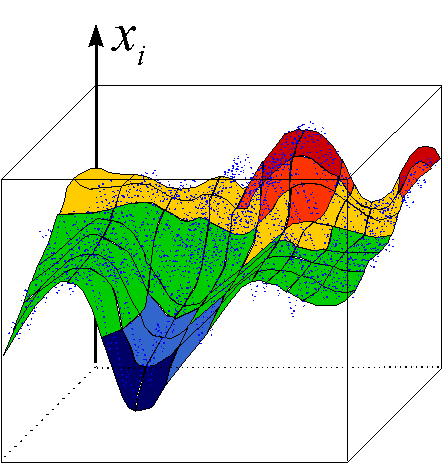
Рисунок 22. Раскраска топографической карты, индуцированная i-ой компонентой входных данных.

Собрав воедино карты всех интересующих нас признаков, получим топографический атлас, дающий интегральное представление о структуре многомерных данных. Далее в этой книге мы рассмотрим практическое применение этой методики к анализу балансовых отчетов и предсказанию банкротств.

Сети радиального базиса

Самообучающиеся сети, рассмотренные в этой главе, широко используются для предобработки данных, например при распознавании образов в пространстве очень большой размерности. В этом случае для того, чтобы процедура обучения с учителем была эффективна, требуется сначала сжать входную информацию тем или иным способом: либо выделить значимые признаки, понизив размерность, либо произвести квантование данных. Первый путь просто понижает число входов персептрона. Второй же способ требует отдельного рассмотрения, поскольку лежит в основе очень популярной архитектуры - сетей радиального базиса (radial basis functions - RBF).

 

Аппроксиматоры с локальным базисом

Сеть радиального базиса напоминают персептрон с одним скрытым слоем, осуществляя нелинейное отображение : , являющееся линейной комбинацией базисных функций. Но в отличие от персептронов, где эти функции зависили от проекций на набор гиперплоскостей , в сетях радиального базиса используются функции (чаще всего - гауссовы), зависящие от расстояний до опорных центров:

.

 

Как тот, так и другой набор базисных функций обеспечивают возможность аппроксимации любой непрерывной функции с произвольной точностью. Основное различие между ними в способе кодирования информации на скрытом слое. Если персепторны используют глобальные переменные (наборы бесконечных гиперплоскостей), то сети радиального базиса опираются на компактные шары, окружающие набор опорных центров (Рисунок 23).

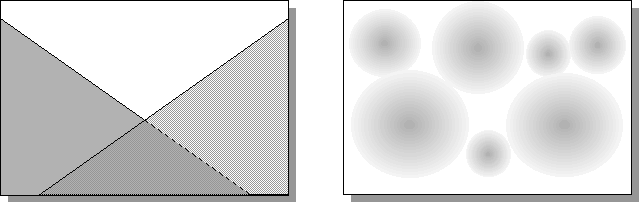
Рисунок 23. Глобальная (персептроны) и локальная (сети радиального базиса) методы аппроксимации

В первом случае в аппроксимации в окрестности любой точки участвуют все нейроны скрытого слоя, во втором - лишь ближайшие. Как следствие такой неэффективности, в последнем случае количество опорных функций, необходимых для аппроксимации с заданной точностью, возрастает экспоненциально с размерностью пространства. Это основной недостаток сетей радиального базиса. Основное же их преимущество над персептронами - в простоте обучения.

 

Гибридное обучение

Относительная автономность базисных функций позволяет разделить обучение на два этапа. На первом этапе обучается первый - соревновательный - слой сети, осуществляя квантование данных. На втором этапе происходит быстрое обучение второго слоя матричными методами, т.к. нахождение коэффициентов второго слоя представляет собой линейную задачу.

Подобная возможность раздельного обучения слоев является основным достоинством сетей радиального базиса. В целом же, области применимости персептронов и сетей радиального базиса коррелируют с найденными выше областями эффективности квантования и понижения размерности (см. Рисунок 19).

 

Выводы

В этой главе мы познакомились со вторым из двух главных типов обучения - обучением без учителя. Этот режим обучения чрезвычайно полезен для предобработки больших массивов информации, когда получить экспертные оценки для обучения с учителем не представляется возможным. Самообучающиеся сети способны выделять оптимальные признаки, формируя относительно малоразмерное пространство признаков, без чего иногда невозможно качественное распознавание образов. Таким образом, оба типа обучения удачно дополняют друг друга. Кроме того, как мы убедились на примере сетей с узким горлом, между этими типами обучения существует тесная взаимосвязь: если посмотреть на ситуацию под определенным углом зрения, соответствующие правила обучения подчас просто совпадают.