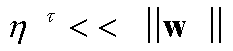Лекция 2. Обучение с учителем: Распознавание образов

Персептроны. Прототипы задач

Сети, о которых пойдет речь в этой главе, являются основной "рабочей лошадкой" современного нейрокомпьютинга. Подавляющее большинство приложений связано именно с применением таких многослойных персептронов или для краткости просто персептронов (напомним, что это название происходит от английского perception - восприятие, т.к. первый образец такого рода машин предназначался как раз для моделирования зрения). Как правило, используются именно сети, состоящие из последовательных слоев нейронов. Хотя любую сеть без обратных связей можно представить в виде последовательных слоев, именно наличие многих нейронов в каждом слое позволяет существенно ускорить вычисления используя матричные ускорители.

В немалой степени популярность персептронов обусловлена широким кругом доступных им задач. В общем виде они решают задачу аппроксимации многомерных функций, т.е. построения многомерного отображения , обобщающего заданный набор примеров .

В зависимости от типа выходных переменных (тип входных не имеет решающего значения), аппроксимация функций может принимать вид

  Классификации (дискретный набор выходных значений), или

  Регрессии (непрерывные выходные значения)

Многие практические задачи распознавания образов, фильтрации шумов, предсказания временных рядов и др. сводится к этим базовым прототипическим постановкам.

Причина популярности персептронов кроется в том, что для своего круга задач они являются во-первых универсальными, а во-вторых - эффективными с точки зрения вычислительной сложности устройствами. В этой главе мы затронем оба аспекта.

Возможности многослойных персептронов

Изучение возможностей многослойных персептронов удобнее начать со свойств его основного компонента и одновременно простейшего персептрона - отдельного нейрона.

Нейрон - классификатор

Простейшим устройством распознавания образов, принадлежащим к рассматриваемому классу сетей, является одиночный нейрон, превращающий входной вектор признаков в скалярный ответ, зависящий от линейной комбинации входных переменных:

Здесь и далее мы предполагаем наличие у каждого нейрона дополнительного единичного входа с нулевым индексом, значение которого постоянно: . Это позволит упростить выражения, трактуя все синаптические веса , включая порог , единым образом.

Скалярный выход нейрона можно использовать в качестве т.н. дискриминантной функции. Этим термином в теории распознавания образов называют индикатор принадлежности входного вектора к одному из заданных классов. Так, если входные векторы могут принадлежать одному из двух классов, нейрон способен различить тип входа, например, следующим образом: если , входной вектор принадлежит первому классу, в противном случае - второму.

Поскольку дискриминантная функция зависит лишь от линейной комбинации входов, нейрон является линейным дискриминатором. В некоторых простейших ситуациях линейный дискриминатор - наилучший из возможных, а именно - в случае когда вероятности принадлежности входных векторов к классу k задаются гауссовыми распределениями с одинаковыми ковариационными матрицами . В этом случае границы, разделяющие области, где вероятность одного класса больше, чем вероятность остальных, состоят из гиперплоскостей (см. Рисунок 4 иллюстрирующий случай двух классов).

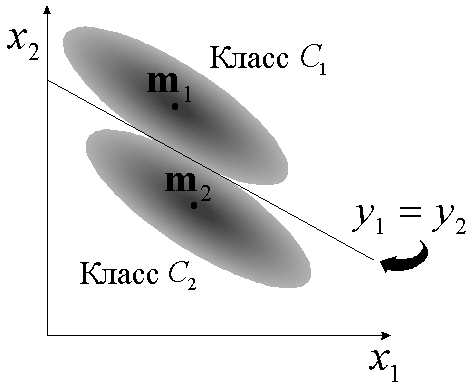
Рисунок 4. Линейный дискриминатор дает точное решение в случае если вероятности принадлежности к различным классам - гауссовы, с одинаковым разбросом и разными центрами в пространстве параметров.

 

В более общем случае поверхности раздела между классами можно описывать приближенно набором гиперплоскостей - но для этого уже потребуется несколько линейных дискриминаторов - нейронов.

Выбор функции активации

Монотонные функции активации не влияют на классификацию. Но их значимость можно повысить, выбрав таким образом, чтобы можно было трактовать выходы нейронов как вероятности принадлежности к соответствующему классу, что дает дополнительную информацию при классификации. Так, можно показать, что в упомянутом выше случае гауссовых распределений вероятности, сигмоидная функция активации нейрона дает вероятность принадлежности к соответствующему классу.

Двухслойные персептроны

Возможности линейного дискриминатора весьма ограничены. Он способен правильно решать лишь ограниченный круг задач - когда классы, подлежащие классификации линейно-разделимы, т.е. могут быть разделены гиперплоскостью (Рисунок 5).

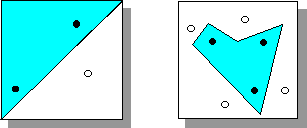
Рисунок 5. Пример линейно разделимых (слева) и линейно-неразделимых (справа) множеств

 

В d-мерном пространстве гиперплоскость может разделить произвольным образом лишь d+1 точки. Например, на плоскости можно произвольным образом разделить по двум классам три точки, но четыре - в общем случае уже невозможно (см. Рисунок 5). В случае плоскости это очевидно из приведенного примера, для большего числа измерений - следует из простых комбинаторных соображений. Если точек больше чем d+1 всегда существуют такие способы их разбиения по двум классам, которые нельзя осуществить с помощью одной гиперплоскости. Однако, этого можно достичь с помощью нескольких гиперплоскостей.

Для решения таких более сложных классификационных задач необходимо усложнить сеть, вводя дополнительные (их называют скрытыми) слои нейронов, производящих промежуточную предобработку входных данных таким образом, чтобы выходной нейрон-классификатор получал на свои входы уже линейно-разделимые множества.

Причем легко показать, что, в принципе, всегда можно обойтись всего лишь одним скрытым слоем, содержащим достаточно большое число нейронов. Действительно, увеличение скрытого слоя повышает размерность пространства, в котором выходной нейрон производит дихотомию, что, как отмечалось выше, облегчает его задачу.

Не вдаваясь в излишние подробности резюмируем результаты многих исследований аппроксимирующих способностей персептронов.

  Сеть с одним скрытым слоем, содержащим H нейронов со ступенчатой функцией активации, способна осуществить произвольную классификацию Hd точек d-мерного пространства (т.е. классифицмровать Hd примеров).

  Одного скрытого слоя нейронов с сигмоидной функцией активации достаточно для аппроксимации любой границы между классами со сколь угодно высокой точностью.

Для задач аппроксимации последний результат переформулируется следующим образом:

  Одного скрытого слоя нейронов с сигмоидной функцией активации достаточно для аппроксимации любой функции со сколь угодно высокой точностью. (Более того, такая сеть может одновременно аппроксимировать и саму функцию и ее производные.)

Точность аппроксимации возрастает с числом нейронов скрытого слоя. При нейронах ошибка оценивается как . Эта оценка понадобится нам в дальнейшем.

Градиентное обучение многослойных персептронов

Градиентное обучение

Наиболее общим способом оптимизации нейросети является итерационная (постепенная) процедура подбора весов, называемая обучением, в данном случае - обучением с учителем, поскольку опирается на обучающую выборку примеров , например - примеров правильной классификации.

Когда функционал ошибки задан, и задача сводится к его минимизации, можно предложить, например, следующую итерационную процедуру подбора весов: или, что то же самое: .

Здесь - темп обучения на шаге . Можно показать, что постепенно уменьшая темп обучения, например по закону , описанная выше процедура приводит к нахождению локального минимума ошибки.

Исторически наибольшую трудность на пути к эффективному правилу обучения многослойных персептронов вызвала процедура эффективного расчета градиента функции ошибки. Дело в том, что ошибка сети определяется по ее выходам, т.е. непосредственно связаня лишь с выходным слоем весов. Вопрос состоял в том, как определить ошибку для нейронов на скрытых слоях, чтобы найти производные по соответствующим весам. Нужна была процедура передачи ошибки с выходного слоя к предшествующим слоям сети, в направлении обратном обработке входной информации. Поэтому такой метод, когда он был найден, получил название метода обратного распространения ошибки.

Метод обратного распространения ошибки

Ключ к обучению многослойных персептронов оказался настолько простым и очевидным, что, как оказалось, неоднократно переоткрывался.

  Так, например, базовый алгоритм был изложен в диссертации Пола Вербоса (Paul Werbos) 1974 года, но тогда не привлек к себе должного внимания. Рождение алгоритма back-propagation (обратного распространения ошибки) для широкой публики связано с работой группы PDP (Parallel Distributed Processing), освещенной в двухтомном труде 1986г. Именно там в статье Румельхарта, Хинтона и Уильямса была изложена теория обучения многослойного персептрона.

Между тем, в случае дифференцируемых функций активации рецепт нахождения производных по любому весу сети дается т.н. цепным правилом дифференцирования, известным любому первокурснику. Суть метода back-propagation - в эффективном воплощении этого правила.

  Фрэнк Розенблаттом использовал в своем персептроне недифференцируемую ступенчатую функцию активации. Возможно, именно это помешало ему найти эфективный алгоритм обучения, хотя сам термин Back Propagation восходит к его попыткам обобщить свое правило обучения одного нейрона на многослойную сеть. Как знать, используй Розенблатт вместо ступенчатой функции активации - сигмоидную, может быть его судьба сложилась бы по-другому.

Разберем этот ключевой для нейрокомпьютинга метод несколько подробнее. Обозначим входы n-го слоя нейронов . Нейроны этого слоя вычисляют соответствующие линейные комбинации:

и передают их на следующий слой, пропуская через нелинейную функцию активации (для простоты - одну и ту же, хотя это совсем необязательно):

.

Для построения алгоритма обучения нам надо знать производную ошибки по каждому из весов сети:

.

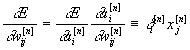Таким образом, вклад в общую ошибку каждого веса вычисляется локально, простым умножением невязки нейрона на значение соответствующего входа. (Из-за этого, в случае когда веса изменяют по направлению скорейшего спуска , такое правило обучения называют дельта-правилом.)

Входы каждого слоя вычисляются последовательно от первого слоя к последнему во время прямого распространения сигнала:

,

а невязки каждого слоя вычисляются во время обратного распространения ошибки от последнего слоя (где они определяются по выходам сети) к первому:

.

Последняя формула получена применением цепного правила к производной

и означает, что чем сильнее учитывается активация данного нейрона на следующем слое, тем больше его ответственность за общую ошибку.

Эффективность алгоритма back-propagation

Важность изложенного выше алгоритма back-propagation в том, что он дает чрезвычайно эффективный способ нахождения градиента функции ошибки. Если обозначить общее число весов в сети как , то необходимое для вычисления градиента число операций растет пропорционально , т.е. этот алгоритм имеет сложность . Напротив, прямое вычисление градиента по формуле

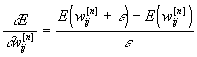
потребовала бы прямых прогонов через сеть, требующих операций каждый. Таким образом "наивный" алгоритм имеет сложность , что существенно хуже, чем у алгоритма back-propagation.

Использование алгоритма back-propagation

При оценке значения алгоритма back-propagation важно различать нахождение градиента ошибки и его использование для обучения. Иногда под этим именем понимают именно конкретный тип итерационного обучения, предложенный в статье Румельхарта с соавторами. Этот простейший тип обучения (метод скорейшего спуска) обладает рядом недостатков. Существуют много гораздо более хороших алгоритмов обучения, использующих градиент ошибки более эффективно. Ниже мы перечислим некоторые из них, наиболее часто используемые на практике. Подчеркнем, однако, что все они так или иначе используют изложенный выше метод back-propagation для нахождения градиента ошибки.

Итак, простейший способ использования градиента при обучении - изменение весов пропорционально градиенту - т.н метод наискорейшего спуска:

.

Этот метод оказывается, однако, чрезвычайно неэффективен в случае, когда производные по различным весам сильно отличаются, т.е. рельеф функции ошибки напоминает не яму, а длинный овраг. (Это соответствует ситуации, когда активация некоторых из сигмоидных нейронов близка по модулю к 1 или, что то же самое - когда модуль некоторых весов много больше 1). В этом случае для плавного уменьшения ошибки необходимо выбирать очень маленький темп обучения, диктуемый максимальной производной (шириной оврага), тогда как расстояние до минимума по порядку величины определяется минимальной производной (длиной оврага). В итоге обучение становится неприемлемо медленным. Кроме того, на самом дне оврага неизбежно возникают осцилляции, и обучение теряет привлекательное свойство монотонности убывания ошибки.

Рисунок 6. Неэффективность метода скорейшего спуска: градиент направлен не в сторону минимума

 

Простейшим усовершенствованием метода скорейшего спуска является введение момента , когда влияние градиента на изменение весов накапливается со временем:

.

Качественно влияние момента на процесс обучения можно пояснить следующим образом. Допустим, что градиент меняется плавно, так что на протяжении некоторого времени его изменением можно пренебречь (мы находимся далеко от дна оврага). Тогда изменение весов можно записать в виде:

,

т.е. в этом случае эффективный темп обучения увеличивается, причем существенно, если момент . Напротив, вблизи дна оврага, когда направление градиента то и дело меняет знак из-за описанных выше осцилляций, эффективный темп обучения замедляется до значения близкого к :

.

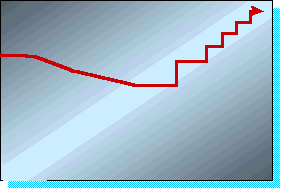
Рисунок 7. Введение инерции в алгоритм обучения позволяет адаптивно менять скорость обучения

 

Дополнительное преимущество от введения момента - появляющаяся у алгоритма способность преодолевать мелкие локальные минимумы. Это свойство можно увидеть, записав разностное уравнение для обучения в виде дифференциального. Тогда обучение методом скорейшего спуска будет описываться уравненем движения тела в вязкой среде: . Введение момента соответствует появлению у такого гипотетического тела инерции, т.е. массы : . В итоге, "разогнавшись", тело может по инерции преодолевать небольшие локальные минимумы ошибки, застревая лишь в относительно глубоких, значимых минимумах.

Одним из недостатков описанного метода является введение еще одного глобального настроечного параметра. Мы же, наоборот, должны стремиться к отсутствию таких навязываемых алгоритму извне параметров. Идеальной является ситуация, когда все параметры обучения сами настраиваются в процессе обучения, извлекая информацию о характере рельефа функции ошибки из самого хода обучения. Примером весьма удачного алгоритма обучения является т.н. RPROP (от resilient - эластичный), в котором каждый вес имеет свой адаптивно настраиваемый темп обучения.

RPROP стремится избежать замедления темпа обучения на плоских "равнинах" ландшафта функции ошибки, характерного для схем, где изменения весов пропорциональны величине градиента. Вместо этого RPROP использует лишь знаки частных производных по каждому весу.

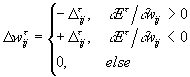
Величина шага обновления - своя для каждого веса и адаптируется в процессе обучения:

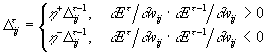
Если знак производной по данному весу изменил направление, значит предыдущее значение шага по данной координате было слишком велико, и алгоритм уменьшает его в раз. В противном случае шаг увеличивается в раз для ускорения обучения вдали от минимума.

Мы не затронули здесь более изощренных методов обучения, таких как метод сопряженного градиента, а также методов второго порядка, которые используют не только информацию о градиенте функции ошибки, но и информацию о вторых производных. Их разбор вряд ли уместен при первом кратком знакомстве с основами нейрокомпьютинга.

Вычислительная сложность обучения

Ранее при обсуждении истории нейрокомпьютинга мы ссылались на относительную трудоемкость процесса обучения. Чтобы иметь хотя бы приблизительное представление о связанных с обучением вычислительных затратах, приведем качественную оценку вычислительной сложности алгоритмов обучения.

Пусть как всегда - число синаптических весов сети (weights), а - число обучающих примеров (patterns). Тогда для однократного вычисления градиента функции ошибки требуется порядка операций. Допустим для простоты, что мы достаточно близки к искомому минимуму и можем вблизи этого минимума аппроксимировать функцию ошибки квадратичным выражением . Здесь - матрица вторых производных в точке минимума . Оценив эту матрицу по локальной информации (для чего потребуется операций метода back-propagation), можно попасть из любой точки в минимум за один шаг. На этой стратегии построены методы вторго порядка (метод Ньютона). Альтернативная стратегия - найти требуемые параметров за шагов метода первого порядка, затратив на каждом шаге операций. Именно такую скорость сходимости ( итераций) имеют лучшие алгоритмы первого порядка (например, метод сопряженного градиента). В обоих случаях оптимистическая оценка сложности обучения сети (т.к. она получена для простейшего из всех возможных - квадратичного - рельефа) составляет операций.

Оптимизация размеров сети

В описанных до сих пор методах обучения значения весов подбиралось в сети с заданной топологией связей. А как выбирать саму структуру сети: число слоев и количество нейронов в этих слоях? Решающим, как мы увидим, является выбор соотношения между числом весов и числом примеров. Зададимся поэтому теперь следующим вопросом:

  Как связаны между собой число примеров и число весов в сети ?

Ошибка аппроксимации

Рассмотрим для определенности двухслойную сеть (т.е. сеть с одним скрытым слоем). Точность аппроксимации функций такой сетью, как уже говорилось, возрастает с числом нейронов скрытого слоя. При нейронах ошибка оценивается как . Поскольку число выходов сети не превышает, а как правило - много меньше числа входов, основное число весов в двухслойной сети сосредоточено в первом слое, т.е. . В этом случае средняя ошибка аппроксимации выразится через общее число весов в сети следующим образом:

.

где - размерность входов.

Наши недостатки, как известно - продолжения наших достоинств. И упомянутая выше универсальность персептронов превращается одновременно в одну из главных проблем обучающихся алгоритмов, известную как проблема переобучения.

Переобучение

Суть этой проблемы лучше всего объяснить на конкретном примере. Пусть обучающие примеры порождаются некоторой функцией, которую нам и хотелось бы воспроизвести. В теории обучения такую функцию называют учителем. При конечном числе обучающих примеров всегда возможно построить нейросеть с нулевой ошибкой обучения, т.е. ошибкой, определенной на множестве обучающих примеров. Для этого нужно взять сеть с числом весов большим, чем число примеров. Действительно, чтобы воспроизвести каждый пример у нас имеется уравнений для неизвестных. И если число неизвестных меньше числа уравнений, такая система является недоопределенной и допускает бесконечно много решений. В этом-то и состоит основная проблема: у нас не хватает информации, чтобы выбрать единственное правильное решение - функцию-учителя. В итоге выбранная случайным образом функция дает плохие предсказания на новых примерах, отсутствовавших в обучающей выборке, хотя последнюю сеть воспроизвела без ошибок. Вместо того, чтобы обобщить известные примеры, сеть запомнила их. Этот эффект и называется переобучением.

На самом деле, задачей теории обучения является не минимизация ошибки обучения, а минимизация ошибки обобщения, определенной для всех возможных в будущем примеров. Именно такая сеть будет обладать максимальной предсказательной способностью. И трудность здесь состоит в том, что реально наблюдаемой является именно и только ошибка обучения. Ошибку обобщения можно лишь оценить, опираясь на те или иные соображения.

В этой связи вспомним изложенный в начале этой главы принцип минимальной длины описания. Согласно этому общему принципу, ошибка предсказаний сети на новых данных определяется общей длиной описания данных с помощью модели вместе с описанием самой модели:

Первый член этого выражения отвечает наблюдаемой ошибке обучения. Мы оценили его выше. Теперь обратимся к оценке второго члена, регуляризирующего обучение.

Ошибка, связанная со сложностью модели

Описание сети сводится, в основном, к передаче значений ее весов. При заданной точности такое описание потребует порядка

бит. Следовательно, удельную ошибку на один пример, связанную со сложностью модели, можно оценить следующим образом:

.

Она, как мы видим, монотонно спадает с ростом числа примеров.

Действительно, для однозначного определения подгоночных параметров (весов сети) по заданным примерам необходимо, чтобы система уравнений была переопределена, т.е. число параметров было больше числа уравнений. Чем больше степень переопределенности, тем меньше результат обучения зависит от конкретного выбора подмножества обучающих примеров. Определенная выше составляющая ошибки обобщения, как раз и связана с вариациями решения, обусловленными конечностью числа примеров.

Оптимизация размера сети

Итак, мы оценили обе составляющих ошибки обобщения сети. Важно, что эти составляющие по-разному зависят от размера сети (числа весов), что предполагает возможность выбора оптимального размера, минимизирующего общую ошибку:

.

Минимум ошибки (знак равенства) достигается при оптимальном числе весов в сети

,

соответствующих числу нейронов в скрытом слое равному по порядку величины:

.

Этот результат можно теперь использовать для получения окончательной оценки сложности обучения ( - от английского complexity)

Отсюда можно сделать следующий практический вывод: нейроэмуляторам с производительностью современных персональных компьютеров ( операций в секунду) вполне доступны анализ баз данных с числом примеров и размерностью входов . Типичное время обучения при этом составит секунд, т.е. от десятков минут до несколько часов. Поскольку производственный цикл нейроанализа предполагает обучение нескольких, иногда - многих сетей, такой размер баз данных, представляется предельным для нейротехнологии на персональных компьютерах. Эти оценки поясняют также относительно позднее появление нейрокомпьютинга: для решения практически интересных задач требуется производительность суперкомпьютеров 70-х годов.

Согласно полученным выше оценкам ошибка классификации на таком классе задач порядка 10%. Это, конечно, не означает, что с такой точностью можно предсказывать что угодно. Многие относительно простые задачи классификации решаются с большей точностью, поскольку их эффективная размерность гораздо меньше, чем число входных переменных. Напротив, для рыночных котировок достижение соотношения правильных и неправильных предсказаний 65:35 уже можно считать удачей. Действительно, приведенные выше оценки предполагали отсутствие случайного шума в примерах. Шумовая составляющая ошибки предсказаний должна быть добавлена к полученной выше оценке. Для сильно зашумленных рыночных временных рядов именно она определяет предельную точность предсказаний. Подробнее эти вопросы будут освещены в отдельной главе, посвященной предсказанию зашумленных временных рядов.

Другой вывод из вышеприведенных качественных оценок - обязательность этапа предобработки высокоразмерных данных. Невозможно классифицировать непосредственно картинки с размерностью . Из оценки точности классификации следует, что это потребует числа обучающих примеров по крайней мере такого же порядка, т.е. сложность обучения будет порядка . Современным нейрокомпьютерам с производительностью операций в секунду потребовалось бы несколько лет обучения распознаванию таких образов. Зрительная система человека, составляющая несколько процентов коры головного мозга, т.е. обладающая производительностью способна обучаться распознаванию таких образов за несколько часов. В действительности, зрительный нерв содержит как раз около нервных волокон. Напомним, однако, что в сетчатке глаза содержится порядка клеток-рецепторов. Таким образом, уже в самом глазе происходит существенный этап предобработки исходного сигнала, и в мозг поступает уже такая информация, которую он способен усвоить. (Непосредственное распознавание образов с потребовало бы обучения на протяжении секунд, т.е. около 300 лет.)

Методы предобработки сигналов и формирования относительно малоразмерного пространства признаков являются важнейшей составляющей нейроанализа и будут подробно рассмотрены далее в отдельной главе.

Адаптивная оптимизации архитектуры сети

Итак, мы выяснили, что существует оптимальная сложность сети, зависящая от количества примеров, и даже получили оценку размеров скрытого слоя для двухслойных сетей. Однако в общем случае следует опираться не на грубые оценки, а на более надежные механизмы адаптации сложности нейросетевых моделей к данным для каждой конкретной задачи.

Для борьбы с переобучением в нейрокомпьютинге используются три основных подхода:

  Ранняя остановка обучения

  Прореживание связей (метод от большого - к малому)

  Поэтапное наращивание сети (от малого - к большому)

 

Валидация обучения

Прежде всего, для любого из перечисленных методов необходимо определить критерий оптимальной сложности сети - эмпирический метод оценки ошибки обобщения. Поскольку ошибка обобщения определена для данных, которые не входят в обучающее множество, очевидным решением проблемы служит разделение всех имеющихся в нашем распоряжении данных на два множества: обучающее - на котором подбираются конкретные значения весов, и валидационного - на котором оценивается предсказательные способности сети и выбирается оптимальная сложность модели. На самом деле, должно быть еще и третье - тестовое множество, которое вообще не влияет на обучение и используется лишь для оценки предсказательных возможностей уже обученной сети.

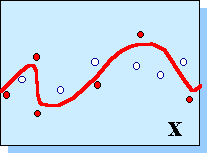
Рисунок 8. Обучающее (темные точки) и валидационные (светлые точки) множества примеров

 

Ранняя остановка обучения

Обучение сетей обычно начинается с малых случайных значений весов. Пока значения весов малы по сравнением с характерным масштабом нелинейной функции активации (обычно принимаемом равным единице), вся сеть представляет из себя суперпозицию линейных преобразований, т.е. является также линейным преобразованием с эффективным числом параметров равным числу входов, умноженному на число выходов. По мере возрастания весов и степень нелинейности, а вместе с ней и эффективное число параметров возрастает, пока не сравняется с общим числом весов в сети.

В методе ранней остановки обучение прекращается в момент, когда сложность сети достигнет оптимального значения. Этот момент оценивается по поведению во времени ошибки валидации. Рисунок 9 дает качественное представление об этой методике.

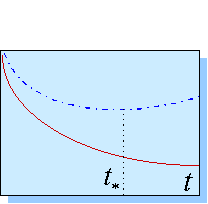
Рисунок 9. Ранняя остановка сети в момент минимума ошибки валидации (штрих-пунктирная кривая). При этом обычно ошибка обучения (сплошная кривая) продолжает понижаться.

 

Эта методика привлекательна своей простотой. Но она имеет и свои слабые стороны: слишком большая сеть будет останавливать свое обучение на ранних стадиях, когда нелинейности еще не успели проявиться в полную силу. Т.е. эта методика чревата нахождением слабо-нелинейных решений. На поиск сильно нелинейных решений нацелен метод прореживания весов, который, в отличае от предыдущего, эффективно подавляет именно малые значения весов.

Прореживание связей

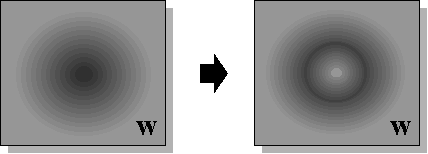
Эта методика стремится сократить разнообразие возможных конфигураций обученных нейросетей при минимальной потере их аппроксимирующих способностей. Для этого вместо колоколообразной формы априорной функции распределения весов, характерной для обычного обучения, когда веса "расползаются" из начала координат, применяется такой алгоритм обучения, при котором функция распределения весов сосредоточена в основном в "нелинейной" области относительно обльших значений весов (см. Рисунок 10).

Рисунок 10. Подавление малых значений весов в методе прореживания связей

 

Этого достигают введением соответствующей штрафной составляющей в функционал ошибки. Например, априорной функции распределения:

,

имеющую максимум в вершинах гиперкуба с , соответствует штрафной член:

в функционале ошибки. Дополнительная составляющая градиента

исчезающе мала для больших весов, , и пропорциональна величине малых весов, . Соответственно, на больших штрафная функция практически не сказывается, тогда как малые веса экспоненциально затухают.

Таким образом, происходит эффективное вымывание малых весов (weights elimination), т.е. прореживание малозначимых связей. Противоположная методика предполагает, напротив, поэтапное наращивание сложности сети. Соответствующее семейство алгоритмов обучения называют конструктивными алгоритмами.

Конструктивные алгоритмы

Эти алгоритмы характеризуются относительно быстрым темпом обучения, поскольку разделяют сложную задачу обучения большой многослойной сети на ряд более простых задач, обычно - обучения однослойных подсетей, составляющих большую сеть. Поскольку сложность обучения пропорциональна квадрату числа весов, обучение "по частям" выгоднее, чем обучение целого:

.

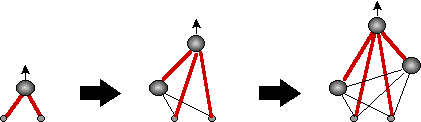
Для примера опишем так называемую каскад-корреляционную методику обучения нейросетей. Конструирование сети начинается с единственного выходного нейрона и происходит путем добавления каждый раз по одному промежуточному нейрону (см. Рисунок 11).

Рисунок 11. Каскад-корреляционные сети: добавление промежуточных нейронов с фиксированными весами.

 

Эти промежуточные нейроны имеют фиксированные веса, выбираемые таким образом, чтобы выход добавляемых нейронов в максимальной степени коррелировал с ошибками сети на данный момент (откуда и название таких сетей). Поскольку веса промежуточных нейронов после добавления не меняются, их выходы для каждого значения входов можно вычислить лишь однажды. Таким образом, каждый добавляемый нейрон можно трактовать как дополнительный признак входной информации, максимально полезный для уменьшения ошибки обучения на данном этапе роста сети. Оптимальная сложность сети может определяться, например, с помощью валидационного множества.