Глава 2. Плетение и закидывание сетей и неводов

 

2.1. Предобработка данных

 

Среди m признаков (которые иначе могут называться переменными) могут быть признаки, измеряемые в количественной, номинальной или порядковой шкалах. В самом простом случае все признаки измеряются в одной и той же шкале, но в реальных ситуациях, как правило, используются несколько типов шкал измерения признаков.

Перед применением к данным различных алгоритмов анализа их структуры всегда возникает необходимость применения различных способов предобработки, которая в задаче визуализации данных заключается в оцифровке, нормировке и выборе метрики.

 

2.1.1. Обозначения

 

Для того, чтобы последующее изложение было более ясным, введем систему обозначений, которой будем придерживаться на протяжении всей последующей главы.

X_i, Y_i – совокупность координат i-ой точки данных (радиус-вектор);

X_i×Y_i или (X_i ,Y_i)– скалярное произведение вектора X_i и Y_j;

(X_i)² – «квадрат вектора» – сумма квадратов его координат (число);

x_ij – значение j-ой координаты i-ой точки объекта (число);

x_i, h_i – обозначения i-ой координаты пространства данных (как меняющейся величины);

m – размерность пространства данных;

, N – число объектов;

d_ij – «дельта-символ» Кронеккера: .

 

2.1.2. Оцифровка дискретных шкал

 

Под оцифровкой, как правило, подразумевается приведение всех типов признаков к одной количественной шкале.

В самом простом случае дихотомической шкалы, то есть когда признак может принимать значения «да» или «нет», нет большой разницы какие числа будут приписаны положительному или отрицательному ответу. Самые распространенные варианты: ответу «да» приписывают число 1, ответу «нет» – либо –1, либо 0.

В случае порядковых шкал, как правило, порядок следования градаций признака отражает степень усиления или ослабления того или иного качества. Числовые метки признака в этом случае присваиваются таким образом, чтобы расстояния между двумя отметками интуитивно соответствовали разнице между соответствующими градациями (например, если признак имеет шкалу «плохо-никак-хорошо», то логично приписать градациям метки –1;0;1,  а вот в случае шкалы «малый-средний-крупный-сверхкрупный» более уместным может оказаться использовать логарифмические метки, т.е. 0.1;1;10;100). Не играет большого значения выбор «начала отсчета» шкалы признака, но психологически удобнее измерять в числовой шкале с отрицательными и положительными числовыми метками качество, меняющееся от противоположности к противоположности (как «плохо-хорошо»), а в шкалах с «абсолютным нулем» измерять постепенное нарастание какого-либо качества (как «отсутствие-частичное присутствие-полное присутствие»).

Большей свободой и математическим осмыслением обладает процедура оцифровки номинальных шкал. В это случае, как правило, не играет роли порядок следования и расстояния между градациями признаков.

 

" Хотя возможны и исключения – для примера возьмем признак «Отрасль промышленности». Значения признака «цветная металлургия» и «черная металлургия» психологически воспринимаются ближе, чем «нефтяная промышленность» и «пищевая промышленность», хотя признак, обозначающий принадлежность предприятия к определенной отрасли нельзя назвать порядковым. Для упорядочивания значений шкалы признака можно пользоваться методами многомерного шкалирования и в конечном счете возможно, что признаку будут отвечать не одна, а несколько числовых меток, если построенное «пространство восприятия» окажется эффективно двумерным. "

 

Свобода в выборе числовых меток для номинальных шкал дает возможность искусственно упростить структуру набора данных, например, добиться того, чтобы шкалы признаков были максимально скоррелированы друг с другом. Популярным методом является максимизация функционала Q, где

,

где r_ij – коэффициент линейной корреляции между i-ым и j-ым признаком, m – число признаков, среди которых есть как номинальные, так и количественные. Допустим, что номинальным признаков уже были каким-то образом присвоены числовые метки. Тогда

,

где в Q₁ входят коэффициенты корреляции между номинальными признаками, подлежащими оцифровке, в Q_1,2 – коэффициенты корреляции между номинальными и количественными признаками, а Q₂ – часть функционала, состоящая из коэффициентов корреляции между количественными признаками. Последняя не зависит от оцифровки и оптимизации на самом деле подлежит функционал , где

Пусть X⁽¹⁾ – набор номинальных признаков, подлежащих оцифровке, X⁽²⁾ – набор количественных признаков, – числовая метка, присвоенная k-ой категории i-го номинального признака. N(i,j) – матрица сопряженности между i-ым и j-ым номинальными признаками, в качестве оценки которой можно взять числа n_kl(i,j) одновременного появления для i-го признака категории k, а для j-го признака – категории l, p_i,k – частота появления k-ой градации признака i, который имеет l_i градаций, P_i=diag(p_i,1;p_i,2..,p_i,li); наконец, – среднее значение количественного признака j (jÎX⁽²⁾) на тех объектах, у которых i-ый номинальный признак имеет категорию k.

Тогда градиент функционала

, где

,    iÎX⁽¹⁾, k=1..l_i .

При этом предполагается, что все данные (включая номинальные признаки) предварительно нормированы на единичную дисперсию и центрированы. Для номинальных признаков это означает, что

,  для всех j, k; N – число объектов; – значение числовой метки для i-го объекта. Выполнения этих условий всегда можно добиться линейным преобразованием.

Зная градиент функционала можно воспользоваться любым из методов градиентной оптимизации. Для количественных шкал значения признаков в результате не меняются, а значения меток номинальных признаков назначаются категориям таким образом, чтобы они были максимально скореллированы друг с другом и с количественными признаками, что приводит к снижению эффективной размерности пространства данных (часть признаков становится статистически линейно зависима от других).

 

2.1.3. Нормировка данных

 

После того, как все признаки оказываются описанными в количественной шкале, их обычно центрируют и нормируют.

Первым шагом в статистической обработке данных, как правило, является нахождение точки среднего значения всех признаков – геометрического центра многомерного облака точек данных. Обычно удобно сдвинуть все точки данных на один и тот же вектор таким образом, чтобы центр облака оказался в начале координат.

Далее следует нормировка – то есть деление всех значений признаков на определенное число таким образом, чтобы значения признаков попадали в сопоставимые по величине интервалы. В качестве такого числа обычно выбирается один из характерных масштабов.

В многомерном облаке данных существует несколько масштабов. Во-первых, это квадратный корень из общей дисперсии облака данных, называемый среднеквадратичным отклонением:

, .

Напомним, что здесь и далее большими буквами X_i обозначаются вектора данных, а маленькими – x_ij: j‑ая координата i-го вектора.

В случае, если выборка может считаться полученной из нормального распределения, то в шаре с центром в  радиусом s находится около двух третей от числа точек данных.

Существует масштаб, характеризующий максимальный разброс в облаке данных

.

Нормировка всех признаков на R приводит к тому, что все облако данных оказывается заключено в шар единичного радиуса.

Если в качестве масштаба выбраны s или R, то соответствующие формулы предобработки (нормировки на «единичную дисперсию» и «на единичный шар») имеют вид:

, ,

где – новые и старые значения векторов признаков.

С помощью масштаба s , как правило, определяются понятия кластера и сгущения в облаке данных. Приведем эти определения (см. [4]).

Кластер – группа точек G такая, что средний квадрат внутригруппового расстояния до центра группы меньше среднего расстояния до общего центра в исходном наборе объектов, т.е. , где ,.

Сгущение –  группа точек G такая, что максимальный квадрат расстояния точек из G до центра группы меньше s ², т.е. , где  ,.

 

" К сожалению, такие определения не всегда соответствуют интуитивным представлениям о кластерах и сгущениях – например, когда сгущение представляет из себя сильно вытянутое облако точек. "

 

Кроме того, если диапазоны значений для разных признаков очень сильно отличаются друг от друга, то разумно для каждого из признаков применять собственный масштаб. Для каждого из признаков можно ввести свое среднеквадратичное отклонение и разброс:

, , ,

где x_ij – значение j-го признака на i-ом объекте. Как результат, получаем формулы для нормировки на «единичную дисперсию для каждого из признаков» и «на единичный куб»:

, .

Эти нормировки не являются «изотропными», то есть они сжимают облако данных в некоторых направлениях сильнее, в некоторых – меньше, что в некоторых случаях является желательным, а в некоторых – нарушает структуру данных (взаимных расстояний). Такая нормировка фактически эквивалентна выбору взвешенной евклидовой метрики, о которой речь пойдет ниже.

Наконец, следует упомянуть, что с каждым из количественных признаков  могут быть связаны еще два масштаба – это точность и допуск (см раздел 1.1), с помощью которых также можно «обезразмерить» значения этих признаков.

 

2.1.4. Выбор метрики для пространства данных

 

Любая нормировка данных приводит к тому, что изменяются взаимные расстояния между точками данных. Это можно истолковать как выбор метрики иной по сравнению с обычной евклидовой. Выбор метрики является важным моментом в любой методике анализа структуры данных.

Сначала введем понятия матрицы связи признаков и матрицы расстояний между объектами.

Матрица связи – квадратная симметрическая матрица размерами m´m типа «признак-признак», где на пересечении i-ой строки j-ого столбца стоит мера «взаимосвязанности» i-го и j-го признака. Самой популярной мерой связи количественных признаков является коэффициент корреляции Пирсона, который вычисляется по формуле

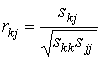, где  .

В результате матрицей связи становится корреляционная матрица

 

.

 

" В случае применения порядковых и номинальных шкал могут применяться другие меры связи такие как коэффициент ранговой корреляции для вычисления связи между порядковыми признаками или бисериальный коэффициент корреляции, применяемый для измерения связи между порядковым и количественным признаком. Подробный анализ этих коэффициентов приведен в [28] "

 

Матрица расстояний – квадратная матрица размерами N´N типа «объект-объект», где на пересечении i-ой строки j-ого столбца стоит мера удаленности между i-ым и j-ым объектом:

 

.

 

Для того, чтобы величины d_ij имели смысл расстояний между объектами в многомерном пространстве, необходимо, чтобы для всех i, j = 1…N выполнялись требования:

1. Максимальное сходство объекта с самим собой: .

2. Требование симметрии: d_ij = d_ji .

3. Выполнение неравенства треугольника: d_ij £ d_ik + d_kj .

 

Если введенная мера удаленности между объектами такова, что выполняется это условия, то будем называть D матрицей расстояний.

 

" Данные могут быть исходно заданы в виде матрицы связи или удаленностей. Тогда возникает задача по заданной матрице восстановить в каком-либо смысле исходное множество точек данных таким образом, чтобы для него матрица связанности или удаленностей имели заданный вид (точно или приближенно). "

 

Правило вычисления расстояния между объектами может сильно видоизменяться в зависимости от специфики задачи. Если такое правило задано, то говорят, что в пространстве признаков введена метрика. Рассмотрим различные правила измерения расстояний:

I. Квадратичные метрики:

Для класса квадратичных метрик квадрат расстояния между объектами  является квадратичной формой от разностей значений их координат:

 

,

где G – симметричная положительно определенная матрица.

 

В качестве матрицы G размерами m´m можно выбрать

а) единичную матрицу G = E, в результате чего получаем обычное евклидово расстояние

;

б) диагональную матрицу G = diag(g₁,g₂…g_m), в результате получим взвешенную евлидову метрику

;

в) матрицу, обратную ковариационной матрице G = S^-1 :

, где ,

что дает махаланобисову метрику.

С ковариационной матрицей связано понятие эллипсоида рассеяния облака точек. Осями эллипсоида рассеяния являются направления собственных векторов S (поскольку S-симметричная матрица, то собственные вектора образуют полную ортогональную систему векторов), длины осей выбираются равными значениям соответствующих собственных чисел.

Особенностью махаланобисовой метрики является то, что в ней эллипсоид рассеяния точек данных является шаром с единичным радиусом.

 

Основным преимуществом использования квадратичных метрик является тот факт, что производная от квадрата расстояния, измеренного в такой метрике является линейной функцией от координат объектов, что может быть использовано при решении различных задач (например, задач оптимизации).

 

II. Специальные виды метрики:

 

а) городская метрика или расстояние Минковского:

,

применяется для измерения расстояний между объектами, описываемыми в порядковой шкале; I_k(X_i,X_j) – разница в номерах градаций по k-ому признаку у сравниваемых объектов c векторами X_i и X_j;

б) Расстояние Хэмминга

чаще всего применяется для измерения расстояния между объектами, описываемыми в дихотомической шкале. Тогда расстояние Хэмминга – число несовпадающих значений признаков в рассматриваемом i-ом и j-ом объектах.

в) расстояние Колмогорова

является обобщением евклидовой метрики. Так, при p = 1 получаем метрику Хэмминга, при p = 2 – евклидову метрику, при p = ¥ – метрику «по максимуму модуля»:

Все эти метрики  допускают тривиальное обобщение, если производить суммирование с весами и тогда получаем взвешенную городскую, взвешенную Хэммингову и взвешенную метрику Колмогорова. Веса признаков подбираются или с помощью простых эвристических методов, или настраиваются с помощью специальных процедур (см., например, [4]).

 

III. Риманова метрика

 

Риманова метрика является обобщением квадратичной метрики в случае точечного пространства. В ней задается квадратичное расстояние между бесконечно близкими точками

,

где ,– бесконечно малые приращения координат, g_ij – метрический тензор. Значения g_ij зависят от точки пространства, в которой измеряется расстояние между бесконечно близкими точками. Тогда расстояние между объектами измеряется с помощью интеграла по траектории и, вообще говоря, зависит от выбора траектории, соединяющей два объекта

.

Если мы предполагаем, что расстояния измеряются по кратчайшему пути, то среди всех траекторий L выбирается та, при использовании которой расстояние оказывается наименьшим

.

Такая траектория называется геодезической и играет роль, аналогичную прямой в евклидовом пространстве.

Приведем несколько простых видов римановых метрик

а) , где f₁(x), f₂(x), f₃(x) – монотонные функции одного аргумента. По существу такая метрика может быть преобразована в евклидову нелинейным преобразованием координат ;

б) конформно-плоская метрика

,

где d_ij – символ Кронеккера.

В общем случае эта метрика не может быть превращена в евклидову сразу во всем пространстве никаким нелинейным преобразованием координат. Ее смысл состоит в том, что масштаб, с помощью которого измеряются расстояния, меняется от точки к точке пространства.

 

2.1.5. Настройка метрики

 

При использовании взвешенных метрик остаются неопределенными веса признаков. Иногда условия задачи позволяют выделить те признаки, которые являются «более значимыми» при измерении расстояний и назначить для этих признаков значения весов. Если никаких дополнительных соображений нет, то для настройки весов могут быть использованы некоторые специальные приемы. Приведем примеры:

 

1) Адаптивные квадратичные метрики:

 

Рассмотрим метрику

,

d_ij – расстояние между i-ым и j-ым объектом.

Положим, что det G = 1. Такой выбор не делает результаты менее общими, но его использование позволяет не рассматривать решения, отличающиеся друг от друга только преобразованием гомотетии (равномерным растяжением по всем осям). Допустим, что на наборе объектов уже существует определенная система отношений – объекты разбиты на k непересекающихся классов. Введем матрицу внутриклассового разброса W:

 

,

 

где T – обозначение операции транспонирования, K_i – обозначение множества объектов, принадлежащих i-ому классу.

Если выбрать G = aW^-1, a – числовой множитель, то минимальной (среди всех квадратичных метрик) оказывается величина внутриклассового разброса

,

где – квадрат расстояния между l-ым и m-ым объектом,

что приводит к тому, что классы оказываются максимально компактными [4].

Если разбиение на классы не заданно изначально, то возможна такая настройка метрики, при которой данные будут разбиты на k кластеров «наиболее контрастно». Итерационный алгоритм состоит из двух фаз:

Фаза 1. При фиксированной метрике G^(t) производится разбиение множества данных на k кластеров тем или иным способом (см, например, [1,30]). Число кластеров задается в начале работы и далее не меняется.

Фаза 2. По полученной классификации строится матрица внутриклассового разброса W и вводится метрика G^(t+1) = (W^(t+1))^-1.

Шаги алгоритма повторяются до тех пор, пока относительные изменения значений элементов G не станут меньше заданного числа e.

При использовании взвешенной евклидовой метрики вычисление весов может быть упрощено. В качестве их значений можно выбрать , где w_kk – k-ый диагональный элемент матрицы W, a – нормирующий множитель (например, при получаем равенство det G^(t) = 1 ).

 

2) Использование частично-обучающих выборок

 

Частично обучающая выборка (ЧОВ) – множество пар объектов, относительно которых известно, что они принадлежат одному классу [4]. Естественно считать такие объекты близкими.

Введем аналог матрицы внутриклассового разброса для ЧОВ:

 

, (X_1i, X_2i – i-ая пара из ЧОВ).

 

Если W невырождена, то оптимальную метрику получим, выбирая , где a – нормирующий множитель.

Задачу можно упростить, используя взвешенную евклидову метрику и выбирая

 

, .

 

3) Максимизация корреляций.

 

Рассмотрим риманову метрику. Можно попытаться подобрать вид функций f_i(x) таким образом, чтобы признаки оказались максимально скоррелированы. В качестве критерия, по которому ищется преобразование, можно использовать величину

, r_ij – коэффициент корреляции между i-ым и j-ым признаком.

Функции могут быть выбраны из некоторого семейства монотонных преобразований, например, преобразования Бокса-Кокса [4]:

 

 

или более общее двухпараметрическое семейство

 

.

 

Тогда и критерий Q  может быть максимизирован по параметрам a_k, b_k, k=1…m.

 

4) Контрастирование структуры данных

 

Рассмотрим такой вариант римановой метрики, в котором плотность данных оказалась бы почти равномерной или, наоборот, структура сгущений оказалась бы более контрастной.

Элемент объема риманова пространства вычисляется по формуле , где  – определитель матрицы метрического тензора.

Оценим нормированную на одну точку плотность распределения данных в исходном пространстве с помощью какой-либо непараметрической оценки. Например, пусть

 

,

 

где K(x) – некоторая функция, удовлетворяющая условию , например , s - радиус «области влияния», который является свободным параметром или может быть оценен методами непараметрической статистики.

Допустим, в новом пространстве плотность распределения будет постоянна:. Например, можно выбрать , где V – исходный объем фазового пространства данных (который, очевидно, конечен).

Положим, что метрика пространства имеет конформно-плоский вид:

 

,

где - конформный множитель, зависящий от точки x. Для того, чтобы плотность данных в новом пространстве стала постоянной (может быть за исключением граничных областей), необходимо выбрать

.

С другой стороны, выбирая

, a > 0

получаем метрику, в которой сгущения данных выглядят тем более контрастно, чем больше параметр a. Малые расстояния между точками данных в такой метрике становятся еще меньше, большие – больше.

 

2.1.6. Вычисление расстояний для данных с пробелами

 

Отдельные значения координат точек данных могут оказаться либо недостоверными, либо вообще неизвестными, и тогда объект в многомерном пространстве надо представлять не точкой, а прямой или гиперплоскостью, параллельной координатным осям. Как измерять расстояния между объектами в таком случае?

Будем вычислять такие расстояния как расстояния между соответствующими геометрическими образами (между точкой и прямой, точкой и плоскостью, прямой и прямой и т.д.) В результате получим очень простое правило вычисления расстояний между объектами с пропущенными значениями признаков – расстояния вычисляются в том подпространстве, в котором значения координат у объектов известны полностью. Иными словами, при подсчете сумм в формулах вычисления расстояний те слагаемые, которые не могут быть вычислены из-за того, что отдельные значения признаков неизвестны, просто пропускаются.

Покажем, что это так. Допустим, объект имеет следующие значения признаков

.

Значком @ мы обозначили неизвестное значение признака x_k. Пусть X(k) обозначает, что у объекта X неизвестно значение  k-ого признака, а X⁰(k) обозначает следующий набор признаков:

,

то есть k-ое значение признака заменено нулем.

Тогда геометрический образ, который можно сопоставить объекту X(k) – прямая

, где e_k  – единичный орт k-ой координатной оси.

Пусть значения признаков объекта Y известны полностью. Тогда найдем кратчайшее расстояние между   и :

      .

Это означает, что при вычислении расстояния неизвестное значение k-го признака у X необходимо заменить значением k-го признака Y. Но тогда

,

то есть при вычислении расстояний можно просто приравнять к нулю значение k-го признака объектов X и Y. Тогда, например, в случае евклидова расстояния получаем формулу для вычисления расстояния

.

Рассмотрим, что будет, если у объекта Y неизвестно значение l-ого признака. Тогда

,

.

Если , то  ,  и приходим к той же ситуации, что и в случае с точкой и прямой. Если , то  и  и вновь мы просто пропускаем неизвестное значение признака.

Совершенно аналогично обстоит дело в общем случае, когда и X, и Y содержат произвольное число пропущенных признаков.

Теперь вернемся к случаю, когда у Y известны все значения признаков, а для X неизвестно значение k-го признака, но известно, что оно лежит в диапазоне [a_k,b_k] (объект представляется отрезком прямой). Тогда правило вычисления расстояния между X и Y окажется следующим: если , то как и прежде пропускаем значение признака, иначе, если , то полагаем , а если , то  и считаем расстояние.

 

2.1.6. Гравитирующие данные

 

Процедуры предобработки данных могут заключаться не только в нормировке данных и выборе метрики, но и в целенаправленном изменении расстояний между точками для подчеркивания определенных особенностей структуры облака точек.

Рассмотрим предложенный в главе I вариант преобразования данных как облака гравитирующих точек. Припишем каждой точке X_i  «массу» m_i. «Типичные представители» классов, например, могут иметь большую массу по сравнению с другими. В самом простом случае все массы равны.

Будем использовать евклидову метрику для измерения расстояний между точками, тогда

Введем потенциал взаимодействия между точками X_i и X_j. Рассмотрим простой случай центральных сил и предположим, что потенциал не зависит от номеров точек i и j:

,

j (r) – потенциальная функция, зависящая только от расстояния между точками. Тогда энергия взаимодействия пары точек

и суммарная энергия

.

Тогда

.

Будем считать, что легкая частица движется в вязкой среде, так что инерция движения гасится средой. Тогда уравнение движения оказывается первого порядка:

.

Проще всего решать это уравнение по схеме Эйлера, что дает следующую итерационную формулу:

.

Шаг Dt должен быть достаточно мал, чтобы обеспечить адекватность решения.

Теперь вспомним, что наша Вселенная данных должна раздуваться, чтобы обеспечить постоянную плотность данных. Этого эффекта можно достигнуть простой перенормировкой данных на первоначальный объем. Для этого нужно вычислить новый фазовый объем данных V^(t+1) – объем прямоугольного параллелепипеда со сторонами, равными диапазонам значений признаков. Тогда получаем окончательный итерационный алгоритм:

Шаг 1. Движение частиц

Шаг 2. Перенормировка.

На этом шаге можно предложить два варианта:

1) изотропный (расширение происходит одинаково во всех направлениях):

, где V⁽⁰⁾ – начальный объем данных.

В этом варианте возможно «схлапывание» Вселенной данных вдоль какого-то направления (параллелепипед может начать неограниченно вытягиваться).

2) неизотропный (расширение происходит так, чтобы сохранять форму исходного фазового объема)

,

где – диапазон изменения значений k-го признака на шаге t.

 

Теперь рассмотрим некоторые варианты потенциальных функции j(r):

1) ньютоновский потенциал без сингулярности

Если a < 0, то данные притягиваются и их кластерная структура становится более контрастной, при a > 0 – отталкиваются и распределение становится более равномерным (но отношения соседства при этом нарушаются не слишком сильно) . Регуляризующая постоянная e² нужна для того, чтобы точки данных не испытывали слишком сильных перемещений (за времена порядка Dt) вблизи r = 0.

2) потенциал ядерных сил

.

Смысл постоянной r₀ – эффективный радиус взаимодействия: на расстояниях больше r₀ точки данных практически «не замечают» друг друга.

3) использование других степенных зависимостей

.

Так, для многомерного ньютоновского потенциала  .

 

2.1.8. Локальные статистики

 

Рассмотрим вкратце идею локальных статистик, которая тоже может быть использована при обработке данных перед применением процедур визуализации.

Выберем k-ый объект, который будет играть роль базового. Перейдем к новой векторной переменной r’ = r – r_k , или, что тоже самое – отцентрируем данные так, чтобы k-ый объект оказался в начале координат:

, p = 1…N.

Теперь введем квадратичную метрику

,

G_k – положительно определенная симметричная матрица. Ее коэффициенты могут быть настроены из различных соображений. Приведем два самых простых:

1) Оптимизация разделения классов. Коэффициенты настраиваются из условия минимума функционала

, где w_k  – класс, к которому изначально принадлежал объект X_k.

Таким образом, объекты того же класса, что и X_k, оказываются в результате ближе к началу координат (где находится X_k), чем все остальные объекты.

2) Нормализация распределения

Матрица , где

.

Если матрица W_k невырождена, то G_k существует и в результате распределение векторов  «с точки зрения» будет выглядеть похожим на нормальное.

Для решения упомянутых задач можно упростить G_k, выбрав ее диагональной (метрика окажется взвешенной евклидовой):

, .

Тогда, например, для нормализации распределения можно выбрать , где – i-ый диагональный элемент W_k.

Построенное пространство признаков можно анализировать (и визуализировать) любыми методами анализа многомерных данных. В результате мы получим описание набора данных «с точки зрения» объекта X_k. Строя N таких пространств (и получая N описаний) и сравнивая их между собой, можно сделать полезные выводы об структуре данных. Разумеется, для эффективного сравнения N результатов обработки необходимо каким-то образом автоматизировать этот процесс, выдавая уже «сухой остаток» результатов сравнения.

Другой способ состоит в конструировании нового пространства, которое определенным образом «обобщает» все построенные пространства. Допустим, построены N метрик , k = 1…N. Тогда можно записать такую матрицу удаленностей:

 

,

 

где на пересечении i-ой строки и j-го столбца стоит расстояние между i-ым и j-ым объектом в метрике, построенной для i-го объекта. Поскольку для различных объектов будут построены различные метрики, то для элементов матрицы D могут не выполняться условия симметричности () и неравенства треугольника (может быть больше ). Поэтому такая матрица не может напрямую служить матрицей расстояний.

Попробуем устранить указанные нарушения, вводя новый класс так называемых d^(s)-метрик:

, k = 1…N,

где d_ik, d_jk – элементы i-ой и j-ой строк матрицы D; j(x) – монотонная функция, например,  j(x) = x или j(x) = rank(x) – преобразование к порядковой шкале; s[…,…] – мера подобия двух последовательностей; a, b – константы, значения которых подбираются с целью масштабирования и выполнения метрической аксиомы неравенства треугольника. Тогда расстояние между объектами в d^(s) метрике имеет ясный смысл – это различие двух последовательностей чисел – всех расстояний до объекта X_i в метрике d_i и всех расстояний до объекта X_j в метрике d_j.  Другими словами – это мера сходства двух представлений данных – с точки зрения объекта X_i и X_j.

В качестве конкретных вариантов d^(s)-метрик могут быть использованы:

 

d^(d)-метрика:

основана на простой евклидовой формуле для сравнения последовательностей. Она автоматически обеспечивает выполнение условия симметричности и неравенства треугольника, однако нивелирует некоторые важные особенности рядов j(d_ik) и j(d_jk).

 

d^(s)-метрика, основанная на стандартных мерах связи:

,

где в качестве s_ij, можно выбрать коэффициент корреляции Пирсона (что обеспечивает условие симметрии, но возможны незначительные нарушения неравенства треугольника) или коэффициент связи t-Кендалла между ранговыми признаками (обеспечивает выполнение всех условий).

 

После того, как исследователь остановится на том или ином варианте d^(s) метрики, матрица D преобразуется таким образом, чтобы она могла служить матрицей расстояний для некоторого распределения точек данных. После этого можно применять те методы анализа данных, в которых исходной информацией служит матрица расстояний (например, методы метрического шкалирования).

 

 

2.2. Линейный анализ данных

 

Теперь перейдем к краткому описанию традиционных линейных методов анализа, которые так или иначе можно использовать для визуализации структуры данных.

Сначала выпишем формулы, которыми описывается случайная величина (вектор), подчиненная многомерному нормальному закону распределения. Плотность вероятности в этом случае равна

, .

Здесь MX – математическое ожидание X, S – ковариационная матрица

 

 .

 

Величина MX и ковариационная матрица оцениваются с помощью данных выборки:

, .

 

2.2.1. Метод главных компонент

 

Как уже упоминалось, цель анализа данных – извлечение содержащихся в них информации. Задача снижения размерности набора данных – описание каждой точки данных с помощью величин, число которых меньше размерности пространства и которые являются функциями исходных координат

 

, k = 1…m’ , m’ < m.

 

Функции F_k задают отображение F из исходного пространства R^m в пространство R^m’. Это отображение должно выбираться таким образом, чтобы на наборе данных X максимизировать определенный критерий, как-то отражающий количество сохраняемой при этом преобразовании информации. Выбирая отображение F из определенного класса отображений и критерий сохранения информации J, можно получать различные методы сокращения размерности пространства признаков.

В методе главных компонент F – некоторое линейное ортогональное нормированное отображение, т.е.

, где – средние по набору данных значения признаков, а на коэффициенты c_ij накладываются условия

, , i, j = 1…m, i ¹ j.

Вид критерия J :

,

где D – вычисление дисперсии случайной величины.

Согласно этому критерию, количество сохраненной информации равно доле «объясненной» с помощью новых признаков h₁…h_m дисперсии исходных признаков.

Первой главной компонентой называют такую нормированно-центрированную линейную комбинацию исходных признаков, которая среди всех прочих нормированно-центрированных линейных комбинаций обладает на данном наборе данных наибольшей дисперсией.

Решим задачу нахождения первой главной компоненты. Для этого необходимо решить задачу

 

,

где – вектор-строка размерности m, при условии нормировки . Вектор можно представлять как единичный вектор пространства данных, тогда  – точка проекции вектора на вектор .

Положим, что система векторов данных является центрированной, т.е.  Тогда

,

где S – ковариационная матрица набора данных X.

Введем функцию Лангранжа , тогда

,

и

,

то есть – собственный вектор ковариационной матрицы. Но , значит для того, чтобы достигало максимума, нужно выбрать максимальное собственное значение. Нормированный собственный вектор, отвечающий этому значению и задаст направление первой главной компоненты в пространстве.

k-oй главной компонентой (k = 2…m) называется такая нормированно-центрированная линейная комбинация исходных признаков, которая не коррелирована с k-1 предыдущими главными компонентами и среди всех прочих нормированно-центрированных линейных комбинаций, не коррелированных с предыдущими k-1 главными компонентами обладает на данном наборе данных наибольшей дисперсией.

Можно показать, что k-ая главная компонента задается собственным вектором ковариационной матрицы данных, который соответствует k-ому по величине собственному значению.

Заметим, что решение задачи нахождения главных компонент не является инвариантным относительно смены масштабов у разных признаков. Поэтому перед применением метода данные нормируются так, чтобы все признаки были измерены в сопоставимых масштабах.

 

На m’ главных компонент можно натянуть подпространство размерности m’. Легко понять, что сумма квадратов расстояний от точек данных до этого подпространства  равна умноженной на N (число точек) остаточной дисперсии, «не объясненной» с помощью m’ главных компонент, то есть , где ,…, – наименьшие по величине собственные значения. Отсюда становится понятным важное экстремальное свойство указанного подпространства:

Свойство 1. Сумма квадратов расстояний от исходных точек-наблюдений ,…, до пространства, натянутого на m’ главных компонент наименьшая среди всех других подпространств размерности m’, полученных с помощью произвольной линейно-независимой системы из m’ векторов.

Укажем еще два экстремальных свойства подпространства главных компонент.

Зададим правило перехода к меньшему числу переменных с помощью линейного преобразования:

, j = 1…m’, i = 1…N, или

Z = CX,

здесь – k-ая координата вектора данных X_i, z_ij – j-ая координата i-ой точки данных в некотором подпространстве меньшей размерности R^m’. Можно рассматривать эти формулы как проекцию точек данных из исходного пространства в R^m’.

Рассмотрим величины

,

.

Их смысл – сумма квадратов расстояний между всевозможными парами объектов в исходном пространстве и в R^m’. Введем в качестве меры искажения суммы квадратов попарных расстояний между точками данных величину M-M(C). Можно показать [4], что

,

где L – матрица, задающая проекцию точек данных в подпространство, натянутое на m’ главных компонент. Отсюда сдедует

Свойство 2. Среди всех подпространств размерности m’ , полученных из исходного пространства данных с помощью произвольного линейного преобразования исходных координат, в подпространстве, натянутом на первые m’ главных компонент наименее искажается сумма квадратов расстояний между всевозможными парами рассматриваемых точек.

Наконец, введем меру искажения расстояний до начала координат и углов между прямыми, соединяющими всевозможные пары точек с началом координат. Обозначим ее , где

,

,

а под – евклидова норма матрицы A. Оказывается, что

.

То есть справедливо

Свойство 3. Среди всех подпространств размерности m’ , полученных из исходного пространства данных с помощью произвольного линейного преобразования исходных координат, в подпространстве, натянутом на первые m’ главных компонент наименее искажаются расстояния от точек до начала координат, а также углы между прямыми, соединяющими всевозможные пары точек с началом координат.

Наконец, отметим, что указанное вначале требование «центрированности» данных не является принципиальным. Если в данных нет пробелов, то геометрический центр облака точек определен однозначно. Отличия в формулировках свойств 1-3 будет лишь в том, что вместо линейного подпространства, натянутого на главные компоненты надо рассматривать линейное многообразие, построенное на первых главных компонентах и проходящее через точку геометрического центра.

 

2.2.2. Итерационный алгоритм нахождения главных компонент

 

Используя экстремальное Свойство 1 подпространств, натянутых на главные компоненты, можно предложить итерационный алгоритм нахождения первой главной компоненты (ср. с [41,53]). Будем искать прямую в пространстве данных, заданную параметрическим уравнением

,

такую, что сумма квадратов расстояний от точек данных до этой прямой минимальна. Эта сумма, равная

является критерием, который можно минимизировать с помощью следующей простой процедуры:

Зададимся произвольными векторами a и b. Далее итерация алгоритма состоит из двух шагов:

Шаг 1. При заданных векторах a и b определяется набор {t_i}, i = 1…N:

,

.

Шаг 2. При заданном наборе {t_i} определяются новые координаты векторов a и b:

,

,

что дает m систем линейных уравнений 2x2 для определения всех компонент векторов a и b.

Проверка на останов. Алгоритм останавливается, когда , где  – изменение величины  за итерацию, а  – малая величина.

 

Преимущество такого способа нахождения первой главной компоненты состоит в том, что он легко обобщается на случай, когда некоторые данные содержат неполные значения. Рецепт прост – если в соответствующей сумме встречается неизвестное значение, то такое слагаемое пропускается. Тогда, если неполных данных нет, то b дает вектор среднего значения всех координат: , иначе – некоторый «эффективный» вектор среднего. Вектор a в случае полных данных задает направление первой главной компоненты, в случае неполных – «эффективную» первую главную компоненту.

Для того, чтобы найти вторую главную компоненту, поступают следующим образом:

1. Рассчитывается множество векторов первых остатков : . Это множество лежит в пространстве, ортогональном первой главной компоненте, размерностью на единицу меньше размерности исходного пространства данных.

2. Для нового множества векторов рассчитывается первая главная компонента. Она и будет второй главной компонентой исходного набора данных.

Для нахождения третьей главной компоненты ищется множество вторых остатков и для него определяется первая главная компонента, и т.д.

 

2.2.3. Модели линейного факторного анализа

 

Напомним, что метод главных компонент может быть сформулирован как задача оптимизации функционала J качества «сохранения» информации при заданном отображении F из исходного пространства в пространство меньшей размерности. В методе главных компонент в качестве функционала J выступает доля «объясненной» с помощью новых координат дисперсии.

В модели факторного анализа каждому вектору данных X_i сопоставляется набор из m’ значений факторов ,…,:

, j = 1…m’, или

,

где – среднее значение j-го признака, – значение j-го признака для i-го объекта, q_ij – «нагрузки» факторов, u^j – остаточная случайная компонента. При этом выполняются условия:

, , ,

и ,…,, ,…,попарно некоррелированы.

В качестве F выбирается линейное преобразование координат такое, чтобы выполнялись эти условия, и достигал максимума функционал

,

где  – корреляционная матрица исходных признаков,  – корреляционная матрица «проекций» в пространство факторов ,  – евклидова норма матрицы A.

Поясним выкладки. Матрица нагрузок Q размерами m’´m осуществляет линейное отображение из пространства факторов (размерности m’) в исходное пространство (размерности m). В результате получается множество данных , которое совпадает со множеством исходных данных с точностью до случайной компоненты U. Это множество лежит в некотором подпространстве размерности m’, натянутом на m’ столбцов матрицы Q. Матрица Q и исходный набор факторов ,…,, i = 1…N выбираются таким образом, чтобы корреляционная матрица набора данных максимально точно воспроизводила корреляционную матрицу исходного набора данных. Таким образом, критерием количества «сохраненной» информации является здесь объяснение не дисперсии признаков, а их взаимной скоррелированности.

Что касается «шумовой» компоненты U, то обычно полагают, что она не зависит от распределения данных и подчинена m-мерному нормальному распределению с нулевым средним значением. Тогда ковариационная матрица распределения U имеет диагональный вид:

, , .

Если исходное распределение данных предполагается центрированным, то его ковариационная матрица

Решением задачи факторного анализа называют пару матриц (Q,V), удовлетворяющую этому условию. Очевидно, что если одно такое решение существует, то одновременно решением является (QC,V), где C – произвольное ортогональное преобразование (поворот векторов-столбцов матрицы Q). По этой и другим причинам решение задачи факторного анализа является неоднозначным, поэтому для ее решения необходимо выбрать какие-либо дополнительные предположения о свойствах матрицы Q. Независимо от этих предположений итерационный метод решения задачи выглядит следующим образом.

 

Вначале задается нулевое приближение матрицы V=V⁽⁰⁾.

Шаг 1. Получаем нулевое приближение матрицы Y = QQ^T, т.е. Y⁽⁰⁾ = S – V⁽⁰⁾.

Шаг 2. С помощью Y⁽⁰⁾ определяем нулевое приближение матрицы Q.

Алгоритм продолжается до получения необходимой точности.

 

Дополнительные предположения о структуре матрицы Q используются для реализации Шага 2 алгоритма. Рассмотрим два условия:

1) Q^TQ – диагональная матрица, причем диагональные элементы различны и упорядочены в порядке убывания.

Тогда

, ,

,

то есть m’ столбцов q₁…q_m’ матрицы Q удовлетворяют уравнениям  на собственные значения матрицы Y. Собственные вектора матрицы Y, отвечающие первым m’ по величине собственным значениям и составят очередное приближение матрицы нагрузок Q.

2) Q^TVQ – диагональная матрица, причем диагональные элементы различны и упорядочены в порядке убывания.

Тогда

, ,

,

то есть m’ столбцов q₁…q_m’ матрицы Q удовлетворяют уравнениям  на обобщенные собственные значения матрицы Y. Обобщенные собственные вектора матрицы Y, отвечающие первым m’ по величине обобщенным собственным значениям составляют очередное приближение матрицы нагрузок Q.

 

Подведем некоторые итоги. По данному набору данных, используя метод главных компонент или методы факторного анализа, можно построить линейные модели данных. Фактически эти методы строят специальное линейное многообразие меньшей размерности, на которое проецируются исходные данные. Это подпространство оказывается в некотором смысле оптимальным среди всех других линейных многообразий той же размерности. В случае метода главных компонент оптимальность заключается в том, что проекции данных максимально воспроизводят дисперсию исходных данных. В случае методов факторного анализа значения признаков проекций максимально похожи на исходные значения признаков в смысле взаимной корреляции. Следует заметить, что в случае, когда остаточные дисперсии (суммарные расстояния до построенного подпространства) невелики, оба метода дают сходные результаты (это становится особенно понятно, если рассмотреть условие 1 на структуру матрицы Q).