Глава 1. Море информации и океан данных
1.1. Возникновение и представление данных
1.1.1. Таблицы данных.
Любое практическое
исследование на начальном этапе включает в себя стадию собирания данных. Если исследователь разрабатывает совершенно
необжитую область, то он склонен понимать под данными практически все, что ему
удается зафиксировать более-менее содержательного и более-менее объективного в
исследуемой системе (разумеется, содержательного и объективного с точки зрения
его самой общей методологии).
Тем не менее, даже если
первопроходец бережно коллекционирует все, что попадается под руку, он вынужден
каким-либо образом систематизировать собранное. Наиболее распространен
следующий подход.
Как правило, исследователь
выделяет в системе объекты, сходные по природе и по своему усмотрению наделяет
всю совокупность таких объектов набором свойств, с помощью которых он
намеревается отличать одни объекты от других той же природы. В обозначении
такого набора свойств или признаков
объекта состоит первый шаг к тому, чтобы придать исследованию определенное
направление, и после такого выбора исследователь уже способен отвечать на один
существенный для поиска вопрос – одинаковы
ли два встреченных явления или они как-то отличаются друг от друга?
В наши задачи ни в коей мере не входит оспаривать универсальность
такого метода – более того, с другими мы работать и не будем. Главное – это то,
что в результате возникает средство для
представления и хранения собранных данных – таблица
данных. В дальнейшем мы будем считать понятия данных и таблицы синонимами, считая,
что все собранные материалы исследователь хранит в виде таблиц.
" Разумеется, таблица данных
может содержать данные не об исследуемых отдельных объектах или явлениях, а
данные о состоянии одного и того же объекта, но в разных ситуациях или в разные
моменты времени. Тогда следует говорить о различии в состоянии одного и того же
объекта. "
Будем представлять, согласно традициям и соображениям удобства, что
каждой строке таблицы соответствует определенный объект или явление изучаемой
системы, а в столбцах таблицы размещаются значения или метки признаков. В
результате получается таблица типа «объект-признак»:
|
|
Признак 1 |
Признак 2 |
Признак 3 |
Признак 4 |
… |
Признак m-1 |
Признак m |
|
Объект 1 |
|
|
|
|
… |
|
|
|
Объект 2 |
|
|
|
|
… |
|
|
|
Объект 3 |
|
|
|
|
|
|
|
|
… |
… |
… |
… |
… |
… |
… |
… |
|
Объект N |
|
|
|
|
... |
|
|
"
Мы намеренно оставляем
в стороне вопрос о том, насколько общо такое представление данных. Однако приведем
пример, где отношения между понятиями объекта и признака объекта несколько
запутываются. Простейшим примером является таблица результатов соревнований,
проведенных по олимпийской системе «каждый играет с каждым». Или пример таблиц,
встречающихся при учете миграционных потоков населения. В строках такой таблицы
стоят страны, а в столбцах – те же страны, но играющие роль центров иммиграции.
На пересечении соответствующей строки и столбца – число иммигрантов.
Одним из способов все-таки представить такие таблицы
в виде «объект-признак» состоит в том, чтобы считать объектом не отдельную
страну, а явление миграции из страны A в страну B. Один
из признаков такого явления – количество иммигрантов и т.п. Таблица в этом случае
«вытянется» по вертикали и предстанет в не совсем привычном виде. "
Характерные примеры
Приведем несколько примеров и
постараемся сделать небольшой обзор способов представить имеющиеся данные в
виде таблиц.
I Пример
1. Экономическая таблица.
В журнале «Эксперт» ежегодно публикуются таблицы экономических
показателей для двухсот самых крупных предприятий России. В числе таких
показателей указываются валовый годовой доход, выраженный в рублях и долларах
по среднегодовому курсу, темп роста предприятия, его балансовая прибыль до и
после налогообложения, а также число работающих и некоторые производные
характеристики, общепринятые в экономике, типа производительности предприятия.
Кроме этого, указана территориальная и отраслевая принадлежность предприятия.
Начальный фрагмент таблицы приведен на рис.1.
|
1999
г. |
1998
г. |
Компания |
Регион |
Отрасль |
Объем
реализации в 1998 г. (млн руб.)** |
Темп роста (%) |
Объем реализации в 1998 г. (млн долл.)*** |
Балансовая прибыль за 1998 г. (млн руб.) |
Прибыль после налогообложения за 1998 г. (млн руб.) |
Количество работающих за 1998 г. (тыс. чел.) |
Производительность труда (тыс. руб./чел.) |
|
1 |
1 |
РАО «ЕЭС России»* |
|
Электроэнергетика |
218802.1 |
2.0 |
22349.5 |
21534.3 |
16045.6 |
697.8 |
313.6 |
|
2 |
2 |
ОАО «Газпром»* |
|
нефтяная и нефтегазовая промышленность |
171295.0 |
23.4 |
17496.9 |
-22147.0 |
-30119.0 |
278.4 |
615.3 |
|
3 |
3 |
Нефтяная компания «ЛУКойл»* |
|
нефтяная и нефтегазовая промышленность |
81660.0 |
52.2 |
8341.2 |
2032.0 |
573.0 |
102.0 |
800.6 |
|
4 |
|
Башкирская топливная компания* |
Башкирия |
нефтяная и нефтегазовая промышленность |
33081.8 |
–9.1 |
3379.1 |
1228.3 |
517.2 |
104.8 |
315.7 |
|
5 |
4 |
Сибирско-Дальневосточная нефтяная компания
(«Сиданко»)****** |
|
нефтяная и нефтегазовая промышленность |
31361.8 |
0.9 |
3203.5 |
|
|
80.0 |
392.0 |
Рис. 1. Таблица экономических показателей крупнейших предприятий России.
В дальнейшем мы познакомимся
с этой таблицей поближе, а сейчас следует отметить некоторые характерные
особенности данных, представленных в этой таблице:
q
большая часть признаков таблицы измеряется числом –
значением соответствующего показателя; все количественные признаки могут принимать любые вещественные значения в
определенном диапазоне; мы можем сравнить два предприятия по значению того или
иного признака (например, отметить, что темп роста ГазПрома больше, чем ЕЭС);
q
данные неполны
– значения некоторых признаков неизвестны или недостоверны по тем или иным
причинам;
q
один из признаков (валовый объем производства) для
разных предприятий принимает значения, отличающиеся на порядки.
q
некоторые признаки (например, принадлежность к
отрасли) не являются числовыми по смыслу (их значения являются лишь метками);
I Пример
2. Медицинская таблица
В Красноярске и не только в нем весьма популярной для апробации
различных методов анализа данных является так называемая таблица осложнений
инфаркта миокарда. Более подробно о ней будет сказано в третьей главе.
Некоторые исследователи, пробовавшие свои силы на этой таблице, утверждают, что
она содержит большинство характерных трудностей и подводных камней, которые
встречаются при анализе таблиц реальных (не модельных) данных. Число признаков
в полном варианте таблицы – 128, поэтому приведем на рис. 2 несколько строк
таблицы с теми признаками, что вошли на экран компьютера.

Рис. 2. Таблица осложнений инфаркта миокарда.
Как и в предыдущем случае отметим характерные черты такого набора
данных.
q
большая часть признаков – это бинарно закодированные
ответы на вопросы, то есть единица
соответствует ответу «да», ноль – «нет»; кроме этого, встречаются такие признаки,
которые хоть и принимают целочисленные значения из определенного диапазона, но
не имеет большого смысла сравнивать двух пациентов по величине таких признаков,
то есть само числовое значение – это тоже всего лишь метка ответа на вопрос
(когда ответов «да» и «нет» - недостаточно).
I Пример
3. Данные мониторинга
Исследователь может по сути
иметь дело с одним и тем же объектом, наблюдая его различные состояния. Весьма
популярным объектом наблюдения является биржа ценных бумаг. Его состояние может
быть охарактеризовано несколькими десятками различных параметров – финансовых
индикаторов, которые изменяются ежедневно или даже ежеминутно.
На рис. 3 изображена
таблица, где показано несколько состояний фондового рынка США, каждое из
которых характеризуется значением и последним изменением шести основных
финансовых индикаторов. Более подробная таблица включает значения нескольких
сотен индексов.
|
Date |
Time |
Dow 30 Industrials |
S&P 500 |
Nasdaq Composite |
AMEX Composite |
Nyse Composite |
|||||
|
Value |
Change |
Value |
Change |
Value |
Change |
Value |
Change |
Value |
Change |
||
|
21.07.2000 |
6.50PM |
10733.56 |
-110.31 |
1480.19 |
-15.38 |
4094.45
|
-90.11 |
927.64
|
-12.14
|
655.38
|
-4.81
|
|
22.07.2000 |
6.50PM |
10628.51 |
-105.05 |
1470.16 |
-10.03 |
4014.14
|
-80.31 |
917.58
|
-10.06
|
650.35
|
-5.03
|
|
23.07.2000 |
6.50PM |
10514.29 |
-114.22 |
1465.01 |
-5.15 |
4004.02 |
-10.12 |
918.62 |
+1.04 |
648.15 |
-2.20 |
Рис. 3. Таблица основных
фондовых индексов США.
I Пример
4. Частотный анализ текстовой базы
данных
В случае, если предметом
исследования является некоторая совокупность текстов (например, все статьи, опубликованные
в журнале за десять лет), то содержание (естественно, не смысловое, а
формальное) этих текстов можно представить в виде частотной таблицы.
Для составления такой
таблицы сначала проводится полный частотный анализ всей текстовой базы и
находятся наиболее часто употребляемые слова (как правило, при частотном
анализе игнорируют различные варианты написания слов, то есть их окончания и
т.д., а также выбрасывают заведомо бессодержательные, но часто употребляемые
слова-связки). В результате составляется словарь из некоторого фиксированного
набора наиболее часто употребляемых слов во всей совокупности текстов. Этот
словарь и играет роль набора признаков, характеризующих каждый отдельный текст
из базы. Каждый признак – это отдельное слово из словаря, его значение для
конкретного текста – число, описывающее сколько раз данное слово было встречено
в тексте.
На рис.4 приводится простая
частотная таблица, где в качестве объектов выбраны разделы этой книги, которые
описываются частотами некоторых самых распространенных в тексте книги слов.
В качестве характерной
особенности данной таблицы укажем следующее:
q
если текстовая база очень неоднородна по содержанию
(например, база из всех статей UseNet), то для того, чтобы можно
было охватить все темы, частотный словарь должен содержать достаточно много
словоформ; необходимое число столбцов в частотной таблице может вырасти до
тысячи; при этом сама частотная таблица окажется очень разреженной – будет
содержать большое количество нулей.
|
Текст |
данн |
точк |
карт |
модел |
сетк |
табл |
визуал |
|
Миркес Е.М. Нейрокомпьютер. Проект
стандарта. |
0.006558 |
0.000822 |
0.000249 |
0.000000 |
0.014876 |
0.003212 |
0.000000 |
|
Горбань А.Н. Демон Дарвина |
0.001367 |
0.000481 |
0.000751 |
0.009319 |
0.000154 |
0.000058 |
0.000019 |
|
Визуализация данных. Глава 1 |
0.025356 |
0.003356 |
0.010938 |
0.007644 |
0.003356 |
0.004164 |
0.001678 |
|
Визуализация данных. Глава 2 |
0.017673 |
0.004564 |
0.004467 |
0.004273 |
0.011750 |
0.000777 |
0.001457 |
|
Визуализация данных. Глава 3 |
0.020914 |
0.000775 |
0.018203 |
0.000387 |
0.003098 |
0.009295 |
0.003486 |
Рис. 4. Частотный анализ
содержания глав этой книги
на фоне двух других книг.
Предложенный способ составления частотных таблиц достаточно широко применяется
для автоматизированного составления каталога текстовых баз. Познакомиться с применениями
такого подхода можно в Интернете (http://websom.hut.fi) и в работах
[7,22,45,77].
I Пример
5. Прогнозирование поведения временного
ряда
Предположим, что результатом некоторых
наблюдений является временной ряд – информация о состоянии какого-то явления
(например, курса доллара на торгах ММВБ) в разные моменты времени. Можно
поставить задачу прогнозирования поведения временного ряда, то есть
предсказания значения каких-то величин в будущие моменты времени. В этом
направлении существуют два подхода.
В первом предполагается, что
значение величины зависит главным образом от некоторых сторонних факторов и
задача предсказания в этом случае сводится к выявлению зависимости
прогнозируемой величины от других факторов. Для такого подхода удобно
представлять временной ряд в естественном виде, то есть выбирать в качестве
признаков время наблюдения, численное значение прогнозируемой величины,
значения остальных факторов, предположительно имеющих отношение к делу.
Второй подход предполагает,
что значение какой-либо величины можно предсказать, если знать ее поведение в
прошлом. В этом случае изучаемый объект – это факт того, что прогнозируемая
величина приняла определенное значение вместе с определенной предысторией
изменения величины в прошлом.
Рассмотрим в качестве
конкретного примера, как можно преобразовать простую таблицу изменения курса
доллара для применения последнего из упомянутых подходов. В качестве признаков выберем
значение самого курса, а также значения курса за последние n дней.
Фрагмент такой таблицы приведен на рис. 5.
q
таблица имеет характерный вид: значения признаков
смещаются в каждой последующей строке на одну позицию вправо.

Рис. 5. Таблица изменений
курса доллара.
Зоология шкал признаков
В вышеописанных примерах объекты исследования
описывались признаками, которые отличались друг от друга допустимыми наборами значений.
Опишем различные типы шкал признаков
согласно общепринятым определениям:
q
непрерывная шкала – признак в этой
шкале может принимать любое вещественное значение; разумеется, некоторые
признаки могут принимать, например, только положительные значения, то есть
лежать в определенном допустимом диапазоне;
q
дискретные шкалы – применяются в том
случае, если признак не является по смыслу задачи вещественным числом; здесь
есть два существенно разных варианта:
¨
номинальные шкалы – применяются, если
целое число не является выражением какой-либо меры, а служит просто меткой
варианта ответа на вопрос; в случае если допустимыми вариантами ответа являются
только «да» и «нет», шкала называется бинарной
и признак принимает значение 1 или 0 ;
¨
порядковые или ординальные шкалы – применяются, если целое число отражает степень
проявления определенного качества (например, степень уверенности в ответе);
порядковая шкала может изменяться а) от одной противоположности до другой и
тогда допустимые значения располагаются симметрично относительно нуля – точки
неопределенности; б) от точки отсутствия качества до точки наивысшего его
проявления – и тогда естественно придавать признаку только положительные значения.
" относительно номинальных признаков
можно сделать следующее замечание – в литературе [1,19,34] встречаются
рекомендации разбивать любую номинальную шкалу на несколько бинарных, в
соответствии с присутствием или отсутствием какого-либо варианта ответа "
Исследователь должен прежде
всего четко представлять в каких шкалах измеряются те или иные признаки. Тип
шкалы может быть важен для ответа на вопрос исследователя: если два явления отличаются, то насколько сильно?
Выбор шкалы осуществляется не формальным образом, а только по смыслу
задачи. В примере с экономической таблицей число работающих на предприятии
может измеряться целым числом (если выбрать в качестве единицы измерения точное
число людей), однако признак по смыслу все равно измеряется в непрерывной шкале
(так, если измерять в тысячах, то признак начнет принимать дробные значения). С
другой стороны, можно превратить этот признак в ординальный, если разбить все
предприятия по категориям относительно числа работников (0 - малое, 1 -
среднее, 2 - крупное, 3 - сверхкрупное предприятие и т.п.).
Некоторые предварительные выводы
Итак,
предметом нашего исследования будут прежде всего таблицы данных, полученных в
результате наблюдения за изучаемой системой объектов или явлением. Еще раз
отметим, что само по себе построение таблицы предполагает, что исследованию
задано определенное направление, а об области исследования имеется какое-то
предварительное представление. Таким образом, уже на этапе собирания данных
делается первый шаг к абстрагированию от конкретной действительности, когда из
бесконечного числа способов описывать объекты исследования выбирается один,
характеризуемый выбором набора признаков, с помощью которого объекты отделяются
друг от друга.
За
собиранием данных следует их анализ, конечная цель которого – извлечение определенного
рода информации, или, более общо, знания из таблицы.
Как
видно из примеров, на практике в таблицах типа «объект-признак» число объектов
(строк таблицы) обычно измеряется тысячами, а число признаков (столбцов
таблицы) – сотнями. Естественно, что восприятие такого массива данных весьма
затруднено, а следовательно, затруднен и анализ. Графики или диаграммы способны
наглядно показать отношения лишь между двумя-тремя признаками, оставляя
остальные количественные характеристики за пределами внимания исследователя.
Таким образом, чем более признаков содержит таблица, тем, с одной стороны
полнее описываются объекты исследования, а с другой – тем труднее извлекать из
таблицы необходимую информацию.
Изложенные
далее методы и идеи будут направлены главным образом на то, чтобы создать у
исследователя некоторый целостный наглядный образ данных, с помощью которого он
мог бы ориентироваться в бесконечных полях чисел, собранных в больших таблицах.
Более того, в связи с
основной темой изложения нам будут неинтересны таблицы с числом столбцов менее
четырех, поскольку для таких таблиц вполне эффективно могут применяться
традиционные методы представления данных.
1.1.2. Представление данных
в абстрактном виде.
Первым шагом на
пути к созданию наглядного образа данных является представление объектов (строк
таблицы) в виде геометрических образов. При этом следует учесть несколько
возможных обстоятельств:
q
значения признаков, как правило, известны не
абсолютно достоверно, а с некоторой конечной точностью; разумеется, это замечание уместно в случае применения
непрерывных шкал признаков;
q
для значений некоторых признаков могут допускаться
определенные отклонения, величины которых устанавливаются здравым смыслом и
задачами исследования; в этом случае говорят, что данные измерены с
определенным допуском;
" не следует смешивать
понятия допуска и точности; точность – это отклонение от некоторого «истинного»
значения, определяемое возможностями измерительной аппаратуры, методикой
эксперимента и т.д., то есть внешними объективными причинами; допуск – это
такое отклонение, которым исследователь
намеренно пренебрегает, поскольку оно не играет значимой роли в его задаче, в
пределах этого отклонения исследователь считает любые два значения признака
совпадающими; естественно, что значение допуска, вообще говоря, не может быть
меньше точности "
q
информация об отдельных объектах может быть известна
не полностью, в этом случае говорят о данных, содержащих пробелы; при этом, как правило, на недостающие или недостоверные
значения признаков можно наложить некоторые априорные ограничения.
Упомянутые обстоятельства приводят к тому,
что отдельный объект из исследуемой совокупности данных может быть представлен
с помощью одного из следующих геометрических образов в некотором абстрактном
пространстве Rm ( m – число признаков объекта):
точкой – в случае если объект
характеризуется набором дискретных признаков, или считается, что все его
признаки известны с абсолютной точностью; координатами точки являются значения
соответствующих признаков;
m-мерной сферой или эллипсоидом – если задается погрешность
(или допустимое отклонение) положения объекта в абстрактном пространстве данных
относительно гипотетического точного положения;
m-мерным параллелепипедом –
если погрешность (или допуск) задаются отдельно для каждого из признаков;
отрезком прямой, параллельной одной
из координатных осей – если один из признаков неизвестен, а остальные известны
точно; длина отрезка отражает априорный допустимый диапазон, в котором может
находиться пропущенное значение;
куском k-мерной плоскости, если
пропущены k значений из набора
признаков объекта;
куском k-мерного слоя некоторой
толщины – если k значений
признаков в наборе пропущены, а остальные известны с некоторой точностью, при
этом толщина слоя отражает значение точности (или допуска).
После сопоставления каждому из объектов
геометрического образа в абстрактном многомерном пространстве данных возникает
облако из геометрических объектов, которое и отражает структуру исследуемого
набора данных. Изучая это облако, мы, тем самым будем изучать сами данные.
Однако, для того, чтобы говорить о геометрических отношениях внутри
облака данных, следует решить важный вопрос о выборе подходящей метрики для пространства. Не
определившись в этом вопросе, исследователь не может ответить на вопрос о том, насколько сильно по своим свойствам один
объект отличается от другого. От удачного выбора метрики часто зависит
насколько геометрическая метафора данных соответствует структуре самих данных.
Во второй главе нами будут рассмотрены
конкретные формулы для расчета расстояния между двумя объектами для некоторых
наиболее распространенных вариантов выбора метрики. Здесь же ограничимся
следующими качественными замечаниями:
q
достаточно очевидно требование того, чтобы
расстояние между объектами не зависело от того, меряем ли мы его от первого
объекта до второго или от второго к первому;
q
для правила вычисления расстояний должно
выполняться «неравенство треугольника»
(рис. 6), смысл которого состоит в том, что расстояние между двумя объектами
должно вычисляться в каком-то смысле по кратчайшей линии;
q

в случае если признаки
объекта принимают дискретные наборы значений, правило вычисления расстояния должно
быть соответствующим образом модифицировано для того, чтобы лучше
соответствовать специфике таких шкал признаков – так для порядковых признаков
часто применяется так называемая городская метрика, а для бинарных – расстояние
Хэмминга (рис. 7а и 7б)
1.2. Игры с
данными. Обряды и ритуалы.
1.2.1. Почему все так несерьезно?
Почему игры, обряды и ритуалы, а не просто
методы анализа? Речь пойдет о достаточно серьезных вещах, и о вполне работающих
методах работы с данными. Однако за
пределами любой методологии лежит опыт исследователя, который трудно или
невозможно формализовать. Прочитав учебник по математической статистике, можно
уяснить себе методологические основы анализа данных, но на практике всегда
окажется, что кроме того, что «надо делать, потому что это оправданно» есть еще
то, что «обычно делают, не особенно задумываясь». Словами психологов – «на
каждый полезный совет нужно еще тысяча о том, как его выполнить».
Это и составляет основу «обрядов» обращения с
данными. Обряд – это одновременно действия, оправданные с точки зрения строгой
методологии и то, что исследователь делает, не особенно задаваясь строгим
доказательством необходимости своих действий. Обряд состоит из ряда «ритуалов»
(один из ритуалов – обращение к строгим методическим принципам и терминам),
множество обрядов образуют формальные и неформальные правила игры с данными.
Ситуация эта не является специфичной для
прикладной статистики. В физике, например, практически невозможно формализовать
способы соотнесения реальному объекту его теоретической модели, в чем обычно
состоит сложность изучающих физику – общие принципы известны, но как «вставить»
в уравнения данное реальное явление – все это остается за рамками. Для того,
чтобы набраться неформального опыта учащийся решает большое число стандартных
задач, с помощью которых он уясняет как можно воплотить те или иные
теоретические принципы.
Приведем пример. Что делает исследователь в
первую очередь, если в руки ему попадает некоторый набор точек данных? Ответ
практически очевиден – считает среднее арифметическое координат этих точек и
дисперсию – разброс около среднего (либо, более общо, ковариационную матрицу).
Тем самым вычисляются достаточные статистики нормального распределения.
Исследователь, как правило, осознает, что распределение реальных данных может
оказаться далеким от нормального и среднее значение точек облака может
находиться вовсе вне области скопления данных, но делает это отчасти потому,
что «так положено», отчасти чтобы представить себе данные «в первом
приближении». Исследователь может оправдать себя тем, что, как и в физике, с
точки зрения «удаленного наблюдателя», облако данных выглядит как скопление
точек около их среднего значения. Они
примерно занимают область, соответствующую по объему шару с радиусом,
равным приблизительно квадратному корню из дисперсии (точки, выпадающие из этой
области будут практически незаметны для удаленного наблюдателя). В дальнейшем исследователь
может отбросить гипотезу о нормальном распределении как нереалистичную, но, тем
не менее, исследования данных начинаются с нее. Потому что таково предписание
ритуала, имеющего свою историю и основание.
Другой пример: дана таблица чисел 3х3 с одним
пропущенным значением:  . Задача: дать оценку пропущенного значения (задачи такого типа
составляют большую часть тестов на определение IQ – коэффициента умственного
развития). Первое, почти подсознательное, предположение – оценка равна единице.
Разумеется, что это предположение не выдерживает никакой критики с точки зрения
более или менее строгой методологии. Для статистического доказательства этой
гипотезы данных явно не достаточно. Однако, это значение является
правдоподобным. Поэтому, если нет никаких дополнительных соображений, но
пропущенное значение необходимо как-то восстановить, то разумно предположить,
что оценка равна не нулю, и не тысяче, а именно единице, что тоже составляет
часть ритуала. С другой стороны, это значение вовсе не является необходимым.
. Задача: дать оценку пропущенного значения (задачи такого типа
составляют большую часть тестов на определение IQ – коэффициента умственного
развития). Первое, почти подсознательное, предположение – оценка равна единице.
Разумеется, что это предположение не выдерживает никакой критики с точки зрения
более или менее строгой методологии. Для статистического доказательства этой
гипотезы данных явно не достаточно. Однако, это значение является
правдоподобным. Поэтому, если нет никаких дополнительных соображений, но
пропущенное значение необходимо как-то восстановить, то разумно предположить,
что оценка равна не нулю, и не тысяче, а именно единице, что тоже составляет
часть ритуала. С другой стороны, это значение вовсе не является необходимым.
Итак, применение каждого метода на практике
сопровождается определенным ритуалом, включающего действия с данными,
необходимость (и достаточность) которых невозможно строго вывести из самого
метода. Важную часть ритуала составляют «заклинания» – устойчивые словесные
формулировки, которыми сопровождается ритуал.
Заклинания можно разделить на рекламные
(«этот метод делает что-то, что не делают другие») и технологические («мы
сделали это, потому что это вытекает отсюда»). Рекламные заклинания, вроде
«нейросети могут все», «метод главных компонент максимально сохраняет структуру
расстояния между точками данных» или «самоорганизующиеся карты Кохонена
сохраняют топологические особенности набора данных» являются эффективным
средством выделить метод среди аналогичных и продвигать его на конференциях,
давая обещания его потенциальным пользователям. От удачной формулировки
рекламного заклинания может зависеть судьба метода. В рекламных заклинаниях,
как правило, нет прямого обмана, но к таким заклинаниям всегда следует
относиться осторожно, поскольку выполнение обещания всегда сопровождается
определенными оговорками. Лучше быть заранее в курсе условий применения метода,
чем выяснять их самостоятельно, на своем «печальном опыте».
Технологические заклинания призваны создать у
слушателя или читателя впечатление того, что исследователь на своем пути строго
следует логически оправданным методологическим установкам. Хотя, как правило,
реальный путь исследования оказывается слишком извилистым, чтобы рассказывать о
нем в подробностях. Технологические заклинания полезны, потому что они «спрямляют»
этот путь, но и к ним необходимо относиться с осторожностью. Во-первых,
существенная часть таких заклинаний делается «задним числом» (раз это сработало
– значит это верно), а во-вторых, они могут скрадывать некоторые существенные
детали исследования. Характерная ситуация в статистике, когда без технологических
заклинаний не обойтись: это обработка «аномальных наблюдений» – объектов из
набора данных, которые ни каким образом не укладываются в построенную модель.
Такие данные либо уточняются, либо «ремонтируются» (тоже по определенному
ритуалу со своими заклинаниями), либо просто уничтожаются (по ритуалу вывода из
игры «недостоверных» наблюдений). Неосторожное обращение с технологическими заклинаниями
может легко подорвать у пользователя доверие к методу. Наверняка именно оно
стало причиной появления мнения о том, что «есть три вида лжи: ложь, наглая
ложь и статистика». Если исследователь не желает, чтобы его метод заработал
против него самого, он должен с величайшей аккуратностью формулировать
технологические заклинания.
Мы не претендуем на то, что в этой книге
читатель найдет ясное и подробное описание всего набора ритуалов, необходимых
для применения изложенных методов, и тексты заклинаний, хотя при желании он
может извлечь и то, и другое. Цель нескольких последних абзацев – предупредить
неискушенного читателя, с чем он неизбежно столкнется на практике, чего
необходимо опасаться. Читатель предупрежден – и мы следуем дальше.
1.2.2. О происхождении данных[1].
Можно сказать, что в выбранной системе признаков
таблица данных содержит описание объектов или функционирования системы с
максимально возможной полнотой. Тем не менее, исследователю требуется не
столько полное знание всего массива информации, сколько определенного рода
«сухой остаток». Для того, чтобы делать выводы, он должен иметь возможность как
то представить себе данные: что в них более, а что менее существенно, какие
тенденции в них присутствуют. Тогда он будет способен содержательно о них
рассуждать, сравнивать с другими системами объектов (возможно, отыскивая при
этом полезные аналогии), делать правдоподобные предсказания о возможных
качествах новых объектов, которые могут появиться в системе.
Таблицу данных можно воспринимать как прямое
описание фрагмента действительности – «такой, как она есть». Для того, чтобы
извлечь пользу из этого описания (например, создать математическую теорию этого
фрагмента), исследователь должен использовать метод представления
действительности в форме, удобной для оперирования и осмысления. Такой метод,
давно закрепившийся в естественных науках, называется моделированием. Создание моделей действительности служит
обязательным промежуточным звеном в связывании теории с положением вещей «как
оно есть». Абстрактная теория не может описывать действительность напрямую, она
лишь указывает на определенные отношения между абстрактными объектами в
абстрактном мире (например, теория утверждает, что коммутатор двух определенных
матриц всегда равен числу). В модели реализуется способ интерпретации теории,
то есть способ сопоставления реальным объектам абстрактных. Одна и та же теория
может рождать разные модели, относящиеся к совершенно различным фрагментам
действительности. Более того, одна и та же теория может рождать разные модели
одного и того же объекта.
Таким образом, модель – промежуточный шаг на
пути от прямого описания действительности к ее абстрактному описанию. При
решении поставленной задачи исследователь неоднократно проходит этот путь как в
одном, так и в другом направлении.
Из всего множества функций, которые могут выполнять
модели, можно выделить две основных. Во-первых, модель служит удобной заменой
объектов действительности, своеобразным «аккумулятором знаний» об объекте. С
помощью модели можно имитировать функционирование системы и прогнозировать ее
поведение в эмпирически недоступных условиях, то есть так или иначе расширять
полученный опыт. Во-вторых, модели могут играть смыслообразующую роль, то есть
давать толчок к рождению новых смыслов, понятий, терминов в системе научного
знания, которые могут быть использованы для качественно нового описания
изучаемого фрагмента действительности.
Какое место занимают модели данных во всем многообразии встречающихся в науке моделей? В
[8] изложена классификация моделей по 8-ми типам. Она, в свою очередь, основана
на предложенной Р.Пайерслом классификации моделей в современной физике. Будем
считать, что аналогичное положение вещей наблюдается во всех областях естественнонаучного
знания.
Перечислим предложенные восемь типов моделей.
К каждому из названий прилагается краткая характеристика, описывающая
методологическую позицию исследователя (заметим, что эти характеристики –
пример своего рода технологических заклинаний).
1. Гипотеза (такое могло бы быть).
2. Феноменологическая модель (ведем себя, как
если бы).
3. Приближение (что-то считаем очень малым
или очень большим).
4. Упрощение (опустим для ясности некоторые
детали).
5. Эвристическая модель (количественного
подтверждения нет, но модель способствует более глубокому проникновению в суть
дела).
6. Аналогия (учтем только некоторые
особенности).
7. Мысленный эксперимент (главное состоит в
опровержении возможности).
8. Демонстрация возможности (главное –
показать внутреннюю непротиворечивость возможности).
Теперь покажем какие модели из этого
«зоопарка» в основном населяют мир прикладной статистики. Большая часть
учебников заполнена моделями первого типа. При этом существуют два основных
варианта:
1. Модели,
основанные на гипотезе о статистическом происхождении данных.
Эта гипотеза подразумевает, что набор данных
является выборкой из бесконечной генеральной
совокупности объектов, чье распределение подчиняется определенному вероятностному
закону. Более того, эта выборка должна быть сформирована независимым случайным выбором
объектов генеральной совокупности. Принятие этой гипотезы (в реальных ситуациях
весьма сильной) дает возможность со спокойной совестью применять к данным
теоретико-вероятностные подходы, то есть фактически моделью такого набора
данных является вся генеральная совокупность (данные дополняются до
бесконечного числа объектов) с ее законом распределения.
Реальная практика эксплуатации этой гипотезы,
как правило, приводит к тому, что исследователю приходится прибегать к
определенного рода лукавству. Дело в том, что для того, чтобы иметь
по-настоящему «спокойную совесть», корректность принятия (с хорошей
достоверностью) гипотезы требуется строго доказать (по определенному ритуалу, который
подробно описан в разделе математической статистики о проверке статистических
гипотез). «Проклятием» большинства статистических исследований (в медицине,
биологии, экономике, гидрологии и пр.) является то обстоятельство, что строгого
доказательства провести не удается (как правило, просто недостаточно данных), и
степень достоверности гипотезы может вызывать сомнение. Но поскольку в руках
исследователя часто просто не оказывается других инструментов, он вынужден все
равно принимать малодостоверную гипотезу. Это приводит его к созданию модели
типа 2 (феноменологическая модель), которая отличается от первой по сути лишь
разной степенью достоверности.
2. Модели,
основанные на гипотезе о порождении данных динамическим законом.
Согласно общей установке законы природы
делятся на динамические и статистические. Считается, что первые выполняются
со всей необходимостью (содержат детерминированные правила), вторые выполняются
лишь «в среднем». Большинство законов в природе не являются ни чисто
динамическими, ни чисто статистическими. «Лучшими» в свое классе
представителями динамических законов можно назвать законы небесной механики
(именно поэтому положения космических объектов в Солнечной системе могут быть вычислены
с большой точностью и практически из первых принципов), для статистических
законов в качестве хорошего примера можно указать на закон распределения
вероятности появления электрона в квантовомеханической модели атома водорода.
Можно сделать предположение о том, что данные
имеют не статистическую природу, а получены как результат детерминированного
функционирования определенной системы, но, возможно, с наложением различного
рода флуктуаций, которые, в свою очередь, могут быть описаны статистическими
законами. Выбор конкретного вида динамического закона осуществляется исходя из
априорных соображений, положений других теорий, интуиции исследователя и т.п.
Этот закон может не носить на себе никаких следов физического осмысления
механизмов системы (например, исследователь решает: данные распределены «по
закону параболы» при наличии шума, который имеет нормальное распределение с
дисперсией, которую можно оценить из имеющихся данных).
Зачастую, принимая гипотезу о динамическом
законе, исследователь не в состоянии даже оценить ее достоверность. Поэтому
почти все такие модели оказываются ближе ко второму типу (феноменологическая
модель).
Итак, существенная часть моделей прикладной
статистике основана на тех или иных гипотезах о природе происхождения данных:
динамической и статистической. И та, и другая гипотеза заставляет исследователя
догадываться о том, что стоит за данными, что их породило, и каковы свойства
этого «нечто». В результате исследователь привязывает свои данные к тем
существующим модельным системам, свойства которых ему лучше всего известны.
Можно ли без этого обойтись?
Альтернативой производству гипотез является
описание данных «как есть». В принципе, исследователь может представлять себе,
что данные порождены некоторой системой (иногда эту систему можно даже
«пощупать руками»: например, контейнер для хранения промышленных отходов, как в
статье [44]), но он исходит из того, что внутреннее устройство этой системы ему
неизвестно из-за высокой сложности и многокомпонентности. Ему проще описывать
сами данные, отражающие работу системы в тех или иных условиях, чем создавать
ее динамическую модель. Такой тип моделей может быть назван информационными.
Основным принципом информационного
моделирования является принцип «черного ящика» – моделируется не внутреннее, а
внешнее функционирование системы. Такие модели по общей классификации могут
быть отнесены к 4 типу (упрощение). При этом упрощение необходимо понимать
следующим образом: исследователь понимает при создании модели, что реальная
система качественно более сложна, чем любая известная теоретическая модель, и
для того, чтобы как-то ухватить это качество сложности, он описывает систему
так, как она проявляет себя для внешнего наблюдателя. В каком-то смысле
исследователь соглашается с тем, что набор данных о системе и сама система
эквивалентны, упрощая при этом, разумеется, реальное положение дел.
В способе построения информационных моделей
есть свои преимущества и недостатки. Несомненным преимуществом является
принципиальная возможность моделирования (причем не наукоемкого моделирования)
сколь угодно сложных систем. Недостатками являются низкая «объяснимость»
результатов, выдаваемых моделью, и привязка модели к конкретной системе (часто
бывает, что опыт, накопленный на одном объекте, в выбранной системе
признаков-свойств будет неадекватен опыту, накопленному на другом, вполне аналогичном
объекте).
" Упоминания заслуживает
пригодность информационных моделей для количественно точных оценок
прогнозируемых явлений. Изначально, информационная модель строится именно с
целью точного или почти точного описания действительности, то есть задаваемого
набора данных. Вместе с тем информационная модель должна обладать
предсказательными (обобщающими) способностями для того, чтобы иметь возможность
правдоподобно прогнозировать свойства новых, не участвовавших в настройке
модели объектов. Отдельным направлением являются методы автоматического
извлечения знаний из информационных моделей. Модели, подвергнутые подобным
процедурам, могут быть отнесены в разряд эвристических моделей (тип 5). Они
могут обладать худшими способностями к количественным предсказаниям за счет
увеличения «объяснимости» получаемых результатов. Подробнее об этом можно
познакомиться в [48] "
В упомянутой работе [44] предлагается
следующая типология информационных моделей по их предназначению:
q
Моделирование отклика системы на внешнее воздействие
q
Классификация внутренних состояний системы
q
Прогноз динамического изменения системы
q
Оценка полноты описания системы и сравнительная
информационная значимость параметров системы
q
Оптимизация параметров системы по отношению к
заданной целевой функции
q
Адаптивное управление системой
Предлагаемые в этой книге способы построения
информационных моделей могут применяться для любой из поставленных выше целей –
достаточно лишь разработать соответствующий ритуал на базе предлагаемого
метода. Однако, главной целью создания двумерных информационных моделей является
q
Визуализация многомерной структуры данных
Преследуя эту цель, мы, с одной стороны,
ограничиваем метод в точности (хотя нами предлагаются и способы практически
неограниченного увеличения точности описания), с другой – даем возможность
исследователю создать себе наглядный образ набора данных, с помощью которого он
сможет анализировать их структуру, практически не прибегая к сторонним методам.
Итак, нашей основной целью является создание
двумерных информационных моделей. Но прежде всего дадим краткий обзор
традиционных методов анализа данных, классифицируя эти методы по тем вопросам,
на которые они могут дать содержательный ответ.
1.2.3. Вопросы которые мы
ставим, глядя на данные…
Как уже упоминалось, основная цель анализа данных –
извлечение из них информации. То, в каком виде будет представлена извлеченная
информация – зависит главным образом от двух обстоятельств – а) от задач и
целей исследования; б) от характера и качества тех процедур извлечения
информации, которые исследователь имеет в своем распоряжении.
" В отличие от неопределенного, интуитивно
постигаемого понятия данных, термин информация,
содержащаяся в данных определен несколько точнее. Существует два основных
подхода к понятию информации.
Первый
из них связан с именем К.Шеннона и лежит в основе раздела кибернетики – теории
информации. Согласно этому подходу, количество информации содержащееся в одном
случайном объекте (событии, величине) относительно другого случайного объекта может быть измерено
положительным числом. Пусть x – случайная величина,
принимающая значения x1, x2 … xn с
вероятностями p1, p2 … pn, а h – случайная величина, принимающая значения y1, y2 … yn с
вероятностями q1, q2 … qn. Тогда количество информации, содержащееся в x относительно h равно ![]() , pij – вероятность совмещения
событий x = xi и h = yj. В случае, если x и h – величины независимые, то I(x,h) = 0.
Имеет место неравенство I(x,h) £ I(h,h), причем равенство достигается
только в случае, если h является точной функцией от
x (например, h = x2).
, pij – вероятность совмещения
событий x = xi и h = yj. В случае, если x и h – величины независимые, то I(x,h) = 0.
Имеет место неравенство I(x,h) £ I(h,h), причем равенство достигается
только в случае, если h является точной функцией от
x (например, h = x2).
С
понятием информации тесно связано понятие энтропии
случайной величины. Так энтропия x, по определению равна ![]() . Смысл энтропии – среднее число двоичных знаков, необходимое
для различения (или записи, кодирования) возможных значений случайной величины.
. Смысл энтропии – среднее число двоичных знаков, необходимое
для различения (или записи, кодирования) возможных значений случайной величины.
Второй
подход к понятию информации существует в математической статистике, в теории
статистических оценок, и предложен Р.Фишером. В данном подходе вводится понятие достаточных статистик – набора функций от данных, с помощью
которых можно полностью восстановить
характер исходного распределения данных в пространстве. Так, для
нормального распределения достаточными
статистиками являются среднее арифметическое и выборочная дисперсия. В
статистике говорят, что знание этих величин дает полную информацию о
распределении данных (то есть является их лаконичным описанием).
Соответственно, знание не полного набора достаточных статистик дает частичную
(неполную) информацию о распределении данных, и количество этой информации
может быть выражено некоторой мерой. Напомним, что для статистических подходов
существенно принятие статистической
гипотезы о наличии генеральной
совокупности, подчиненной определенному статистическому
закону. "
Разумно предположить, что интуитивно под информацией
исследователь подразумевает некоторое описание данных, которое по своей длине,
по крайней мере, не превосходит простое перечисление тех значений, которое
принимают признаки объектов. То есть в качестве конечного результата применения
технологий извлечения информации исследователь желает получить по возможности лаконичное, наглядное и полезное
описание данных. Итак, один из основных тезисов нашего изложения –
ü Анализ данных –
это наглядное, лаконичное и полезное их описание ü
Попробуем
перечислить основные моменты общепринятых на сегодня технологий анализа данных.
Для этого сформулируем ряд вопросов, которые исследователь традиционно задает
себе во время применения процедур анализа, и из ответов на которые постепенно
складывается упомянутое выше описание данных. Последовательность таких вопросов
составляет определенный ритуал, в котором используются исторически устоявшиеся
термины и формулировки («заклинания»). Общность языка позволяет разным исследователям
сравнивать результаты своего анализа.
Итак,
проанализировав набор данных, исследователь должен быть готов ответить на
следующие общие вопросы:
q
Стоит ли
что-нибудь за данными и как оно устроено?
В основе
подавляющего большинства методов математической статистики лежит гипотеза о том, что набор данных представляет
из себя независимую выборку из некоей
генеральной совокупности – бесконечного набора точек, плотность распределения
которых строго подчинена определенному закону. Ответ на заданный вопрос
подразумевает указание на вид закономерности, соответствующей генеральной
совокупности и правдоподобную оценку ее параметров. Соответствующие технологии
составляют основу параметрических методов теории статистических оценок. Знание
всех необходимых параметров (достаточных статистик) дает полную информацию о
наборе данных в случае принятия основной статистической гипотезы.
Другим видом
гипотезы является предположение о динамическом законе порождения данных.
Однако
исследователь волен подвергнуть сомнению разумность гипотез о существовании
генеральной совокупности или динамических законов и вовсе отказаться от них, утверждая,
что за данными не стоит ничего, кроме них самих. Соответствующая концепция
может быть названа гипотезой об автоинформативности
набора данных. В этом случае исследователь занимается прямым описанием самого
облака данных и применяет для этого соответствующие технологии.
Своеобразным
компромиссом между противопоставленными выше подходами является применение
непараметрических статистических методов. В этом случае по прежнему
предполагается наличие генеральной совокупности, но считается, что ее
особенности не могут быть описаны простыми формулами с разумным количеством
параметров. В этом случае с помощью набора данных в каждой точке пространства
оценивается плотность распределения точек – создается непараметрическая модель
генеральной совокупности. Иначе можно сказать, что плотность распределения
точек генеральной совокупности оценивается с помощью общих формул, в которые в
качестве параметров входит сразу весь набор данных (а не отдельные статистики,
из них образованные). Существует несколько подходов для такого оценивания – со
своими достоинствами и недостатками, и о них вкратце будет упоминаться во
второй главе.
q
Возможно ли
построить на множестве данных сколько-либо разумную (естественную, полезную)
систему отношений?
Здесь мы, прежде
всего, подразумеваем применение всего семейства методов, связанных с классификацией, кластерным анализом, таксономией
данных и т.д.
Решение задач
классификации составляют основную цель применения методов теории распознавания
образов. В задаче классификации с
учителем отношения на системе объектов заданы изначально, требуется
экстраполировать эти отношения на все пространство данных – отнести каждую из
точек пространства данных к определенному классу при помощи классификационного или решающего правила, построенного при
помощи набора данных (или его подмножества), в котором каждой точке заранее
сопоставлена метка класса. В этом случае те данные, классификация которых
заранее известна, называются обучающим
множеством (задачником). Как правило, той информацией, которая извлекается
из данных в данном подходе является указание на вид решающей функции, или вид решающих
поверхностей, отделяющих пространственно один класс от другого.
При классификации без учителя разбиение
множества на классы осуществляется в результате решения задачи на оптимизацию
некоторого критерия (например, критерия близости точек, принадлежащих каждому
из классов к их центроиду –
«типичному представителю» класса). В этом случае возможны два варианта, когда
а) число классов
известно заранее, и тогда извлеченной из данных информацией является
разбиение множества данных на заданное число классов эквивалентности,
положения центроидов в пространстве данных, меры близости точек одного класса к
их центроиду, меры удаленности одного класса от другого и т.д.;
б) число классов
заранее неизвестно, и тогда к извлеченной информации добавляется количество
классов (кластеров данных, точек сгущения), и, в конечном итоге, данные описываются
как иерархия классов эквивалентности
(например, все данные разбиваются на три класса, в каждом из них есть свое
разбиение на подклассы и так далее).
q
Какова
эффективная размерность множества данных?
Извлечение
информации при ответе на данный вопрос, как правило, ведется в двух
направлениях (впрочем, не вполне независимых друг от друга): а) поиск
многообразия меньшей размерности, вложенного в пространство данных, вдоль
которого данные располагаются достаточно тесно; б) выделение группы наиболее информативных признаков, с
помощью которых с заданной точностью можно было бы восстановить значения остальных,
и определение зависимостей, связывающих признаки.
Естественным
критерием при поиске многообразия, моделирующего или аппроксимирующего данные, является требование минимизации среднего
расстояния от точки данных до ближайшей точки многообразия. На практике одного
такого требования оказывается недостаточно (если минимизировать только указанную
величину, то полученное многообразие может обладать совершенно неприемлемыми
свойствами). Например, многообразие может представлять из себя ломанную в произвольном
порядке соединяющую все точки данных – тогда среднее расстояние равно нулю.
При анализе
«номенклатуры» признаков существуют несколько подходов.
Во-первых, это
анализ значимости той или иной группы
признаков относительно определенного критерия. Критерий формируется исходя из
задаваемого «руками» вида зависимости, которая будет связывать одни признаки с
другими (например, линейная связь). Задача состоит в том, чтобы указать
минимальный поднабор признаков, с помощью которого, используя признаки как
независимые переменные, с указанной точностью можно было бы восстановить
значения других признаков при заданном виде зависимости. Простейший из способов
– полный перебор сочетаний признаков – неприемлем с точки зрения вычислительных
затрат уже для таблиц с несколькими десятками столбцов, поэтому для определения
такого поднабора существует довольно обширный арсенал эвристических приемов.
Если указан
поднабор наиболее значимых признаков, то менее значимые признаки могут быть
вообще удалены из рассмотрения, как лишенные информативной нагрузки (однако, если
не сказано явно, всегда нужно мысленно добавлять – «в переделах заданной
точности или допуска»).
Другой подход лежит
в основе методов факторного анализа.
Признаки объектов в этом случае представляются в виде комбинаций (линейных или
других) меньшего числа других, непосредственно не измеряемых (скрытых,
латентных) факторов. Факторы обычно конструируются так, чтобы они оказались
взаимно некоррелированными. Число факторов с помощью которых удается свести
погрешность описания – остаток, к приемлемому уровню и является эффективной
размерностью пространства в этой модели.
В итоге, следуя
тому плану, который набросан в отмеченных общих вопросах, исследователь
описывает рассматриваемые данные (рассказывает о них) в терминах того или иного
подхода. В результате у него складывается некоторое внутренне представление о
структуре набора данных и о зависимостях, присущих данным. Причем, и это
существенно для нашего изложения, следует отметить, что точные количественные
характеристики, извлеченные с помощью разных подходов, играют второстепенную
роль по сравнению с возникающим
качественным представлением о наборе данных. Не столько конкретные
числа, сколько наглядный образ позволит исследователю приступить на следующем
этапе к созданию теоретической модели, обобщающей особенности изучаемой системы
и обладающей способностью к прогнозу качественных и количественных
характеристик для новых объектов, появляющихся в системе.
1.2.4. …и ответы, которые мы
можем получить.
Равномерное и нормальное
распределения
Стоит уделить внимание двум самым простым,
традиционным и тщательнейшим образом изученным моделям данных – равномерному и
нормальному распределениям. Трудно переоценить их роль для современного
состояния практически любой из наук, имеющей дело со статистическими оценками,
где либо одно, либо другое выступают в роли или базовых моделей, или начальных
приближений, или предельных случаев.
Для того, чтобы избежать путаницы, сразу
обратим внимание на то, что понятие выборки
и распределения
существенно отличны. Независимая выборка из генеральной совокупности – это
конечное множество точек данных, полученных в результате случайного выбора
точек из генеральной совокупности. Распределение – это закон сопоставления каждой
бесконечно малой области пространства вероятности появления в ней точки данных.
Выборка дискретна, а распределение, как правило, кусочно-непрерывно.
Можно сказать, что равномерное распределение
выражает идею равновозможности исходов в случае непрерывных случайных величин.
Тогда вероятность принятия случайной величиной значения в произвольной точке
фазового объема везде одинакова и обратно пропорциональна величине объема.
" Непрерывное равномерное
распределение можно получить из дискретного, например, следующим образом.
Возьмем бесконечный набор случайных величин Z1, Z2 … Zn, принимающих значения 0 и 1 с вероятностью ½. Если мы построим непрерывную случайную
величину ![]() (фактически
формула дает способ представления числа из диапазона [0,1] в двоичной форме), то
ее распределение будет равномерным на отрезке [0,1].
(фактически
формула дает способ представления числа из диапазона [0,1] в двоичной форме), то
ее распределение будет равномерным на отрезке [0,1].
Другой
пример равномерного распределения – если из произвольных независимых
непрерывных случайных величин X1, X2 … Xn образовать сумму
sn = X1 + X2 … + Xn , то в пределе n ® ¥ дробная
часть sn будет распределена
равномерно на отрезке [0,1)."
Допустим, исследователь решил, что данные в
пространстве распределены равномерно (то есть, например, являются выборкой из
генеральной совокупности с равномерным законом распределения). Это
соответствует ситуации, когда «все возможно» – то есть в системе может
существовать объект или явление с любым из допустимых набором свойств с равной
вероятностью.
Каким образом тогда исследователь может
описать свои данные – то есть каковы будут его ответы на заданные выше вопросы?
Надо сказать, что ответы эти будут максимально (из всех возможных моделей) бедны. То есть, если
данные распределены в пространстве равномерно, то в облаке данных нельзя
выделить никакой естественной структуры (нет ни кластеров, ни точек сгущения),
в облаке нет выделенных направлений, и эффективная размерность множества данных
совпадает с размерностью пространства, то есть нет никаких значимых связей
между признаками объектов. Таким образом, равномерное распределение является
наименее емким с точки зрения содержащейся в нем информации.
" С помощью простого расчета
можно показать, что равномерное распределение соответствует максимальной
энтропии случайной величины.
В
статистической физике максимум энтропии пространственного распределения молекул
соответствует равновесному (устойчивому) состоянию системы. "
Если для модели равномерного распределения характерно
«отсутствие» информации в наборе данных, то модель нормального распределения является
простейшим случаем, когда в наборе данных содержится информация,
сформировавшаяся «стихийно», то есть если исследуемая система объектов
находится под воздействием большого числа независимых случайных факторов,
каждое из которых изменяет свойства-признаки объектов в определенном направлении, но среди этих факторов нельзя
выделить «главного», чье воздействие на систему было бы несопоставимо по
масштабу в сравнении с суммой всех остальных воздействий (то есть действие
любого фактора может быть полностью скомпенсировано либо другим, либо суммой
нескольких факторов).
" Термин нормальное распределение был введен К.Пирсоном. Однако сам вид и
свойства распределения подробно изучались, начиная с Гаусса. На сегодняшний
день нормальное распределение является наиболее теоретически изученной и
практически применяемой статистической моделью. Она возникает в качестве
основной в огромном количестве естественнонаучных приложений.
Нормальное распределение может быть
получено как предел дискретного биномиального распределения при большом
количестве испытаний. Соответствующий результат оформлен в виде теоремы Муавра-Лапласа.
Полное
теоретическое исследование исключительной роли нормального распределения было
закончено только в тридцатый годах двадцатого столетия. Обоснование такой
исключительности дается в предельных
теоремах теории вероятностей. Утверждение центральной предельной теоремы состоит
в том, что для последовательности X1, X2 … Xn независимых случайных величин отклонение суммы sn = X1 + X2 … + Xn от своего математического
ожидания M(sn)=M(X1)+M(X2)+…+M(Xn)
подчиняется нормальному закону распределения в пределе n ® ¥ .
Условия применения центральной предельной теоремы даются в теореме Ляпунова (основной вывод теоремы – среди
последовательности X1, X2 … Xn не должно быть величин, имеющих
больших значений моментов по сравнению с общей дисперсией суммы sn).
Интересной
особенностью нормального распределения является то, что сумма нормально
распределенных величин также распределена нормально. Для равномерного
распределения аналогичного утверждения сделать нельзя. Сумма нескольких
равномерно распределенных величин не является равномерно распределенной, но
распределение такой суммы быстро стремится к нормальному при увеличении числа
слагаемых. "
Допустим, что облако
объектов «похоже» на выборку из генеральной совокупности, подчиненной закону
нормального распределения (уточнению понятия «похоже» посвящена литература по
проверке статистических гипотез, например [4,29], здесь мы не будем вдаваться в
тонкости этой серьезной науки). Попробуем дать описание распределения точек
данных в пространстве. Данные представляют собой один кластер, имеют одну точку
сгущения (унимодальная плотность) в
точке среднего арифметического значений всех признаков. Чем ближе к этой точке,
тем выше плотность распределения объектов. Более 60% всех объектов находятся в
области, представляющей собой эллипсоид, центрированный в точке сгущения с
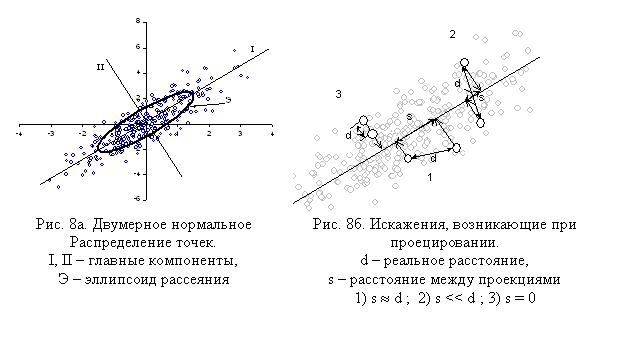
осями, равными собственным значениям так называемой ковариационной матрицы (эллипсоид рассеяния, подробнее об этом
во второй главе, см. рис. 8).
Обратимся теперь к анализу
эффективной размерности. Прежде всего, ответим на следующий вопрос: что из себя представляет линия, для которой
среднее квадрата расстояния от нее до точек данных минимально?
Сразу следует отметить
– если мы не накладываем никаких дополнительных ограничений на регулярность[2]
этой линии, то подойдет любая ломаная, соединяющая точки данных в произвольном
порядке. Поступим иначе и потребуем, чтобы эта линия была максимально регулярной,
пусть это будет прямая.
Назовем такую прямую первой
из главных компонент. Она проходит
через центр облака и ориентируется вдоль наибольшей вытянутости (дисперсии) облака данных (см. рис. 8а).
Это направление совпадает с направлением наибольшей по длине оси эллипсоида рассеяния.
Значения координат вектора,
задающего направление первой из главных компонент, являются количественными
мерами значимости признаков. Чем меньше значение соответствующей координаты,
тем менее значим и информативен признак. Этот же вектор является фактором для
простейшей однофакторной модели набора данных с распределением, «похожим» на
нормальное. В этом смысле знание координат этого вектора является самой
существенной долей извлеченной из набора данных информации, причем тем более
существенной, чем длиннее большая из осей эллипсоида рассеяния по сравнению с
остальными. Первая из главных компонент позволяет приближенно восстановить
значения всех признаков, если известно значение только одного из них.
Если точность такого
моделирования данных оказывается недостаточной, то определяется направление
второй из главных компонент. Из векторов, соответствующих каждой точке данных
вычтем вектор ортогональной проекции
точки на первую главную компоненту. Назовем новый полученный набор
векторов множеством первых остатков.
Построим в этом множестве первую главную компоненту. Ее направление окажется
направлением второй главной компоненты для исходного множества. Это будет
прямая, проходящая через центр распределения, перпендикулярно к первой из главных
компонент, совпадающая с направлением второй из главных полуосей эллипсоида
рассеяния.
На полученные два вектора можно натянуть плоскость первых двух главных компонент.
Среди всех плоскостей эта плоскость обладает свойством минимума суммы квадратов расстояний от нее до точек данных. С
помощью нее можно а) построить двухфакторную модель данных; б) восстановить
значения признаков объекта, если известны значения двух признаков; в) простым образом визуализировать многомерные данные, спроецировав каждую точку
данных ортогонально на плоскость первых двух главных компонент.
Остановимся несколько подробнее на последнем моменте.
Процедура ортогонального проецирования точки на плоскость задает отображение из
исходного пространства большой размерности Rm в пространство R2, то есть сопоставляет
каждой точке исходного пространства две координаты на плоскости. Среди всех
отображений типа ортогонального проецирования на плоский экран такое отображение будет оптимальным по отношению к
сохранению структуры расстояний между точками в исходном пространстве. Если же
бы мы имели дело с бесконечным числом объектов генеральной совокупности,
подчиненной нормальному закону распределения, то такое отображение было бы
оптимальным среди любых отображений из Rm в R2.
Здесь мы впервые касаемся основного вопроса нашего
изложения – зачем же нужно
визуализировать данные? Дело в том, что было бы очень полезно иметь
возможность представить многомерное облако данных в виде наглядной двумерной
картинки, то есть снизить размерность облака до двух измерений, но таким образом,
чтобы на полученном изображении некоторым оптимальным образом были видны
основные закономерности, присущие набору данных: его кластерная структура,
изначальное разделение данных на классы (если таковое имеется), существование
различных зависимостей между признаками и так далее. Вообще, если исследователь
будет иметь возможность хоть как-то наглядно представить себе многомерное
облако данных, многие задачи анализа (то есть в конечном итоге – описания
данных) решаются с помощи непосредственного зрительного восприятия картины
множества объектов.
Итак, наиболее приемлемым способом визуализировать набор
точек данных, чье распределение «похоже» на выборку из нормальной генеральной совокупности,
является ортогональное проецирование на плоскость первых двух главных
компонент. Плоскость проектирования является, по сути плоским двумерным «экраном»,
расположенным в пространстве таким образом, чтобы обеспечить «картинку» данных
с наименьшими искажениями. Такая проекция будет оптимальна (среди всех
ортогональных проекций на разные двумерные экраны) в трех отношениях:
1) Минимальна сумма
квадратов расстояний от точек данных до проекций на плоскость первых
главных компонент, то есть экран расположен максимально близко по отношению к
облаку точек.
2) Минимальна сумма
искажений расстояний между всеми парами точек из облака данных после
проецирования точек на плоскость. Поясним это подробнее. Возьмем любую пару
точек в исходном пространстве. Между ними есть какое-то ненулевое расстояние.
После проецирования каждой из точек на плоскость главных компонент расстояние
между проекциями будет уже иным (см. рис. 8б) – в некоторых случаях оно может
даже оказаться нулевым – для разных точек проекции могут совпасть, если они
лежат на одной прямой, перпендикулярной плоскости проецирования. Можно ввести
меру искажения расстояния между точками после проецирования (например,
относительную погрешность). Утверждается что при использовании плоскости первых
двух главных компонент сумма этих искажений достигает минимума (разумеется,
если точек достаточно много).
3) Минимальна сумма
искажений расстояний между всеми точками данных и их «центром тяжести», а также
сумма искажений углов между векторами, соединяющими точки и «центр тяжести».
В случае нормального распределения центр тяжести распределения совпадает с
точкой сгущения – геометрическим центром распределения и средним
арифметическим значений признаков всех объектов.
I Пример.
Проецирование данных на плоскость 1-ой и 2-ой главных компонент.
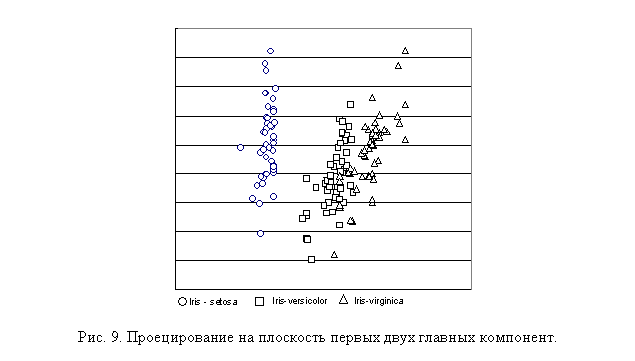
На рис. 9 показана проекция
четырехмерного облака точек данных, соответствующей реальной таблице данных,
собранных в результате измерения ботанических классификационных признаков трех
различных видов цветка ириса. Эта база данных традиционно используется в
литературе в качестве иллюстраций при испытании различных алгоритмов анализа
данных. В таблице представлено по 50 результатов измерений для каждого вида
цветка. В качестве координат четырехмерного пространства использовались длина и
ширина лепестка цветка, и длина и ширина чашелистика цветка. Из рисунка видно,
что, используя метод главных компонент, можно уверенно отделить класс Iris-setosa
от двух других классов, в то время как классы Iris-versicolor
и Iris-virginica остаются
перемешанными.
Возникает естественный вопрос – а как обстоит дело с наборами данных,
которые не могут считаться выборками из генеральной совокупности с нормальным
распределением? Перечисленные свойства плоскости главных компонент сохраняются
для произвольного облака точек при
условии, что рассматривается визуализация (проецирование) только при помощи
двумерных линейных многообразий
(различным образом ориентированных в пространстве плоскостей-экранов). Разумеется,
может найтись такое криволинейное
двумерное многообразие, с помощью которого будет возможно добиться еще меньших
значений перечисленных критериев. Способы построения таких оптимальных многообразий и составляют основу нашего изложения.
В своем рассмотрении мы почти полностью ограничиваемся
двумерным случаем, как наиболее естественным для визуализации. Понятно, что
метод главных компонент позволяет построить трех-, четырех- и более факторные
модели, и, вообще, выбрать k главных компонент, использование которых в качестве
факторов обеспечивало бы необходимую точность описания данных. Тогда можно
сказать, что набор данных является эффективно k-мерным. Разумеется, наиболее интересны случаи, когда k существенно
меньше размерности пространства.
Некоторые выводы
Итак, мы качественно рассмотрели основную модель
многомерного статистического анализа данных – многомерное нормальное
распределение. В качестве оптимальных факторов, описывающих данные, в этой
модели выступают линейные комбинации признаков, задающие в пространстве
направления, вдоль которых дисперсия данных максимальна. Простота и изученность
такой модели связана как раз с её линейностью.
Можно сказать, что
нормальное распределение возникает всякий раз, когда создается статистическая
модель линейной системы. Поскольку
точные науки хорошо умеют справляться почти исключительно только с такими
простыми системами, то легко понять популярность нормального распределения в
физике, химии, биологии и так далее.
Как мы уже упоминали,
традиционным первым шагом в статистическом исследовании является оценка
математического ожидания и общей дисперсии для набора данных (в многомерном
случае – ковариационной матрицы, то есть по сути m дисперсий, где m – размерность
пространства). Эти величины являются достаточными статистиками нормального
распределения, то есть первым и традиционным шагом является представление набора
данных в виде простейшей линейной модели.
Если облако точек является
явно более сложным, например, имеет более одной точки сгущения, то его в первом
приближении можно моделировать пространственным наложением нескольких
нормальных выборок, для каждой из которых определена своя ковариационная
матрица и набор главных компонент. Если считать каждую из точек данных вершиной
своей нормальной «шапочки» распределения, то в результате такого наложения
возникает самый простой из непараметрических способов оценивания плотности
распределения генеральной совокупности.
С другой стороны, за
исключением модельных тестовых примеров, практически все реальные данные по
своей структуре оказываются весьма далеки от нормальных выборок, точно так же
как реальные физические системы почти всегда отнюдь не линейны.
В связи с этим особый
интерес представляют принципиально нелинейные способы моделирования и
визуализации данных, позволяющие построить эффективную технологию анализа
реальных таблиц данных.
Для начала в традициях
построения физических моделей природы рассмотрим возможные полумеры – малые
отклонения от линейного (нормального) случая.
1.2.5. Квазилинейные подходы
Выше мы уже упоминали, что моделирование (и визуализация)
данных с помощью линейных факторов является оптимальными лишь в случае близкого
к нормальной выборке облака точек данных. Если это не так, то есть нормальное
распределение никаким образом не может являться моделью данных, то для их моделирования
необходимо, как минимум, прояснить следующие моменты:
1. Выбрать критерий оптимальности, согласно которому будет
решаться задача построения моделирующего многообразия, и, собственно,
разработать способ построения этого многообразия.
2. Определить способ, с помощью которого точки данных из
исходного пространства будут переноситься на моделирующее многообразие. В
случае, если оптимальным многообразием является плоскость, такой проблемы нет –
наиболее естественным является ортогональное проецирование на плоскость.
" На самом деле и в этом
случае возникает ряд вопросов. В многомерном пространстве для вложенной
двумерной плоскости вектор нормали определен неоднозначно. Под ортогональным
проектированием обычно понимают проектирование в ближайшую точку плоскости,
однако для различных метрик такая точка, вообще говоря, может быть разной. В
частности, для обычной евклидовой и взвешенной евклидовой метрики ортогональные
проекции не совпадают. "
Смесь гауссовых компонент
Во-первых, один из очевидных способов обобщения линейных
моделей является представление общего распределения данных в виде взвешенной
суммы нормальных распределений, должным образом «сшитых» друг с другом, для
каждого из которых оптимальным моделирующим многообразием является линейное многообразие,
натянутое на несколько собственных векторов ковариационной матрицы
соответствующей нормальной компоненты смеси. Из отдельных кусков этих
плоскостей можно так или иначе сшить главную поверхность. Согласно критерию
оптимальности определяется состав набора нормальных компонент, коэффициенты
смеси, условия сшивки и т.д.
Очевидно, что чем больше нормальных компонент будет в
смеси, тем, с одной стороны, более криволинейной будет полученная в результате
сшивки поверхность. В предельном случае каждая точка данных может
использоваться как представитель своей нормальной компоненты (этот случай может
быть использован для непараметрических оценок плотности распределения). С
другой стороны, чем меньше точек определяют каждую нормальную компоненту, тем
менее ясен смысл вычисления собственных векторов соответствующей ковариационной
матрицы (в упомянутом предельном случае вообще ни о каких собственных векторах
речи не идет, соответствующие дисперсии либо полагаются равными заданной
величине «окна», либо применяются какие-либо варианты их оценки по положению
соседей).
В целом, подход, основанный на построении оптимального
многообразия с использованием модели смеси нормальных распределений, является
весьма вычислительно трудоемким. Кроме собственно решения проблемы построения
моделирующего многообразия необходимо решать задачу разбиения множества данных
на компактные подмножества, то есть решать, фактически, задачу кластерного
анализа, и, таким образом, становится понятно желание подойти к проблеме с иных
позиций.
Сглаженные квазилинейные
развертки данных
После того, как построена первая из главных компонент, у
нас, после применения операции проектирования каждой из точек на прямую,
соответствующую главной компоненте, появляется возможность сопоставить каждой
из точек данных определенное число – координату. Достаточно только произвольным
образом выбрать на прямой начало отсчета, см. рис. 10). Поскольку после
проецирования все точки лежат на одной прямой, то они оказываются
упорядоченными. В результате появляется возможность последовательно соединить
соседние точки данных отрезками и в результате получить одномерную развертку
данных, то есть такое одномерное многообразие, которое проходит через все точки
данных согласно выбранному способу упорядочивания данных.
" Существуют другие способы
упорядочивания точек данных таким образом, чтобы близкие в пространстве точки
оказались соседями на полученной развертке. Например, можно упомянуть метод адаптивной развертки, в котором
точки данных упорядочиваются согласно следующему алгоритму [19].
1.
Найти точку данных xi, для которой суммарное расстояние до остальных объектов максимально,
то есть dS(xi)= max. Это будет первая точка в развертке.
2.
Из еще не вошедших в развертку точек найти такую точку xj, для которой выполняется
условие  , где z – точка, полученная на
предыдущем шаге,
, где z – точка, полученная на
предыдущем шаге, ![]() – суммарное расстояние
от объекта xj до его M ближайших соседей, M и b – параметры метода. Эта
точка будет следующей в развертке.
– суммарное расстояние
от объекта xj до его M ближайших соседей, M и b – параметры метода. Эта
точка будет следующей в развертке.
3.
Шаг 2 повторяется до тех пор, пока все точки не окажутся в развертке.
Пример
применения метода адаптивной развертки см. на рис. 11. "
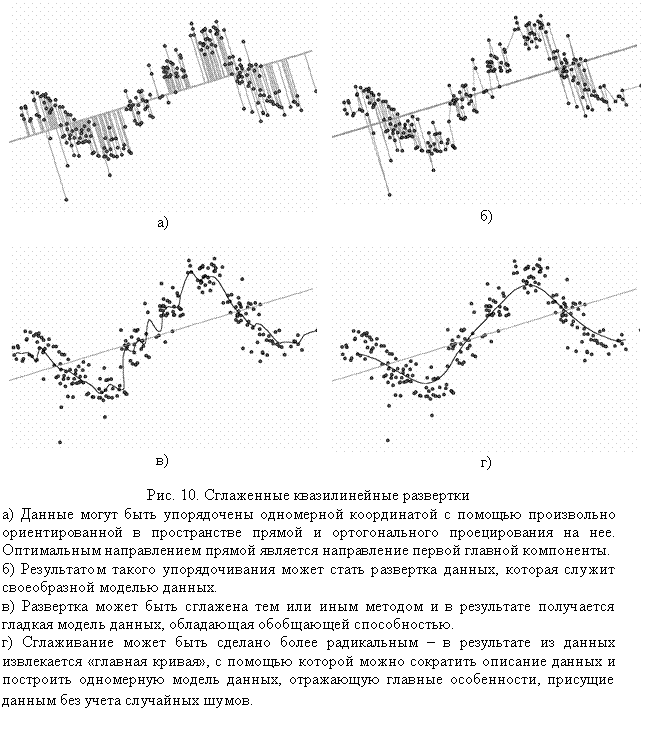
Преимуществами такой развертки является то,
что исчезает проблема проецирования данных на полученное многообразие – точки
данных и так ему принадлежат. Кроме того, что данные оказываются
упорядоченными, из них можно извлечь информацию, например, о взаимном
расстоянии между соседними точками, направлении отрезков, соединяющих соседние
точки и которую можно графически отобразить с помощью разного рода диаграмм.
Однако, практическая полезность такого многообразия, как
модели данных, находится под вопросом. Во-первых, как уже отмечено, данные
могут быть заданы с допуском или погрешностью, и, соответственно, их положение
в пространстве определено не точно. Во-вторых, данные вообще могут содержать
пробелы – и тогда многообразие оказывается не определено. И, наконец, самым
большим недостатком является то, что такая модель данных не отслеживает общей тенденции (или закона), содержащегося в данных, кроме той, что заключена в способе
упорядочивания. Если данные «зашумлены» – а именно это характерно для реальных
наборов данных – то полученная ломанная отслеживает все случайные флуктуации –
таким образом, длина описания данных в такой модели не сокращается – для
задания положения вершин ломанной необходимо то же количество информация, что и
для описания всех координат точек данных.

Вообще, возникшая ситуация достаточно характерна. При
построении модели данных исследователю всегда приходится искать компромисс
между точностью представления данных и обобщающей способностью модели.
Увеличивая число задаваемых параметров модели, можно добиться сколь угодно
малой погрешности описания тех данных, которые были использованы для построения
модели. Однако, цель создания такой модели –
обобщение некоторого «опыта», накопленного в данных; при этом не
достигается. Это значит, что для любого объекта, который не был использован при
создании модели, погрешность его описания может быть весьма велика. Более
подробно мы остановимся на этом моменте в следующем разделе.
Тем не менее, можно улучшить обобщающую способность
полученной выше развертки, если сгладить полученную ломанную. Некоторые
конкретные варианты сглаживания рассмотрены во второй главе. Здесь нам важнее
подчеркнуть, что при использовании сглаживания возникает, как минимум, один
параметр, который является регулятором типа «точность-общность». Чем более
точной по отношению к описанию исходных данных мы делаем нашу модель – тем
большее количество параметров необходимо задавать для описания модели.
Предельный случай – полученные выше развертки. С другой стороны, увеличивая общность модели,
мы снижаем количество необходимых для описания модели параметров за счет
снижения точности описания исходных данных и получаем в пределе линейное подпространство,
натянутое на главные компоненты.
Итак, сглаженные линейные развертки, которые могут быть
положены в основу построения квазилинейных одномерных моделей данных, возникают
в результате конкуренции двух факторов – стремления описать исходные данные как
можно точнее и сделать модель более гладкой, сокращая при этом длину описания модели.
Квазилинейность подхода заключается в том, что он существенным образом
использует построенную линейную модель данных, и надстраивается над ней.
Квазилинейные модели могут быть построены и в двумерном
случае, надстраиваясь над плоскостью двух первых главных компонент. Тогда
каждая точка после проектирования на плоскость получает две координаты и
данные, естественно, уже не будут упорядочены в прямом смысле слова. Тем не
менее, взяв за основу двумерные координаты каждой из точек можно построить
сглаженную двумерную поверхность, форма которой будет как-то отражать
отклонения распределения данных от нормального.
1.2.6. Существенно
нелинейные случаи
Роль линейных методов в статистике весьма велика.
Существует общий рецепт – если линейный метод работает хорошо и решает
поставленные задачи – то его и следует использовать, даже если нет
статистически оправданных посылок для его применения. Однако, часто ситуация
бывает обратной, и тогда задача исследователя
– описывать данные «так, как они есть», без использования дополнительных
предположений о характере их распределения.
Исследователь должен, прежде всего, сформулировать критерий
оптимальности, которому должна удовлетворять модель данных. Такой критерий
должен обладать следующими свойствами:
1. Он должен быть компромиссным по отношению к конкуренции
между точностью описания и обобщающей способностью модели. По всей видимости,
критерий должен содержать параметры, позволяющие в зависимости от условий
задачи увеличивать то или другое свойство.
2. Желательно, чтобы критерий был таким, чтобы для
нормального распределения данных для него наилучшей моделью являлись линейные
многообразия, натянутые на главные компоненты. Это позволит сравнивать преимущества
такого моделирования по сравнению с традиционными методами.
Задачу построения модели данных можно сформулировать как
задачу аппроксимации многомерного набора точек данных более или менее гладкими
поверхностями, вложенными в многомерное пространство.
" Аппроксимацией в самом общем определении называется метод,
заключающийся в замене сложных объектов другими, более простыми. В этом смысле
сложное многомерное множество точек данных заменяется более простым и
регулярным объектом – многообразием или сеткой, для описания которой требуется
меньше информации. "
1.2.7. Нейросетевые модели
данных
В нашем изложении при построении аппроксимирующих
поверхностей мы предпочитаем говорить на «языке геометрии». То есть, по
возможности, явно представлять себе размещение аппроксимирующей поверхности в
многомерном пространстве. Однако, стоит отметить, что вполне возможно вести
изложение и на другом языке – например, нейросетевом, который стал в последние
десятилетия очень популярен. В наши задачи не входит изложение методов
нейросетевого анализа данных, однако, подчеркнем, что как результат работы
нейросети так или иначе может быть представлен геометрически, так и практически
любой из алгоритмов, приведенных в этой книге может быть естественным образом
«переведен» на нейросетевой язык. Так, например, способ построения карт
Кохонена, о которых речь пойдет ниже, традиционно излагается с помощью описания
соответствующей нейросетевой архитектуры. Задача снижения размерности данных
может быть описана как с помощью наглядных образов криволинейных поверхностей,
вложенных в многомерное пространство, так и с помощью описания такой нейросети,
в которой число входов равно размерности пространства, а количество выходов
равно размерности моделирующего многообразия.
" Более интересно рассмотреть
нейросеть «с узким горлом» (см. рис. 12). В ней число выходов равно число
входов, но сеть содержит внутренний слой с небольшим числом нейронов. Сеть
обучается на воспроизведение входов – то есть ответ нейросети считается
правильным, когда значения сигналов на каждом выходе совпадает со значением на
соответствующем ему входе. Если удается обучить такую нейросеть, то она
способна решать задачу сокращения размерности – и тогда сигнал необходимо
снимать с нейронов «горла» сети, и задачу проецирования данных, не вошедших в
задачник, в пространство меньшей размерности. "
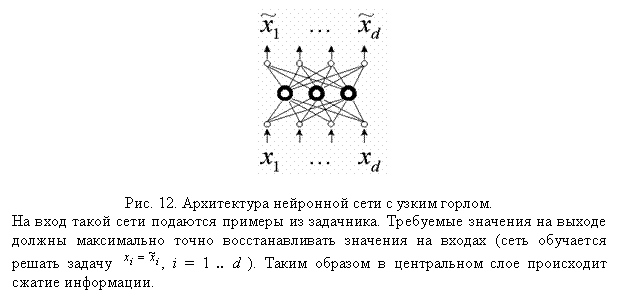
Тем не менее, возможность перевода алгоритмов на
нейросетвую основу является очень ценной, поскольку в случае реального
применения алгоритмов на практике, нейросетевой подход позволяет получать
высокоэффективные параллельные архитектуры при аппаратной реализации алгоритмов
в устройствах.
Для нас будут важны некоторые понятия, характерные для
описания функционирования нейросетевых моделей. Так, для обучения нейросетей
важен поиск компромисса между величиной ошибки
обучения и ошибки обобщения. Под
первой подразумевается средняя погрешность воспроизведения сетью тех данных, которые
были использованы для ее обучения (например, процент случаев с правильным
распознанием класса для исходного набора данных). Как правило, если обучающая
выборка не является противоречивой, с помощью увеличения числа нейронов и
синаптических связей можно добиться сколь угодно малой ошибки обучения. Для
оценки ошибки обобщения необходимо иметь тестирующую выборку, то есть набор
«проверочных заданий», которые не были использованы для обучения. Как правило,
если исходных данных достаточно много, то часть из них может быть удалена из
процесса обучения и использоваться для оценки обобщающей способности нейросети.
В нейросетевых подходах регулятором типа
«точность-общность» является число нейронов и синаптических связей сети, число
слоев нейросети или время обучения (для циклических сетей), вид нелинейности
характеристической функции. Как правило, исследователь экспериментирует с этими
параметрами с целью добиться приемлемых результатов. Успех применения
нейросетей и своеобразный «нейробум», с ними связанный, с одной стороны, вызван
тем обстоятельством, что нейросетевые архитектуры позволяют получать
информационные модели и «хорошими» аппроксимационными свойствами – а именно, в
отличие от давно известных интерполяционных формул, нейросети с хорошей
точностью описываю данные в местах их скоплений и гладко интерполируют их в
местах их разрежения, а, с другой стороны, с высокоэффективными приемами
обучения нейросетей (такими, как вычисление градиентов с помощью обратного
функционирования и т.д.)
1.2.8. Физикалистские игры с данными. Преобразования
пространства данных.
Вообще говоря, смысл расстояния между двумя точками в
пространстве признаков весьма условен. За редкими исключениями, расстояние не
имеет никакого физического смысла, кроме меры различения объектов. С одной стороны,
это создает проблему выбора подходящей метрики, с другой – манипулируя этим выбором,
исследователь имеет возможность добиваться определенных «эффектов» над
представлением облака данных с целью подчеркнуть те или иные особенности их
структуры.
Начнем с того, что предобработка данных может
рассматриваться на языке изменения метрики пространства признаков. Линейные
преобразования значений признаков (например, нормировка на среднеквадратичное
отклонение, интервал) приводят к различным линейным метрикам. Часто
оказывается, что набор значений отдельных признаков полезно подвергнуть
нелинейному преобразованию (например, если значения признака отличаются на
порядки, то логично применить какой-либо вариант логарифмического преобразования).
Удачно выбранное преобразование пространства признаков
вообще может нелинейную задачу распознавания образов свести к линейной
(например, в случае распределения данных, расположенных вдоль поверхностей
концентрических сфер). Разумеется, крайне трудно «угадать» подходящее преобразование
без предварительного анализа структуры данных, но если такой «разведочный»
анализ укажет на существование определенных зависимостей в пространстве
признаков, то задачи классификации, снижения размерности могут быть существенно
упрощены.
Рассмотрим некоторые идеи, возникающие в этом направлении.
Все они могут быть реализованы как варианты в процессе предобработки данных
перед их визуализацией.
Гравитирующие данные
Если дать волю фантазии, то на преобразование пространства признаков,
которое, в конечном итоге, приводит к тому, что меняются расстояния между объектами
в пространстве, можно посмотреть с иных позиций, и предположить, что эти
расстояния меняются не из-за выбора метрики, а вследствие того, что сами точки
данных обладают подвижностью. Разумеется, нет нужды интерпретировать конкретные
траектории движения точек данных, интерес представляет только их новое
расположение, в котором будет достигаться минимум какого-либо функционала от
координат положений точек.
Первое, что приходит в голову – это определенным образом
задать закон взаимодействия частиц-точек друг с другом, указав, например,
какой-либо центрально-симметричный (хотя и не обязательно) потенциал
взаимодействия. Точки данных в таком подходе могут как отталкиваться, так и
притягиваться друг к другу, им можно приписывать различную «массу», то есть
некоторые точки могут считаться «весомее» других. Взаимодействие между
частицами может быть дальнодействующим (по типу гравитации) или иметь
определенный радиус (по типу ядерных сил). Частицы могут взаимодействовать
выборочно (например, если заданно разбиение множества точек на подмножества, то
точка может взаимодействовать сильнее с точками, принадлежащими ее же классу). В любом случае критерий оптимальности
конфигурации точек – величина энергии их взаимодействия, то есть после каждого
перемещения частиц суммарная энергия их взаимодействия должна становиться
меньше.
Рассмотрим, например, облако точек, гравитирующих в
многомерном пространстве признаков. Энергия их взаимодействия равна нулю в
пределе бесконечного разнесения точек и становится отрицательной и бесконечной
в случае, если все точки собрались
вместе. Таким образом, облако точек будет стремиться «коллапсировать».
Разумеется, если все точки окажутся собранными вместе, то будет потеряна всякая
информация о первоначальной структуре данных, поэтому параллельно с гравитацией
необходимо ввести эффект, приводящий к «разбеганию» точек друг от друга. Таким
образом, мы получаем своеобразную «Вселенную данных», в которой конкурируют два
процесса – с одной стороны, каждая их точек данных стремится притянуться к
близлежащим точкам – и это приводит к собиранию данных в «сгустки» - кластеры,
а с другой – происходит «расширение Вселенной». Такая конкуренция приводит в
результате к тому, что данные
автоматически собираются в компактные, отделенные друг от друга в пространстве
группировки, но при этом сохраняется информация о первоначальной структуре этих
группировок. Скорости конкурирующих процессов должны быть определенным образом
подобраны, чтобы, например, средняя плотность данных оставалась постоянной.
Конкретные варианты реализации предложенных идей приведены
в разделе 2.1.7.
Далее, можно устроить так, чтобы данные взаимодействовали
не друг с другом, а с многообразием, определенным образом вложенном в
пространство признаков. Таким образом, если мы, например, разместим среди
данных двумерную поверхность, то с помощью такой процедуры можно заставить
точку данных перемещаться к точке поверхности до тех пор, пока она не окажется
в непосредственной близости от многообразия.
И, наконец, может оказаться так, что более интересным будет
задать для точек потенциал отталкивания, а параллельно запускать процесс
«сжимания» Вселенной данных. Если скорости этих процессов будут подогнаны для
сохранения средней плотности, то в результате точки данных более или менее
равномерно заполнят доступный им вначале объем пространства.
Нелинейные преобразования пространства признаков.
Изложенная выше идея может быть рассматриваться в несколько
ином виде. Так мы можем задаваться целью некоторым регулярным способом
равномерно распределить данные в
исходном доступном им объеме пространства так, чтобы соседние данные оставались
соседними. Для этой цели необходимо тем или иным образом оценить плотность
данных (например, любым из непараметрических способов) и в тех областях, где
эта плотность высока «сжать координатную сетку» пространства, а где, наоборот,
данные расположены редко, «растянуть» координатные линии (см. рис.13)
а) б) в) Рис. 13. Преобразования
двумерного пространства признаков. а)
исходное распределение точек данных б)
координатная сетка для метрики, в которой данные распределены более
равномертно в)
координатная сетка для метрики, в которой подчеркнута кластерная структура
данных



В результате, данные нанесенные на
новую координатную сетку будут расположены почти равномерно (за исключением,
может быть, граничных областей).
Этот же тип преобразования можно применить
в обратном направлении, и тогда области с плотным размещением данных окажутся
еще более плотными, и наоборот. Таким образом, мы получаем своеобразный
регулятор «контрастности» кластерной структуры данных, «поворачивая» этот
регулятор в ту или иную сторону, мы можем или подчеркнуть кластерное разбиение
данных, либо, наоборот, размывать его. Соответствующие математические выкладки
приведены в разделе 2.1.5.
Существуют преобразования пространства
признаков, для которых критерием оптимальности является максимум суммы
квадратов коэффициентов линейной корреляции для некоторой группы признаков.
Такое преобразование может применяться в двух случаях:
1. При использовании номинальных и
порядковых шкал числовые метки шкалы, присваиваемые тем или иным признакам,
могут быть выбраны с большой степенью произвола, поскольку смысловую роль
играет не величина интервала между значениями меток, а только их порядок
следования. Таким образом, любое монотонное преобразование оставляет этот
порядок неизменным. Выбор функции преобразования часто осуществляется таким
образом, чтобы конечные наборы числовых меток обеспечивали максимальную степень
линейной зависимости между выбранными
признаками. Процедуры такого типа называются оцифровкой и предназначены для приведения признаков всех типов к
единой непрерывной количественной шкале.
2. Даже для непрерывных количественных
шкал признаков можно попробовать задаться определенным семейством
преобразований шкалы признака и оценить параметры семейства такие, чтобы
признаки после преобразования зависели друг от друга максимально линейно. Это,
как уже указывалось, может привести к существенному упрощению задач
распознавания образов и классификации.
Локальные статистики
В связи с темой нашего изложения можно
упомянуть относительно новый подход к анализу многомерных данных, связанный с
построением так называемых локальных статистик.
В основе этого подхода лежит идея о том, что преобразование пространства признаков
можно построить таким образом, чтобы удовлетворить определенному критерию
оптимальности не для всего набора данных, а лишь для его единственной точки.
Таким образом в методах, связанных с построением локальных статистик
рассматривается набор данных «с точки зрения» одного из объектов.
Как правило, удобно поместить начало
координат в ту точку, где находится этот «базовый» объект. После этого можно,
например, анализировать диаграммы распределения расстояний от точек данных до
начала координат. Из вида этих диаграмм, например, можно увидеть, принадлежит
ли точка данных крайним областям облака данных или находится внутри нее (см.
рис. 14)
Если множество данных изначально
разбито на классы, то таким образом можно представить себе как точки того или
иного класса расположены относительно «базовой» точки (рис. 14)
Приведенные
на рис. 14 диаграммы построены, исходя из предположения, что в обоих вариантах
выбора базовой точки, расстояние от нее до остальных измеряется с помощью одной
и той же евклидовой метрики. Однако, можно построить для каждой из выбранных
точек данных свою «локальную» метрику, удовлетворяющую определенному критерию.
В разных задачах этот критерий выбирается по-разному.
В задачах построения классифицирующих разделяющих
поверхностей можно поставить следующим образом: найти такое преобразование
метрики, в котором отношение суммы расстояний от базового объекта до объектов
своего же класса к сумме расстояний до объектов других классов минимально.
" Пусть xk координаты
выбранного в качестве базового объекта, wk – множество объектов его класса, dk(xk,xi) –
расстояние от xk до xi, измеренное в метрике,
построенной для «базового объекта» xk.
Тогда
упомянутый критерий выглядит следующим образом:  "
"
В результате применения такого подхода получается N локальных метрик (N – число объектов). В каждой из них можно построить
классифицирующую разделяющую поверхность (или, более общо, свое
классифицирующее правило), и получить коллектив
решающих правил (N классификаторов, каждый из которых производит
распознавание образов с точки зрения одного объекта) и применять к этому
коллективу соответствующие методы (например, различные варианты «голосования»).
В случае анализа структуры многомерных
данных можно, например, выбрать в качестве локальной метрику Махаланобиса. В
результате с точки зрения любой «базовой» точки распределение данных будет
выглядеть нормальным и изотропным (то есть данные будут расположены внутри
многомерного шара с радиусом, равным дисперсии, которая будет равна единице во
всех направлениях).
Следует отметить, что после того, как
для каждой точки данных построена некоторая локальная метрика, возникает
проблема измерения расстояния между объектами, поскольку расстояние, измеренное
в локальной метрике одного объекта не будет совпадать с расстоянием, измеренным
в локальной метрике другого объекта (будут нарушаться условия независимости
расстояния от направления измерения – от 1-го объекта ко 2-ому или наоборот, а
также возможно нарушение неравенства треугольника). Для преодоления этой
трудности на основе исходных N локальных
метрик конструируется некоторая новая, общая для всех то чек данных метрика, в
которой в некоторой степени будут присущи свойства локальных. Различные
варианты построения таких обобщенных метрик рассмотрены в разделе 2.1.8.
а) б) в) г) д) Рис. 14. Построение
локальных статистик а) исходное распределение данных; точки исходно разделены на два
почти неперекрывающихся класса; квадратом и треугольником выделены точки
на границе и в центре облака соответственно; б),в) диаграммы распределения расстояний от
выделенных объектов до всех остальных (по оси x
–
расстояния до объектов, по y – их количество); на
первой диаграмме можно выделить две вершины диаграммы, соответствующие
двум точкам сгущения в облаке данных; г),д) диаграммы распределения расстояний от
выделенных объектов до объектов двух классов; из первой диаграммы видно,
что с помощью статистики объекта, помеченного квадратом, можно построить
разделяющее классы правило, а для треугольника – нет.




