МЕТОДЫ
СИНТЕТИЧЕСКОГО КАРТОГРАФИРОВАНИЯ ТЕРРИТОРИИ
(НА ПРИМЕРЕ ЭКОЛОГО-ИНФОРМАЦИОННОЙ СИСТЕМЫ "VOLGABAS")
В.К.Шитиков,
Г.С.Розенберг, Н.В.Костина
Количественные методы
экологии и гидробиологии
(Сборник
научных трудов, посвященный памяти А.И. Баканова).
Отв. ред. чл.-корр. РАН Г.С. Розенберг. – Тольятти:
СамНЦ РАН, 2005. – С. 167-227.
Институт
экологии Волжского бассейна РАН,
stok1@list.ru
- *** -
Геоинформатика глазами
экологов (вместо введения)
1. Формальная постановка задачи визуализации данных
2. Представление пространственной информации в
эколого-информационных системах
3. Анализ характера распределения показателей и алгоритмы их
перевода в нормированные шкалы
4. Методы классификации и редукции данных
5. Введение в "индексологию"; алгоритмы получения
комплексных показателей
6. Моделирование причинно-следственных связей
7. Примеры синтетического картографирования Волжского бассейна с
"правильными словами и веселенькими картинками"
8. Примеры картограмм по Самарской области
Геоинформатика глазами экологов
(вместо введения)
“Карты бывают разные:
игральные, топографические, медицинские…”
[Гражданская защита, 1997, № 3 , стр. 54]
Однозначного
ответа на вопрос что есть карта? , по-видимому,
нет: так Дж. Эндрюс собрал и проанализировал 321 различных определений карты,
используя публикации с 1649 по 1996 гг. Как определяет толковый словарь [1],
"Карта (map, chart) –
математически определенное, уменьшенное, генерализованное изображение поверхности
Земли, другого небесного тела или космического пространства, показывающее
расположенные или спроецированные на них объекты в принятой системе условных
знаков". Напомним, что генерализация (generalization) –
формализованный отбор, сглаживание или упрощение характеристик объекта с целью
выделения главных его типических черт. Генерализация осуществляется всегда на
основе некоторых фильтров и формальных критериев, субъективно принятых автором
для решения поставленных им задач.
Более
"взвешенный" взгляд на карту содержится в рабочем определении,
принятом 10-й ассамблеей Международной картографической ассоциации: знаковое
изображение географической реальности, отображающее отдельные
ее особенности или характеристики как результат творческого авторского
отбора и предназначенное для использования в тех случаях, когда
пространственные отношения имеют первостепенное значение. В этом
определении зафиксированы следующие важные моменты:
1.
знаковость
(символьность) картографического изображения;
2.
отображение
географической реальности;
3.
субъективный
творческий характер этого отображения;
4.
приоритет
пространственных отношений.
В то же время, как
указывает А.М.Берлянт [2], в этом определении отсутствуют упоминания о том, что
карта:
1.
построена по особому математическому закону;
2.
может
отображать не только географическую реальность, но и абстракции, мысленные и
даже фиктивные объекты;
3.
способна представлять не только пространственные, но и динамические ситуации,
их изменения во времени.
Дальнейшая
абстракция от реальности приводит нас к мысли, что пространственные отношения
не обязательно должны иметь географический смысл, а евклидовы
координаты x-y являются лишь одними из многих возможных осей
математического многомерного пространства признаков. Живой пример "неправильных"
карт – подробно описываемые ниже самоорганизующиеся карты Т.Кохонена,
визуализирующие степень близости произвольных объектов.
Тезис о
"математической определенности" географических карт, возник из
целенаправленного стремления авторов [1,3] объединить понятия прикладной картографии
и геоинформатики. Поскольку четкого определения геоинформатики нет,
будем понимать под ней совокупность компьютерных и телекоммуникационных
технологий обработки данных для решения задач анализа геосистем.
В сближении
понятий картографии и геоинформатики много подводных камней.
Прежде всего, в очень разном стиле и нацеленности карты и геоинформационной
модели. Например, картограф (создавая карту как нематематическую модель
действительности) отобразит рельеф изучаемой местности одним из известных
способов: изолиниями, тональной отмывкой и иногда - цифрами в "командных
точках". А в геоинформатике та же карта представляется цифровой,
структурно-цифровой, структурно-каркасной, структурно-лингвистической моделями.
Обе модели имеют несколько разный смысл. Картограф, используя язык карты, стремится прежде всего визуализировать информацию, чтобы
сделать ее читаемой, не задумываясь над некой ее "математической
определенностью". Основным же продуктом геоинформационной технологии
является генерирование новой информации путем алгоритмически целенаправленного
"пережевывания" и "переваривания" имеющегося массива
данных.
Более 35 лет назад
началась разработка геоинформационных систем (ГИС). Быстро пройдя этапы
создания упрощенных картосхем и грубых имитаций бумажных атласов, современные
программно-аппаратные комплексы последовательно обобщили достижения
традиционного картосоставления и научились изготавливать произведения самого
высокого качества. Электронные карты, полученные с помощью таких продуктов
ГИС-индустрии, как Arcview, MapInfo и т.д., стали точнее обычных ручных в
геометрическом отношении, более разнообразны по цветовому, штриховому,
полутоновому оформлению, по яркому дизайну. Одновременно с усвоением
традиционного опыта геоинформационное картографирование постепенно вышло на
новый уровень. Сегодня картографы-геоинформатики все чаще задумываются о
создании панорамных художественных произведений, в
корне отличающихся от традиционных карт и атласов. Например, трехмерное
цифровое моделирование позволяет строить объемные изображения, а анимации
придают картам так необходимый им динамический аспект.
Но с какой целью
затрачиваются столь существенные усилия на реализацию функций чисто “офисного”
характера, обеспечивающих максимальный сервис визуализации, географическую
эстетику и координатную точность? Разве лишь только для того, чтобы
воспроизвести топографическую карту с помощью компьютерной системы взамен
существующей традиционной топокарты? Оказать впечатление на неподготовленного
зрителя грандиозными эффектами визуализации, напоминающими голливудские
фильмы-блокбастеры? Полагаем, что вовсе нет. Более привлекательна, например,
перспектива построения оценочных и прогнозных пространственных моделей за счет систематизации,
определенной группировки, преобразования больших массивов многомерной
информации, чтобы вести контроль геоситуации и решать оптимизационные задачи,
иногда вообще не прибегая к визуализации.
Геоинформатика
поражает и покоряет немыслимыми массивами данных, которыми она играючи
оперирует, однозначностью и воспроизводимостью результата. Однако генерирование
новой информации, свойственное ГИС-технологиям, содержательно интересно только
тогда, когда кто-то извне, представитель иной сферы знания или же целая другая
наука вложили в уста геоинформатики содержательное понимание определенной
задачи. В этом смысле геоинформатика тесно смыкается с экоинформатикой.
Картографический
метод для изучения пространственного распределения земной биосферы на видовом и
ценотическом уровнях стал использоваться задолго до того, как была сформирована
экология как наука и осознана миссия человечества как одного из важнейших
условий устойчивого развития планеты. Первые попытки оценить и представить в
визуально обозримой форме биоразнообразие Земли предпринимались в XVIII–XIX
веках на схемах ботанико-географического и зоогеографического разделения
поверхности планеты по степени своеобразия флоры и фауны. Среди них выделяется
исследование Д.Скоу (1823, цит по [4]), который, используя метод
статистического изучения видового состава растительного покрова, предложенный
Р.Броуном и А.Гумбольдтом (1807),. одним из первых выделил естественные
флористические подразделения на основе количественных характеристик флоры и с
учетом природных особенностей территории.
Постепенно
выделилась самостоятельная область науки, которая стала заниматься
пространственным анализом природных систем - ландшафтная экология. Термин
“ландшафтная экология” был, видимо, впервые употреблен К.Троллем (Troll, 1939,
цит. по [5]) и стал использоваться для обозначения науки, изучающей
экологический эффект мозаичности природных систем в широком диапазоне
пространственных масштабов (Turner 1989). Фактически, ландшафтная экология
сфокусирована на изучении трех основных характеристик природных комплексов
(Forman, Godron, 1986):
1.
структуры - пространственных связей между отдельными
экосистемами или элементами (в простейшем понимании – пространственного
распределения энергии, вещества и видов);
2.
функций - взаимодействия пространственных элементов, т.е.
потоков энергии, вещества и видов между компонентами экосистем;
3.
изменений
структуры и функций экологической мозаики во времени.
Кратко говоря,
ландшафтная экология рассматривает развитие и динамику пространственной неоднородности и ее влияние на экологические процессы, а
также управление пространственной неоднородностью (Risser et al., 1984).
Углублением
понятий о пространственной структуре экосистем явилось формулировка концепций
экологической ниши. Д.Хатчинсон (Hutchinson, 1957) определяет фундаментальную
нишу как область в абстрактном многомерном гиперпространстве, осями которого
являются не только географические координаты местообитаний, но и переменные
условий среды. Это - по сути первый опыт, когда изначально трехмерное
географическое пространство с фиксированным смыслом осей x-y
трансформировалось в многомерное, причем появилась возможность сформировать
различные низкоразмерные отображения (т.е. частные карты экосистем), оси
которых имели смысл , например, различных факторов
среды ( топоклины встали в один ряд с экоклинами, хроноклинами
и проч.).
Большой вклад в
развитие картографирования биосферных элементов внесен под влиянием системной
парадигмы Б. Сочавы. Разработанный им (1979) структурно-динамический подход
позволил отражать на картах не только пространственную, но и
пространственно-временную организацию экосистем. На основе концепции эпитаксонов,
где растительные сообщества комплексно диагностируются по динамическому
состоянию, степени устойчивости и "сукцессионной продвинутости",
построен, например, мелкомасштабный атлас растительности Европейской части
СССР.
Картографическое
обеспечение такой сложной и многоплановой проблемы, как структурный анализ
экосистем, должно создаваться на основе комплексного подхода. Картографический
банк данных территории формируется из карт разной тематики и степени
пространственно-временной интеграции информации, разного масштаба и назначения.
В него, кроме карт видового или ценотического
биоразнообразия, включаются также карты землепользования и землевладений с
выделением особо охраняемых природных территорий, карты экологически важных
параметров среды (климата, рельефа, литологии и др.), сведения о рекреационной
нагрузке, заболеваемости населения и проч. При этом сколько-нибудь осмысленный
анализ информации невозможен без привлечения статистических и мониторинговых
данных о реальной и прогнозируемой антропогенной нагрузке: сведений об объеме
и местах локализации атмосферных выбросов, вывоза твердых
отходов, сброса сточных вод, характере и условиях распространения поллютантов в
природной среде, результатов натурных химико-аналитических измерений.
Традиционным
методом комплексного анализа в геоинформатике является построение синтетических
оценочных картограмм. Терминологически этот процесс трактуется следующим
образом[1]:
"Синтетическая
карта (synthetic map) – карта, дающее
интегральное изображение объекта или явления в единых синтетических
показателях. Чаще всего, С. к. отражают типологическое районирование
территории по комплексу показателей (напр., ландшафтное, климатическое
районирование, деление территории по условиям жизни населения и т. п.).
Картограмма (choropleth
map, cartogram, chorogram, chorisogram) - 1. карта, показывающая
распределение относительных показателей (плотность, интенсивность какого-либо
явления, удельные величины и т. п.) по определенным территориальным единицам,
чаще всего – административным; - 2. один из способов картографического
изображения, применяемый для показа относительных статистических данных
путем заполнения контуров территориального деления (обычно, административных
единиц) цветовыми заливками (solid) разного тона, штриховками
(cross-hatch line pattern) разной плотности в соответствии с принятыми
интервальными шкалами. Средства автоматизации позволяют строить К. в т.
н. непрерывных, или безинтервальных шкалах (choropleth
maps without class intervals, continuous-tone cartogram), когда плотность
ставится в точное соответствие величине картографируемого показателя."
Синтетические показатели
создаются обычно путем обобщения (в простейшем случае – суммирования)
достаточно большого числа исходных показателей, численно распределенных по
координатной сети анализируемой территории [6-7]. Сколько-нибудь серьезный
математический аппарат, необходимый для формирования комплексных оценочных
карт, в ГИСах стандартной комплектации отсутствует: так пакет Arcview 3.1
располагает лишь простейшими оверлейными операциями по совмещению
пространственно-распределенных тематических слоев (одновременное открытие с
наложением). Типовых ГИС, предназначенных для целенаправленной ситуационной
обработки фактографической и картографической информации об экологическом
состоянии природно-хозяйственных территорий, в настоящее время не существует
[8].
Сегодня мы находимся
на этапе, когда программное обеспечение ГИС производится уже достаточно широко,
но все еще не является предметом потребления для широкого круга пользователей
персональных компьютеров. Другие продукты информационных технологий (текстовые
редакторы и электронные таблицы, бухгалтерские и торговые системы) стали
обыденными предметами потребления. ГИС-индустрия в целом до такого положения
вещей не дошла. Она все еще занимается адаптацией приложений к потребностям
индивидуальных заказчиков (в первую очередь - традиционных географов). Но эта ситуация уже в корне изменяется, потому что начинают
появляться разработки малых и средних производителей ГИС с простым, зачастую
тривиальным ГИС-оформлением, которые решают задачи конечных пользователей
пространственных данных - экологов, управленцев, пользователей систем учета и
анализа, а не специфические задачи географов. При этом возникающие
решения занимают пустующие ниши на рынке универсальных ГИС, которые не
вписываются в инструментарий и/или доступную массовому пользователю общую
стоимость изделия (напомним, что цена традиционной ГИС колеблется от 1,5 до 5
тыс. долларов США).
Безусловно, ряд
ортодоксальных экспертов геоинформатики относится к таким
"облегченным" программам крайне настороженно, но если крупные поставщики
ГИС не выработают своих собственных аналогов подобных пакетов, то в будущем их
наверняка ждет вытеснение с рынка. Суть заключается в том, что пользователям
нравится простой продукт с интуитивным интерфейсом, который делает именно то,
что от него хотят. При этом такое решение часто стоит на порядки дешевле своих
"старших братьев" и обладает открытой архитектурой, что позволяет его
наращивать и развивать в контексте возникающих в процессе эксплуатации новых
требований.
Существующий
диссонанс между элитарным характером геоинформационных технологий и реальными
потребностями специалистов-аналитиков является одним из тормозов в развитии
общих концепций синтетического картографирования в области практической
экологии и рационального природопользования. До настоящего времени не
существует типовой унифицированной система - рубрикатора базы данных исходных индивидуальных признаков и результирующих
эколого-экономических критериев (критериев “оптимальности”), т.е. комплексных
показателей количественного и качественного состояния наземных территорий и
акваторий, характеризующих их уязвимость или экологическое благополучие. Не
разработан непротиворечивый и математически корректный формализм
"свертки" исходного пространства признаков в отображаемые синтетические
показатели ("индексы"). В связи с этим, несмотря на существование
ряда региональных атласов территорий, нет общепринятой методологии оценочного
или прогнозного картографирования эколого-экономических комплексов, основанной
на системном синтетическом подходе.
Литература
1.
Баранов Ю.Б., Берлянт А.М., Капралов Е.Г., и др. Геоинформатика. Толковый словарь основных терминов. -
М.: ГИС-Ассоциация, 1999.-204 с.
2.
Берлянт А.М.
Виртуальные геоизображения. М., 2001
3.
Тикунов В.С.
Моделирование в картографии. М.: Изд-во МГУ, 1997. 408 с.
4.
Лебедева Н.В., Криволуцкий Д.А., Пузаченко Ю.Г. География и мониторинг биоразнообразия. М.:Изд-во
НУМЦ, 2002. 432 с.
5.
Савельев А.А. Моделирование
пространственной структуры растительного покрова (геоинформационный подход. Казань: Изд-во Казанского
гос. Университета. 2004. 244 с.
6.
Новиков М.А. Оценочное
эколого-рыбохозяйственное районирование морских акваторий // Водные ресурсы.
2004, т.31, № 2, с.199-208.
7.
Исаченко А.Г. К
методике прикладных ландшафтных исследований // Изв. ВГО. 1972. Т. 104. № 6. С.
417-429.
8.
Жуков
В.Т., Новаковский БА., Чумаченко А.И. Компьютерное геоэкологическое
картографирование. М.: Науч. мир. 1999. 128 с.
1.
Формальная постановка задачи визуализации данных
В этом разделе мы
приводим обзор тех методов, которые в настоящее время используются для
визуального представления сразу всей структуры многомерного набора данных [1].
Для визуализации могут быть использованы 1-, 2- и 3-мерные пространства
отображений, но мы в своем рассмотрении практически целиком ограничимся
способом визуализации с помощью 2-мерных поверхностей, поскольку именно в таком
виде человек воспринимает геометрические структуры наиболее
естественно и отношения между объектами выглядят наиболее наглядно.
Под визуализацией
данных мы понимаем такой способ представления многомерного
распределения данных на двумерной плоскости, при котором, по крайней мере,
качественно отражены основные закономерности, присущие исходному распределению
– его кластерная структура, топологические особенности, внутренние зависимости
между признаками, информация о расположении данных в исходном пространстве
и т.д.
В качестве основных
применений методов визуализации можно указать следующие:
а) наглядное представление геометрической метафоры данных;
б) лаконичное описание внутренних закономерностей, заключенных в наборе данных;
в) сжатие информации, заключенной в данных;
г) восстановление пробелов в данных;
д) решение задач прогноза и построения регрессионных зависимостей между
признаками.
Один из способов
целенаправленного проецирования в пространства малой размерности (в зарубежной
литературе – projecting pursuit) заключается в следующем: найти такое
отображение U (способ проецирования) из исходного пространства на двумерную
плоскость, которое бы оптимизировало заданный критерий качества Q – некоторый
функционал от координат точек данных до и после процедуры проецирования: Q(U,X).
Здесь под X понимается весь набор многомерных данных, а Q зависит
от параметров отображения.
Например, если
каждой точке многопараметрических данных можно было бы приписать две координаты
(например, с использованием квазилинейной модели), то это позволяет построить в
пространстве данных гладкое многообразие, которое обладает свойством обобщать
заключенную в данных информацию и служить для лаконичного описания, сжатия
информации или для восстановления пробелов в данных. Тогда проецирование данных
в пространство меньшей размерности заключается в настройке процедуры построения
моделирующей двумерной поверхности, вложенной в многомерное пространство
признаков.
Можно выделить
различные варианты решения задачи проецирования:
1.1.
Процедура ортогонального проецирования (метод главных компонент)
В этом случае вид
отображения U известен заранее и является линейным отображением на
плоскость.
Допустим, что
облако объектов “похоже” на выборку из генеральной совокупности, подчиненной
закону нормального распределения (уточнению понятия “похоже” посвящена
литература по проверке статистических гипотез, например [2], здесь мы не будем
вдаваться в тонкости этой серьезной науки). Попробуем дать описание
распределения точек данных в пространстве, которое имеют одну точку сгущения (унимодальную
плотность) в точке среднего арифметического значений всех признаков. Чем
ближе к этой точке, тем выше плотность распределения объектов. Более 60% всех
объектов находятся в области, представляющей собой эллипсоид рассеяния,
центрированный в точке сгущения с осями, равными собственным значениям
ковариационной матрицы (см. рис. 1).
Проведем прямую
через центр сгущения, ориентированную вдоль наибольшей вытянутости (дисперсии)
облака данных (см. рис. 1а). Это направление совпадает с направлением
наибольшей по длине оси эллипсоида рассеяния. Назовем такую
прямую первой из главных компонент и отметим, что для нее средний
квадрат расстояния до точек данных минимален.
|
|
|
|
Рис. 1а. Двумерное
нормальное распределение точек. |
Рис. 1б. Искажения, возникающие при
проецировании. |
Первая из главных компонент
соответствует самой существенной долей извлеченной из набора данных информации,
причем тем более существенной, чем длиннее наибольшая из осей эллипсоида
рассеяния по сравнению с остальными. Значения координат вектора, задающего
направление первой из главных компонент, являются количественными мерами
значимости признаков (чем меньше значение соответствующей координаты, тем менее
значим и информативен признак). Уравнение главной компоненты позволяет
приближенно восстановить значения всех признаков, если известно значение только
одного из них.
Если точность
такого моделирования данных оказывается недостаточной, то определяется
направление второй из главных компонент. Из векторов, соответствующих каждой
точке данных вычтем вектор ортогональной проекции точки на первую главную
компоненту. Назовем новый полученный набор векторов множеством первых
остатков. Построим в этом множестве первую главную компоненту. Ее
направление окажется направлением второй главной компоненты для исходного
множества. Это будет прямая, проходящая через центр распределения,
перпендикулярно к первой из главных компонент, совпадающая с направлением
второй из главных полуосей эллипсоида рассеяния.
На полученные два
вектора можно натянуть плоскость первых двух главных компонент. Среди
всех плоскостей эта плоскость обладает свойством минимума суммы квадратов
расстояний от нее до точек данных. С помощью нее можно а) построить
двухфакторную модель данных; б) восстановить значения признаков объекта, если
известны значения двух признаков; в) простым образом визуализировать
многомерные данные, спроецировав каждую точку данных ортогонально на плоскость
первых двух главных компонент.
Итак, наиболее
приемлемым способом визуализировать набор точек данных, чье распределение
“похоже” на выборку из нормальной генеральной совокупности, является
ортогональное проецирование на плоскость первых двух главных компонент.
Плоскость проектирования является, по сути плоским двумерным “экраном”,
расположенным в пространстве таким образом, чтобы обеспечить “картинку” данных
с наименьшими искажениями.
Такая проекция будет
оптимальна (среди всех ортогональных проекций на разные двумерные экраны) в
трех отношениях:
1) Минимальна сумма квадратов расстояний до точек данных, то есть экран
расположен максимально близко по отношению к облаку точек.
2) Минимальна сумма искажений расстояний между всеми парами точек из облака
данных после проецирования точек на плоскость.
3) Минимальна сумма искажений расстояний между всеми точками данных и их “центром тяжести”, а также сумма искажений углов
между векторами, соединяющими точки и “центр тяжести”.
Кроме минимизации
расстояния от точек данных до их проекций в качестве оптимизируемого
функционала могут быть использованы и другие проекционные индексы, например,
максимизация энтропии конечного двумерного распределения данных [3].
1.2.
Многомерное шкалирование
Если считается,
что вид отображения U заранее неизвестен, тогда в качестве
оптимизируемого критерия минимизируют функционал, описывающий “меру искажения” структуры
данных. Одним из самых популярных является функционал, являющийся аналогом
стресса в многомерном шкалировании и описывающий меру искажения взаимных
расстояний между точками в исходном и результирующем пространстве отображения.
Многомерное шкалирование
используют в том случае, когда исходная информация изначально представлена не в
виде таблицы типа “объект-признак”, а в виде квадратной таблицы удаленностей
объектов друг от друга. На пересечении i-ой строки и j-ого
столбца в такой таблице стоит оценка расстояний от i-го до j-го
объекта. Таким образом, изначально каждому объекту не сопоставляется никакой
координаты в многомерном пространстве и представить
такую информацию в виде геометрической метафоры затруднительно.
Задача многомерного
шкалирования заключается в том, чтобы сконструировать распределение данных
в пространстве двух шкал таким образом, чтобы расстояния между объектами
соответствовали заданным в исходной матрице удаленностей. Возникающие
координатные оси могут быть интерпретированы как некоторые неявные факторы,
значения которых определяют различия объектов между собой. Если попытаться
сопоставить каждому объекту пару координат, то в результате мы получим способ
визуализации данных.
В литературе [4]
описаны различные алгоритмы многомерного шкалирования, хотя сами вычислительные
процедуры этих алгоритмов практически не отличаются. В частности, в метрическом
нелинейном методе размерность пространства задается изначально и с помощью
градиентных методов оптимизируется функционал качества, называемый стрессом
и описывающий меру искажения матрицы удаленностей.
Аналогично
традиционному факторному анализу, в многомерном шкалировании существует
неоднозначность выбора координат, связанная с тем, что координатную систему в
полученном пространстве можно произвольным образом повернуть – расстояния между
объектами при этом не изменяются. Как правило, поворот осуществляют таким
образом, чтобы либо полученные координатные оси имели максимально наглядную
интерпретацию, либо значения определенных признаков оказались максимально
скоррелированы.
1.3.
Снижение размерности с учетом нелинейности данных
Возникает
естественный вопрос – а как обстоит дело с наборами данных, которые не могут
считаться выборками из генеральной совокупности с нормальным распределением?
Разумеется, почти всегда можно найти такое криволинейное двумерное
отображение U, с помощью которого будет возможно добиться еще лучших
значений критериев оптимизации Q. Но существует общий рецепт: если
линейный метод работает хорошо и решает поставленные задачи, то его и следует
использовать, даже если нет статистически оправданных посылок для его
применения.
Однако, часто
ситуация требует описывать данные “так, как они есть”, без использования
дополнительных предположений о характере их распределения. Тогда задачу
проецирования данных можно сформулировать как задачу наилучшей аппроксимации
многомерного набора точек данных более или менее гладкими нелинейными
поверхностями, вложенными в это пространство. В этом смысле сложное многомерное
множество точек данных заменяется более простым и регулярным объектом –
многообразием или сеткой, для описания которой требуется меньше информации.
Задача снижения
размерности данных может быть описана как с помощью наглядных образов различных
криволинейных поверхностей, вложенных в многомерное пространство, так и с
помощью описания такой нейросети, в которой число входов равно размерности
пространства, а количество выходов равно размерности моделирующего
многообразия. В наши задачи не входит подробное изложение методов нейросетевого
анализа данных, который стал в последние десятилетия очень популярен и читатель
легко удовлетворит свое любопытство [5-7].
Рассмотрим
автоассоциативную сеть нейросеть “с узким горлом” (см. рис. 2). В ней число
выходов равно число входов, но сеть содержит внутренний слой с небольшим числом
нейронов. Сеть обучается на воспроизведение входов – то есть ответ нейросети
считается правильным, когда значения сигналов на каждом выходе совпадает со
значением на соответствующем ему входе (![]() ). Если удается обучить такую нейросеть, то она способна
решать задачу сокращения размерности – и тогда сигнал необходимо снимать с
нейронов “горла” сети.
). Если удается обучить такую нейросеть, то она способна
решать задачу сокращения размерности – и тогда сигнал необходимо снимать с
нейронов “горла” сети.
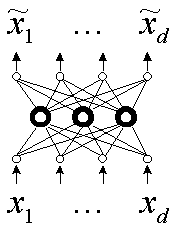
Рис. 2.
Архитектура автоассоциативной нейронной сети с узким горлом.
Трехслойная
автоассоциативная сеть сначала линейно преобразует входные данные в меньшую
размерность промежуточного слоя, а затем снова линейно разворачивает их в
выходном слое. Можно показать, что такая сеть на самом деле реализует
стандартный алгоритм анализа главных компонент. Для того,
чтобы выполнить нелинейное понижение размерности, нужно использовать пятислойную
сеть, средний слой которой служит для уменьшения размерности, а соседние с ним
слои, отделяющие его от входного и выходного слоев, выполняют нелинейные
преобразования. Если из пятислойной обученной автоассоциативной сети удалить
два последних слоя, то получается сеть для проецирования, с помощью которой
генерируется версия входных данных, преобразованных в пространство, размерность
которого равна числу нейронов третьего оставшегося слоя.
Итак, в основе
методов целенаправленного проецирования и многомерного шкалирования лежит идея
оптимизации некоторого функционала, который зависит от начального положения
точек в пространстве и конечного расположения точек на двумерной плоскости.
Выбирая различные виды функционалов, можно строить различные проекции данных,
на которых будут подчеркнуты те или иные их особенности. В целом такой подход
является достаточно прозрачным и ясным, но при его практическом использовании
возникают определенные трудности.
Во-первых, задача
оптимизации нелинейной функции является трудной сама по себе. В большинстве
методов используются, как правило, градиентные процедуры, требующие больших
вычислительных затрат, которые растут пропорционально квадрату от числа точек
данных.
Во-вторых,
оказывается, что выразительная картина многомерного распределения данных,
изображенная на двумерной картинке еще не решает всех вопросов, которые может
поставить себе исследователь. Заманчива идея наносить на двумерную карту не
только сами точки данных, но и разнообразную информацию, сопутствующую данным:
например, отображать так или иначе положение точек в
исходном пространстве, плотности различных подмножеств, другие непрерывно
распределенные величины, заданные в исходном пространстве признаков. Все это
подталкивает к мысли использовать как можно полнее тот “фон”, на который
наносятся данные, а также вид самих точек данных для отображение различной количественной и атрибутивной
информации.
Наконец, после
того, как данные нанесены на двумерную плоскость, хотелось бы, чтобы появилась
возможность расположить на двумерной плоскости те данные, которые не
участвовали в настройке отображения. Это позволило бы, с одной стороны,
использовать полученную картину для построения различного рода экспертных
систем и решать задачи распознавания образов, с другой – использовать ее для
восстановления данных с пробелами.
Таким образом,
можно подойти к естественному обобщению понятия карты, как объекта,
который представляет из себя ограниченное двумерное
нелинейное многообразие, вложенное в многомерное пространство данных таким образом,
чтобы служить моделью данных.
Простой пример
карты данных – плоскость первых двух главных компонент. Как мы уже упоминали,
среди всех двумерных плоскостей, вложенных в пространство, она служит
оптимальным экраном, на котором можно отобразить основные закономерности,
присущие данным. В качестве другой, еще более простой (но не оптимальной) карты
можно использовать любую координатную плоскость любых двух информативных
переменных, в том числе, и пространственных, если географические координаты
являются приоритетными для анализа данных.
Обобщением способа
представлять данные с помощью метода главных компонент будет случай, когда
карта может иметь любую нелинейную форму, не используя в процессе построения
карты никаких гипотез о распределении данных. Детальному описанию процедур
создания и интерпретации гибких карт посвящена прекрасная монография [8].
1.4.
Топологические изображения и самоорганизующиеся карты
До сих пор мы
представляли карту как ординацию изучаемых объектов и/или их свойств в системе
двух ортогональных метрических осей. Другим способом картографирования является
формирование в общем случае неметрического топологического изображения в
виде гипотетической “эластичной сети”, с узлами которой соотнесено
континуальное (непрерывное) изменение свойств анализируемых объектов. Узлы
(нейроны) такой сети соединены между собой связями и образуют проекционный
экран. Обычно используются два варианта соединения узлов – в прямоугольную и
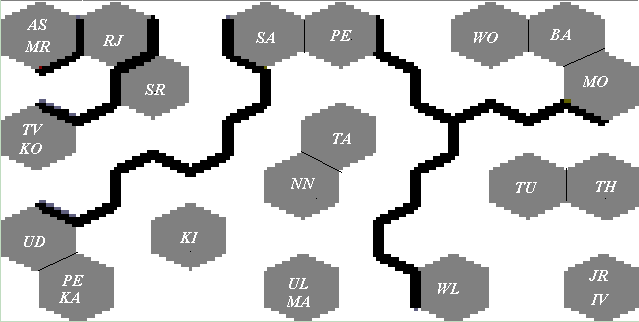
гексагональную сетку (см. рис. 1) – отличие состоит в том, что в прямоугольной
сетке каждый узел соединен с 4-мя соседними узлами, а в гексагональной – с 6-ю
ближайшими соседями.
|
а) |
|
Рис. 3. Два варианта расположения узлов сетки
топографического изображения
а) прямоугольная сетка, б) гексагональная сетка
Формирование
топографического изображения может быть реализовано с использованием нейронных
сетей особого типа – так называемых самоорганизующиеся структур, обучаемых
"без учителя" по аналогии с известными принципами функционирования
нервных клеток [9]. В этих сетях на слой нейронов, составляющих
проекционный экран, подается входной образ, состоящий из векторов исходных
данных,, и сигналы возбуждения распространяются по всему слою согласно
принципам классических прямопоточных (feedforward) сетей, то есть для каждого
нейрона рассчитывается взвешенная сумма его входов, к которой затем применяется
передаточная функция нейрона, в результате чего получается его выходное
значение. Процесс обучения заключается в подстраивании весов синапсов,
которое осуществляется только на основании информации, доступной в нейроне, то
есть его состояния и уже имеющихся весовых коэффициентов.
Т.Кохонен [10-11]
предложил модификацию алгоритма соревновательного обучения Хебба, в
результате чего пропорциональный вклад стали получать не только
нейроны-победители, но и ближайшие их соседи, расположенные в окрестности R.
Вследствие этого положение нейрона в выходном слое стало коррелировать с
положением прототипов в многомерном пространстве входов сети, т.е. близким
нейронам стали соответствовать близкие значения входов X.
"Проекционный экран" в процессе обучения приобрел свойства
упорядоченной структуры, в которой величины синапсов нейронов плавно меняются
вдоль двух измерений, имитируя двумерную сетку координат.
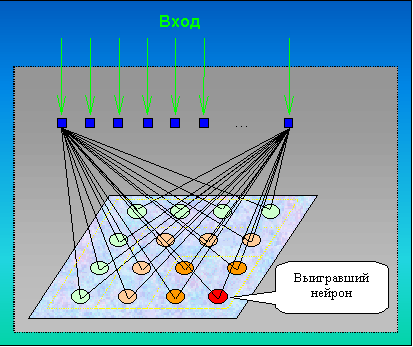
Такой способ
отображения получил название самоорганизующихся карт (SOM –
Self-Organizing Maps или SOFM – Self-Organizing Feature Maps), которые сразу
превратились в мощный аналитический инструмент, объединяющий в себе две
основные парадигмы анализа – кластеризациию и проецирование, т.е. визуализацию
многомерных данных на плоскости.
Самоорганизующиеся
карты, относящиеся к топографическим отображениям, аппроксимируют изменения
свойств анализируемых объектов, поскольку воспроизводят на выходе нейронной
сети топологический порядок и определенную степень регулярности (сходства)
метрически близких векторов исходных данных. Понятие топографии в SOM
определено на нескольких уровнях:
1.
Сохранение топологии.
В наиболее общем смысле подобие между структурой исходных данных и картой
определяется структурой соседства в множестве точек
данных и нейронов (узлов), то есть топологией. В этом случае топография
означает сохранение топологии и эквивалентной непрерывности отображения входного
набора данных на выходной.
2.
Сохранение порядка.
Более строгим значением такого подобия является сохранение порядка расстояний
между парами точек данных и соответствующими парами нейронов, на которые эти
точки отображают Это означает, что большие расстояния
переходят в большие монотонным образом, возможно, без соблюдения какой-то
фиксированной пропорциональности.
3.
Сохранение
метрических свойств. Еще более
строгое понимание подобия основано на прямом вычислении метрических (то есть
выраженных численно) расстояний между парами точек и соответствующими парами
нейронов. В таком смысле топография означает сохранение метрических отношений.
Рассматривая
отображение, построенное в результате применения алгоритма обучения SOM, как ординационное,
можно выделить несколько существенных отличий. Традиционные ординации либо
требуют задания заранее известных осей и шкал на них (например, георгафические
координаты или факториальные градиенты среды), либо используют только одну ось
(например, различные методы построения дендрограмм). Использование заранее
определенных шкал возможно только при надлежащей калибровке исходных данных,
что не всегда возможно. Использование дендрограмм не позволяет отобразить всю
структуру “взаимоотношений” классов в силу своей
дихотомичности (Савельев, 2004).
Таким образом,
нейронные сети Кохонена и их обобщения являются в настоящее время практически
единственным средством, позволяющим (в силу адаптивности и самоорганизации
нейронной сети, не требующей предварительной калибровки данных, устойчивости к
шумам и искажениям) выполнить ординацию и выявить структуру объектов с учетом
всей совокупности данных.
Литература
1.
Зиновьев А.Ю., Питенко А.А., Россиев А.А. Проектирование многомерных данных на двумерную сетку.
// 2-я Всероссийская научно-техническая конференция “Нейроинформатика-2000”.
Ч.1. М.: МИФИ.– 2000. С.80-88.
2.
Кендалл М., Стюарт А.
Статистические выводы и связи.- М.: Наука, 1973.-900 с.
3.
Айвазян С.А., Бухштабер В.М., Енюков И. С., Мешалкин Л. Д. Прикладная статистика. Классификация и снижение
размерности.- М.: Финансы и статистика, 1989.-607 с.
4.
Терехина А.Ю. Анализ
данных методами многомерного шкалирования.- М.: Наука, 1986.-168 с.
5.
Горбань А.Н., Россиев Д.А.
Нейронные сети на персональном компьютере. Новосибирск: Наука (Сиб. отделение),
1996. 276 с.
6.
Ежов А.А., Шумский С.А.
Нейрокомпьютинг и его приложения в экономике и бизнесе. М.: Изд-во МИФИ, 1998.
7.
Шитиков В.К., Розенберг Г.С., Зинченко Т.Д. Количественная гидроэкология: методы системной
идентификации. Тольятти: ИЭВБ РАН, 2003. 463 с.
8.
Зиновьев А.Ю. Визуализация
многомерных данных.
9.
Блум Ф., Лейзерсон А., Хофстедтер Л. Мозг, разум и поведение, М., Мир, 1988.
10.
Кохонен Т.
Ассоциативные запоминающие устройства. – М.: Мир, 1982. – 383 с.
Kohonen T. Self-organization and Associative
Memory.Springer-Verlag:
2.
Представление пространственной информации в эколого-информационных
системах
Актуальность
проблемы и некоторые банальности
Природные
экологические системы в настоящее время испытывают на себе постоянно
возрастающие антропогенные воздействия, вызванные активной хозяйственной
деятельности человека с одновременным ростом его популяции. Увеличение
земельно-эксплуатируемых территорий ведет к разрушению природных структур. В
результате постоянного развития производства десятки и сотни тысяч химических
соединений создаются и используются человечеством, многие из которых (в том
числе токсичные и радиационные) попадают в биосферу, загрязняя ее. В связи с
этим, экологическая оценка состояния окружающей среды, изучение механизма
деятельности, структурных особенностей, анализ целостности и устойчивости
природных систем, прогнозирование их динамического развития, определение
возможной деградации экосистем и степени ухудшения качества жизни человека -
являются в настоящее время важнейшими задачами современной экологии.
Оценка
экологической обстановки и степени "уязвимости" биосферы является
непростой задачей, не имеющей принципиально однозначного решения. Термин качество
окружающей среды на практике имеет множество значений и трактуется
специалистами в различных областях по-разному и "трудно заставить
политиков, чиновников, ученых или простых людей прийти к единому мнению о том,
что он означает и как его измерить" (Элер, 1976).
Окружающая
среда человека состоит из четырех неразрывно взаимосвязанных
компонентов-подсистем:
1) собственно природная среда, имеющая свойство самоподдержания и саморегуляции
без корректирующего воздействия человека;
2) квазиприрода - модификации природной среды, в которых отсутствует внутреннее
самоподержание и которые требуют все больших энергетических затрат извне;
3) артеприрода - искусственная среда, созданная человеком и не имеющая аналогов
в естественной природе;
4) социальная среда.
Как
считает Н.Ф.Реймерс [1], все факторы из рассматриваемых сред тесно связаны
между собой и составляют объективные и субъективные стороны качества среды
жизни, которые должны быть учтены при экологической оценке состояния изучаемой
территории. В связи с этим, число показателей, которые могут быть использованы
для оценки экологического состояния, измеряется сотнями. Обработка такого
массива данных, его анализ, выявление "значимых" или
"несущественных" показателей весьма затруднительны без использования
совокупности компьютерных и телекоммуникационных технологий.
В
территориальных органах природоохранного мониторинга, учебных заведениях,
отраслевых институтах и специализированных краеведческих организациях в течение
ряда десятилетий накопился богатый фактографический материал по различным
аспектам исследований в области экономики, естествознания и медицины региона. В
подавляющем большинстве случаев этот материал никак серьезно не обрабатывается
и хранится в виде полузабытой "бумажной субстанции". Не исключено,
что собранная статистическими методами (в период обязательной отчетности
Госкомстату СССР), эта информация оказывается зашумлена и даже тенденциозна, а
ее пространственная привязка нередко оказывается весьма размытой. Тем не менее,
при разумном подходе к ее обработке и интерпретации, эти данные становятся не
только важным, но и определяющим звеном информационной модели территории. Во
всяком случае, вывод о необходимости проведения комплекса дорогостоящих
дистанционных исследований разумно сделать лишь после обобщения всего комплекса
уже имеющейся эколого-экономической информации.
Будем
понимать под региональной эколого-информационной системой реализованную
с помощью технических средств динамическую информационную модель территории,
отражающую пространственно-временную структуру, состояние и взаимосвязи между
отдельными элементами моделируемой экосистемы. Объектом анализа
экологического состояния может быть как отдельная
административно-территориальная единица (город, область, край, республика), так
и любая выделенная формальным или неформальным путем часть земной поверхности
(бассейн реки, природно-климатическая зона и т.д.). Необходимыми является два
условия:
1. наличие географической карты, на которой
изучаемая территория отображалась бы целиком;
2. наличие количественных показателей, имеющих
пространственно-распределенный характер и пригодных для ввода в базу данных.
Концептуальные "кирпичики" ЭИС и способы их реализации
Чтобы
не прибегать к надоевшим абстракциям, рассмотрим конкретную реализацию
территориальной базы экологических и экономических данных, разрабатываемой на
протяжении последних десятилетий в Институте экологии Волжского бассейна РАН
[2-5]. Описываемая ЭИС явилась одним из первых опытов комплексного анализа
пространственно распределенной информации и объединяет в себе следующую иерархию баз, образно интерпретируемую как
"экологическая матрешка":
1. комплексную базу данных, охватывающую
территорию 24 областей и автономных республик Волжского бассейна (более 90%
территории);
2. локальные базы по
территориям Самарской, Ульяновской, Саратовской и других областей;
3. частные базы данных, описывающие либо
отдельные регионы (например, г. Тольятти и прилегающую территорию
Ставропольского района), либо специализированные ресурсно-тематические блоки
(например, динамику гидрологических характеристик Куйбышевского водохранилища).
Естественно,
что при создании такого ансамбля баз данных ключевое место было уделено
процессам агрегирования информации в ходе ее прохождения от максимально
детализованных баз нижнего уровня к комплексным базам высшего уровня.
На
сегодняшний день одной из самых трудно решаемых проблем при разработке
интеллектуальных приложений, подобных ЭИС, является формализация предметной
области в виде N-мерной информационной модели. По определению,
любая модель ограничена, т.к. отбрасываются незначительные детали
и выделяется суть. Именно тут и проявляется первая из проблем – оценить,
что важно для решения поставленной задачи, а что нет? Выражаясь казенным
языком, необходимо разработать рубрикатор (список, тезаурус) тех данных, которые
подлежат загрузке в базу. Для решения этой проблемы мы не прибегали к
длительным раздумьям и воспользовались приведенной выше щедрой рекомендацией
Н.Ф.Реймерса "использовать все, что хоть сколько-нибудь похоже на
информацию".
Пространственно
распределенная информация ЭИС "REGION-VOLGABAS" охватывала следующий
рубрикатор природных компонент:
1. климат территории Волжского бассейна
(особенности распределения температуры воздуха и количества осадков, а также
ветрового режима);
2. географо-геологическое описание
(орография, дочетвертичный и четвертичный периоды
развития региона, основные черты тектоники) и геохимическая обстановка;
3. почвы и ландшафты Волжского бассейна,
наличие особо охраняемых природных территорий;
4. лесные ресурсы и распределение
естественной растительности;
5. животный мир Волжского бассейна (видовое
распределение и фаунистические комплексы наземных позвоночных и птиц);
6. население (демографическая ситуация в
Волжском бассейне и степень урбанизации территории);
7. гидрология и гидрохимическое качество
вод р. Волги и ее водохранилищ;
8. гидробиоценозы и их компоненты
(фитопланктон, зообентос, водяные клещи, инфузории, микроскопические водные
грибы, рыбные запасы бассейна Волги);
9. оценки качества воды и степени эвтрофикации
Волжских водохранилищ по видам-биоиндикаторам.
Обширные
рубрики накопленных данных детально описывали распределение по территории
техногенной нагрузки и антропогенных воздействий, в том числе:
1. загрязнение воздушного и водного
бассейна;
2. распределение отходов производства и
коммунального хозяйства (включая особо опасные вещества для состояния экосистем
и здоровья человека);
3. радиационная обстановка, места
техногенных аварий и природных катастроф;
4. транспортная и рекреационная нагрузка;
5. сельскохозяйственная нагрузка (включая
распределение по территории бассейна минеральных удобрений, распаханности
территории, животноводческой и пестицидной нагрузок).
Состояние
здоровья населения, как критерий оценки качества среды, в рамках ЭИС
"REGION-VOLGABAS" включало следующие параметры:
1. общая заболеваемость взрослого населения
(смертность, естественный прирост населения, оценки заболеваемости от
"экологически обусловленных" нозологий);
2. здоровье матери и ребенка (рождаемость,
смертность детей до года, общая заболеваемость детей, в том числе, от
"экологически обусловленных" нозологий);
3. инфекционные и паразитарные болезни,
частота злокачественных новообразований;
4. общее состояние системы здравоохранения.
Организация
данных в ЭИС пространственной ориентации в целом опирается не те же принципы,
что и в любой другой информационной системе, в первую очередь на некоторую
модель данных, в рамках которой представляется вся имеющаяся информация, как
пространственная, так и атрибутивная (описательная). Поэтому вторая из
проблем – понять, какова будет структура (состав полей) таблиц с данными и как
эти таблицы будут между собой взаимодействовать? Следует признать, что при разработки схемы базы данных мы
также не прибегали к мучительным мозговым атакам, поскольку структурно-логические
взаимодействия между информационными атрибутами подобных систем до неприличия
просты и не идут ни в какое сравнение, скажем, с тарифными планами небольшой
сотовой компании..
Модель базы данных, представленная на рис. 4, состоит
из двух типов таблиц: условно-постоянного назначения (рубрикаторы показателей и
списки операционно-территориальных единиц - участков, районов, городов,
областей и т.д.) и информационных таблиц (показатели в натуральных значениях, в
баллах, комплексные показатели), характеризующие каждую
операционно-территориальную единицу.
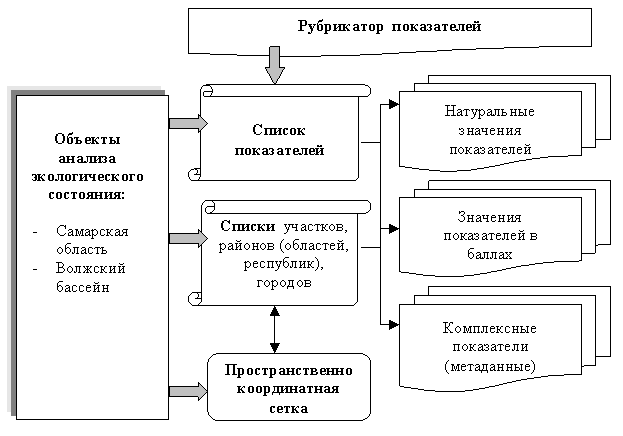
Рис. 4 Модель базы данных ЭИС типа "REGION"
Всего
ЭИС "REGION-VOLGABAS" содержала 509 предметных слоев карты, из
которых 85 составили обобщенные показатели. Для удобства пользовательского
интерфейса таблицы условно-постоянного назначения имели иерархический характер:
например, все показатели относились к одному из блоков, тем и подтем.
Развитие
визуальной интерпретации многомерных данных и ГИС-технологий связано, в
частности, с тем, что человеку с его ограниченным трехмерным пространственным
воображением сложно, а в большинстве случаев невозможно, анализировать и давать
обобщенные оценки многомерным объектам. Для реализации специфической проблемы
моделирования и прогноза пространственной структуры необходимо решение третьей
проблемы: выделение в рамках анализируемой картосхемы дискретных операционно-территориальных
единиц (ОТЕ) и геокодирование пространственных данных [6].
Каждая
ОТЕ является пространственным объектом, для которого предполагается однородность
имеющейся о нем атрибутивной информации с точки зрения изучаемого явления. В
традиционной растровой модели данных ГИС каждой ОТЕ соответствует ячейка
регулярной или нерегулярной сетки, которые покрывают полностью всю территорию
исследования; при этом размеры ячеек выбираются, исходя из характера
отображаемой информации и особенностей поставленной задачи. Теория и практика
геоинформатики предполагает также возможность реализации векторной модели
данных, когда цифровое представление данных связано с различными
геометрическими объектами (точкой, линией, дугой, замкнутым контуром и т.д.).
Однако, задавшись необходимой разрешающей способностью растровой сетки и
используя векторно-растровое преобразование, обе модели оказываются
информационно совместимыми.
На
основе выбранной ОТЕ происходит калибровка и настройка имеющейся атрибутивной
информации и приведение ее к единому образцу. В нашем случае на карте
территории выбирается пространственно-координатная сетка регулярного типа с такой
степенью масштабной детализации, которая удовлетворяет двум конкурирующим
условиям: минимальные потери информации и целостность зрительной интерпретации.
Для этого проводят на карте (n-1) горизонтальных и (m-1)
вертикальных параллельных линий, которые разделяют карту на m·n
прямоугольников или квадратов, именуемых в дальнейшем "участками". Участок
- это элементарный, далее не дробящийся объект привязки
пространственно-распределенной информации, т.е. постулируется: каждый
показатель в любой точке участка имеет одинаковое численное значение.
При
построении регулярной сетки учитываются следующие обстоятельства:
1. должно быть обеспечено удобство
координатной привязки, простота построения и охват всей территории, целостность
восприятия получаемых результатов;
2. увеличение количества участков должно
быть оправдано степенью детализации имеющихся пространственно-распределенных
показателей, их уровнем пространственной подробности;
3. слишком большое количество участков
приводит к лавинообразному увеличению размерностей матриц при дальнейшей
программной обработке, что приводит к непроизводительному расходу ресурсов
памяти, увеличению времени счета и т.д. и может не соответствовать мощности
имеющегося компьютера.
При
создании пространственно-координатной сетки территория Волжского бассейна была
разбита на 210 участков единичной площадью 6,5 тыс. км2,
территория Самарской области - на 287 участков единичной площадью 193 км2
и т.д.
Поскольку
настоящая методика создавалась в первую очередь для административно-территориальных
единиц, на карте изучаемой территории выделяются районы и города.
Район в общем смысле - связанное подмножество выделенных
участков, количество которых может быть произвольным (от 1 до m·n).
Однако не должно быть ни одного участка территории, не отнесенного ни к одному
из районов, как не должно быть участка, отнесенного к нескольким районам
одновременно. Выделение района как объекта информации определяется лишь
традицией представления статистической информации (например, заболеваемость
населения, отстрел животных, водоиспользование и т.д.). Для Волжского Бассейна
районами являются входящие в него области, автономные республики и прочие
административные единицы.
Город в общем смысле - специальным образом интерпретируемый
участок картосхемы, по которому имеются самостоятельные значения показателей.
Каждый город должен находится на территории какого-либо района. Выделение
городов связано с теми же обстоятельствами, что и выделение районов.
Наконец,
четвертой проблемой является геокодирование и пространственная
унификация данных.
Как
уже отмечалось, задача построения модели пространственной структуры экосистемы
является весьма сложной и требует совместного учета большого числа весьма
разнородных факторов. Сама эта разнородность имеет как тематическую, так и пространственную
природу. Пространственная разнородность информации выражается в том, что
статистические и описательные данные часто соотносятся с различными
пространственными объектами, отличающимся и по своей природе, и по масштабу,
что создает дополнительные трудности при совместной обработке и анализе
информации (Савельев, 2004).
Например,
численность популяции какого-либо вида в одних случаях может быть представлена
одним числом, отнесенным к искусственной пространственной единице (в частности,
административному району), что не позволяет делать достоверных выводов о ее
пространственной структуре. В других исходных материалах та же численность
может быть отнесена к выделенным на территории отдельным местообитаниям, в
которых вид встречается. Кроме того, информация о природных или
народно-хозяйственных объектах, как правило, известна не для всей территории, а
только для отдельных ее точек. Так, содержание загрязняющих веществ в почве
известно только в местах отбора проб; интенсивность движения транспорта известна
только на самих дорогах, хотя косвенно влияет (за счет передвижения населения)
на значительные территории.
Другая
проблема - различный масштаб представления информации. Так, при комплексном
региональном анализе приходится сопоставлять данные различного территориального
уровня - относящиеся ко всему региону в целом, к отдельным районам, к отдельным
водосборным бассейнам, к отдельным точечным описаниям. Размерность объектов,
которым соответствуют описательные данные, также может различаться - это могут
быть площадные, линейные или точечные объекты, или различные ячеистые
структуры. В тоже время, многие биосферные и диффузионные явления зависят не
только от состояния в данном конкретном месте, но и от значений этого
показателя на соседних (в широком смысле) участках территории. Для учета такого
влияния необходимо использование геостатистических методов, как правило, не
представленных в стандартных ГИС.
Очевидно,
что прежде чем проводить анализ или моделирование описанных выше
пространственно распределенных сущностей, вся разнородная информация, как о
зависимых, так и о независимых переменных должна быть тщательно оцифрована и
унифицирована по отношению к одним и тем же географическим координатам. Для
выполнения этой процедуры был разработан комплекс алгоритмов и программных
модулей эвристической, линейной и нелинейной интерполяции атрибутивных данных
по пространственным участкам (ОТЕ). После их реализации
пространственно-распределенные данные становятся активизированными. Поскольку в рассматриваемой ЭИС была принята единая растровая
модель данных, где ОТЕ соответствуют ячейкам регулярной прямоугольной сетки,
каждый показатель экосистемы Х (или фактор среды), в
унифицированном виде представлял собой переменную, определенную для каждого
участка области исследования:
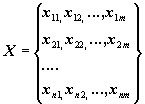 ,
,
причем
в представленной матрице активными являются только N значений внутри
контура территории, а (n× m - N) остаются неопределенными, т.е. на картограммах не
отображаются и в математическом моделировании не участвуют.
Для
текущей работы с базами данных разработано программное обеспечение, реализующее
традиционные в таких случаях функции:
1. многоаспектный поиск и формирование в
режиме диалога подмножества показателей по имеющимся рубрикационным полям;
2. графическое отображение на экране
дисплея картограммы пространственного распределения каждого показателя базы по
участкам территории;
3. получение расчетных таблиц оценки
структурных и модельных характеристик (например, составляющие техногенных и
биоэнергетических потоков);
4. получение новых (интегральных)
показателей путем линейной комбинации подмножества других показателей,
имеющихся в базе, либо по иным расчетным формулам;
5. математическая обработка показателей
базы с целью экологического районирования анализируемой территории, выявления
участков, подверженных наибольшему антропогенному воздействию, оценки
биотического и геохимического состояния отдельных природных комплексов.
Последние
пункты представленного перечня свидетельствуют о том, что основная задача
эколого-информационных систем - не только накапливать текущую или
ретроспективную информацию, но и формулировать стратегии управления
"качеством" окружающей среды. Для этого в составе программного
обеспечения "RЕGION-VOLGAВАS" была
разработана процедура генерации обобщенных критериев в виде линейной комбинации
исходных показателей, предварительно преобразованных в дискретную форму. С
целью математической обработки данных, хранящихся в ЭИС, кроме общепринятых
методов многомерного статистического анализа (регрессионный анализ, различные
алгоритмы обработки временных рядов, кластерный анализ и т.д.), использовались
алгоритмы построения прогнозирующих моделей методами самоорганизации
(эволюционное и нейросетевое моделирование, метод группового учета аргументов,
карты Кохонена). В качестве надстройки к библиотеке ("коллективу")
методов была разработана эвристическая процедура "модельного штурма",
реализующая синтез модели-гибрида из частных моделей-предикторов. Частичному
описанию концепций и компонентов программного обеспечения посвящены последующие
разделы.
Литература
1. Реймерс Н.Ф. Экология (теории, законы, правила, принципы и
гипотезы) - М.: Журнал "Россия Молодая", 1994 - 367 с.
2. Розенберг Г.С., Беспалый В.Г.,
Гайворон Т.Д. и др. База эколого-экономических
данных крупного региона (методическое пособие). – Тольятти: ИЭВБ АН СССР, 1991.
3. Розенберг Г.С.,
Краснощеков Г.П., Шитиков В.К. К
созданию пространственно-распределенной базы эколого-экономических данных
бассейна крупной реки (на примере Волжского бассейна) // Вопросы экологии и
охраны природы в лесостепной и степной зонах: Межвед. сб. науч. тр. – Самара: Изд-во "
Самарский университет" , 1995. С. 8-15.
4. Моисеенкова Т.А., Шитиков В.К. Принципы организации регионального банка эколого-экономической
информации // Моделирование процессов экологического развития (М., ВНИИСИ АН
СССР). 1989. № 7. С. 110-117.
5. Розенберг Г.С., Дунин Д.П. Базы экологических знаний: технология создания и
предварительные результаты // Изв. СамНЦ РАН. 1999. Т. 1. № 2. С. 186-192.
3.
Анализ характера распределения показателей и алгоритмы их перевода в
нормированные шкалы
Экологические и
экономические показатели, составляющие основу информационного обеспечения ЭИС
REGION, имеют следующие специфические особенности:
1) До сих пор не
выработан строгий и единый перечень количественно измеряемых параметров,
однозначно представляющих эмпирическую экологическую систему; и не установлен
исчерпывающий перечень операций, которые необходимо провести, чтобы оценить тот
или иной определяющий фактор. Поскольку существуют различные
формальные подходы к способам измерения продукции биоценозов,
экологического разнообразия, идентификации сукцессионных изменений,
устойчивости тренда экологической динамики, структурных сдвигов в видовом
составе и т.д., то одному и тому же теоретическому понятию, как правило,
соответствует несколько операциональных величин, отражающих различные точки
зрения.
2) Короткие ряды
наблюдений и далеко не всегда экспериментальный характер данных очень затрудняют
процесс регистрации показателей и нередко ставят под сомнение научную
значимость результатов их измерений. В силу колоссальной
пространственно-временной изменчивости биосферных объектов, нет никакой
уверенности в том, что имеющиеся выборки отражают реальные процессы. Очень
велика роль субъективного фактора: экологические величины формируются в ходе
определенной деятельности биологов и характеризуют каким-то образом эту
деятельность.
3) Показатели,
загружаемые в таблицы баз данных, представлены в самых разнообразных шкалах
измерений: номинальных, порядковых и метрических. Показатели, измеренные в
метрических шкалах, имеют самые разнообразные единицы измерения, масштаб, точки
отсчета и интервалы варьирования.
4) Эмпирические
ряды измерений подчиняются самым разнообразным законам распределений, весьма
далеким от теоретических нормального или равномерного.
Графики зависимостей часто имеют вид стохастических флуктуаций, приближающихся
к "белому шуму". Угрожающие масштабы принимает проблема идентификации
"выбросов", фильтрации аномальных и восстановления пропущенных
значений.
Аналогичные выводы
могут быть сделаны и в отношении других разделов базы данных:
медико-статистических показателей, описанию промышленного потенциала и
сельскохозяйственной продуктивности территориального комплекса. Поэтому
флуктуации субъективного порядка, возникающие по перечисленным причинам в
массивах входной информации, могут приводить к огромным отличиям получаемых
значений измеряемых величин от их действительных значений. В связи с этим,
решающее значение для получения адекватных результатов математического
моделирования является разработка развитой системы препроцессинга исходных
данных.
В статистической
обработке данных широко применяется нормировка – то есть линейное
преобразование всех значений признаков таким образом, чтобы значения признаков
попадали в сопоставимые по величине интервалы:
![]() ,
,
где: xij:
– j-ая координата i-го вектора, А и В
– некоторые заранее назначенные числа, которые назовем характерными
масштабами. Эти числа могут быть определены, исходя из статистических
характеристик распределения эмпирических выборок (нормирование по
статистикам), либо заданы по некоторым априорным соображениям (нормирование
по стандартам). В качестве "стандартов" могут выступать
фоновые или критические значения показателя, ПДК, наилучшие и наихудшие
"благоприятные" значения и прочие оценки [1-3], лексически связанные
с проблемой анализа критических или допустимых нагрузок. Понятийно эти оценки
легко воспринимаются, однако отсутствуют методы их корректного вычисления, а
существующие отдельные попытки экологического нормирования следует считать
субъективными.
В многомерном
облаке данных существует несколько масштабов нормирования по статистикам, когда
вариационный ряд каждого отобранного показателя преобразуется с использованием
выборочных статистических характеристик. Во-первых, это геометрический центр
многомерного облака точек данных ![]() (т.е.
среднее значения всех признаков), квадратный корень из общей дисперсии s ,
называемый среднеквадратичным отклонением и масштаб R, характеризующий
максимальный разброс в облаке данных
(т.е.
среднее значения всех признаков), квадратный корень из общей дисперсии s ,
называемый среднеквадратичным отклонением и масштаб R, характеризующий
максимальный разброс в облаке данных
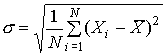 ,
, 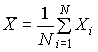 ,
, ![]() .
.
Нормировка всех
признаков на R приводит к тому, что все облако данных заключается в шар
единичного радиуса, а соответствующая формула предобработки имеет вид:
![]() , где
, где ![]() – новые и старые
значения векторов признаков.
– новые и старые
значения векторов признаков.
Если в качестве
масштаба выбрана s , то соответствующая формула предобработки (нормировка
на “единичную дисперсию”) имеет вид:
![]() .
.![]() (3.1)
(3.1)
Если выборка может
считаться полученной из нормального распределения, то в шаре с центром в ![]() радиусом s находится около двух третей от
числа точек данных.
радиусом s находится около двух третей от
числа точек данных.
Поскольку
для экологических данных диапазоны значений для разных признаков очень сильно
отличаются друг от друга, то разумно для каждого из признаков применять
собственный масштаб, т.е. частные статистики j-го показателя s j, Rj и ![]() . Эти
нормировки не являются “изотропными”, то есть они сжимают облако данных в
некоторых направлениях сильнее, в некоторых – меньше. Однако, несмотря на некоторое нарушение структуры
данных (взаимных расстояний), такой подход считается общепринятым.
. Эти
нормировки не являются “изотропными”, то есть они сжимают облако данных в
некоторых направлениях сильнее, в некоторых – меньше. Однако, несмотря на некоторое нарушение структуры
данных (взаимных расстояний), такой подход считается общепринятым.
Возникает
естественный вопрос: какая из нормировочных формул предпочтительнее. Например,
наиболее популярная линейная нормировка по "минимаксу"
![]() .
.![]() (3.2)
(3.2)
оптимальна, когда значения переменной ![]() плотно и равномерно заполняют интервал, определенный эмпирическим
размахом данных. Но подобный "прямолинейный" подход применим далеко
не всегда. Так, если в данных имеются относительно редкие выбросы, намного
превышающие типичный разброс, именно эти выбросы определят, согласно
формулы 3.2, масштаб нормировки. Это приведет к тому, что основная масса
значений нормированной переменной
плотно и равномерно заполняют интервал, определенный эмпирическим
размахом данных. Но подобный "прямолинейный" подход применим далеко
не всегда. Так, если в данных имеются относительно редкие выбросы, намного
превышающие типичный разброс, именно эти выбросы определят, согласно
формулы 3.2, масштаб нормировки. Это приведет к тому, что основная масса
значений нормированной переменной ![]() сосредоточится
вблизи нуля:
сосредоточится
вблизи нуля: ![]() .
.
В связи с этим,
надежнее ориентироваться при нормировке не на экстремальные значения, а на
типичные, т.е. статистические характеристики данных, такие как среднее и
дисперсия и вести расчет по формуле (3.1). Однако в этом случае нормированные
величины не принадлежат гарантированно единичному интервалу, более того, максимальный
разброс значений ![]() заранее не известен.
Для входных данных статистических моделей это может быть и не важно, но
выходные переменные часто используются в качестве эталонов и очень удобно
ограничить диапазон их изменения на интервале от 0 до 1. Естественный выход из
этой ситуации - использовать для предобработки нелинейное
функциональное преобразование данных. Например, преобразование с помощью
сигмоидной функции
заранее не известен.
Для входных данных статистических моделей это может быть и не важно, но
выходные переменные часто используются в качестве эталонов и очень удобно
ограничить диапазон их изменения на интервале от 0 до 1. Естественный выход из
этой ситуации - использовать для предобработки нелинейное
функциональное преобразование данных. Например, преобразование с помощью
сигмоидной функции
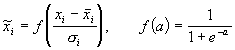
качественно нормирует основную массу данных одновременно гарантируя, что ![]() .
.
Другим вопросом,
представляющим интерес для обсуждения, является формулировка понятий “эквивалентности”
и “коэквивалентности” различных формул нормировки. Согласно теореме Б.И.
Семкина и В.И. Двойченкова [4], два вектора пронормированных значений ![]() и
и ![]() , полученных по различным формулам, эквивалентны, если их
компоненты связаны монотонно возрастающей зависимостью j , т.е.
, полученных по различным формулам, эквивалентны, если их
компоненты связаны монотонно возрастающей зависимостью j , т.е. ![]() = j (
= j (![]() ). Примером такой
функции j является линейное преобразование
). Примером такой
функции j является линейное преобразование ![]() = a + b ×
= a + b × ![]() , позволяющее любые
пронормированные значения умножить, разделить или сложить с некоторым
постоянным числом и при этом предупорядоченность данных нисколько не изменится
(меняется лишь масштаб шкалы измерения). Например, легко увидеть, что являются
эквивалентными между собой оба вектора пронормированных значений полученных по
формулам (3.2) и
, позволяющее любые
пронормированные значения умножить, разделить или сложить с некоторым
постоянным числом и при этом предупорядоченность данных нисколько не изменится
(меняется лишь масштаб шкалы измерения). Например, легко увидеть, что являются
эквивалентными между собой оба вектора пронормированных значений полученных по
формулам (3.2) и
![]()
где ![]() - "наилучшие (или наихудшие) для каждого показателя оценочные
значения (например, наиболее благоприятные для целей строительства, сельского
хозяйства и др. климатические характеристики, величины углов наклона местности
и т. д.)" [5]. Мы не хотим оспорить тезис, что вторая "нормировка
дает возможность выразить отклонения всей системы показателей от наилучших или
наихудших оценочных значений и тем самым правильнее с содержательных позиций их
соизмерить между собой". Однако визуально картограммы показателя,
обработанного по обеим формулам нормировки, будут совершенно идентичны.
- "наилучшие (или наихудшие) для каждого показателя оценочные
значения (например, наиболее благоприятные для целей строительства, сельского
хозяйства и др. климатические характеристики, величины углов наклона местности
и т. д.)" [5]. Мы не хотим оспорить тезис, что вторая "нормировка
дает возможность выразить отклонения всей системы показателей от наилучших или
наихудших оценочных значений и тем самым правильнее с содержательных позиций их
соизмерить между собой". Однако визуально картограммы показателя,
обработанного по обеим формулам нормировки, будут совершенно идентичны.
Однако вернемся к
практическим решениям. Введем такое понятие, как нормированная шкала
(НШ) показателя, которая характеризуется следущими свойствами:
1.
для
всех показателей, преобразованных в НШ, устанавливается единый диапазон области
существования, варьирующийся от Bmin до Bmax ;
2.
распределение
вариационного ряда показателя по шкале НШ соответствует принципу максимума
энтропии каждой из входных переменных.
В рамках текущей
версии системы REGION в качестве НШ была принята порядковая шкала, в которой Bmin
= 1, а Bmax = Kb, где Kb
- размерность шкалы (количество градаций). Из соображений унификации для большинства
исходных показателей, измеренных в метрических шкалах, Kb
была принята равной 6. Размерность Kb для показателей,
изначально измеренных в порядковых или номинальных шкалах, выбиралась каждый
раз исходя из специфики нормируемых данных.
Выбор 6-бальной
нормировочной шкалы основан на тех же теоретических соображениях, что и
традиционные алгоритмы нормировки. Действительно, диапазон варьирования
результирующих значений, полученных после преобразования исходных переменных
(т.е. размерность Kb), не имеет никакого принципиального
значения ни для существа проблемы, ни для характера последующего использования
пронормированных выборок в ходе статистического моделирования. Легко видеть,
например, что НШ от 1 до 6 легко может быть преобразована
в более популярную нормировочную шкалу 0 ¸ 1 по формуле
bi' =(bi - Bmin)/(Bmax-Bmin),
где bi' - значение от 0 до 1.
Поскольку так же
легко реализуется и обратный переход, все множество нормировочных шкал можно
считать эквивалентными.
Другим поводом для
обсуждения качества нормировки является возможная потеря точности при переходе
от метрической шкалы к порядковой. Однако, как
показала практика, погрешность большинства исходных эколого-экономических
данных столь велика, что ошибка измерения практически сопоставима с величиной
самого натурального показателя. В связи с этим можно предположить, что переход
к оценке большинства анализируемых показателей в 6-бальной шкале не приведет к
качественным информационным потерям.
Решающим
преимуществом НШ в виде стандартной ординальной шкалы являются удобство
визуализации пространственного распределения индивидуальных и комплексных
показателей на картосхемах изучаемого региона: человеческий глаз уверенно может
различать контрастную раскраску карт, спектр которой не превышает 6-8 цветов.
Покажем, что общий
принцип, которым следует руководствоваться на этапе нормирования и квантования
числовых переменных, состоит в максимизации энтропии входных и выходных
переменных. Допустим, что в результате перевода всех данных в числовую форму и
последующей нормировки все признаки отображаются в единичном кубе. Задача
построения математических моделей заключается в том, чтобы найти статистически
достоверные зависимости между входными и выходными переменными. Единственным
источником информации для статистического моделирования являются примеры из
обучающей выборки. Чем больше бит информации принесет каждый пример - тем лучше
используются имеющиеся в нашем распоряжении данные.
Рассмотрим
произвольный вектор предобрабатываемых данных: ![]() . Среднее количество информации, приносимой каждым примером
. Среднее количество информации, приносимой каждым примером ![]() , равно энтропии распределения
значений этого показателя:
, равно энтропии распределения
значений этого показателя:
![]()
Если эти значения
сосредоточены в относительно небольшой области единичного интервала,
информационное содержание такой компоненты мало. В пределе нулевой энтропии,
когда все значения переменной совпадают, эта переменная не несет никакой
информации. Напротив, если значения переменной ![]() равномерно распределены в заданном интервале, количество
информации, вносимой такой переменной, максимально.
равномерно распределены в заданном интервале, количество
информации, вносимой такой переменной, максимально.
В соответствии с
изложенным общим принципом, мы должны стремиться к тому, чтобы максимизировать
энтропию закодированных данных. В то же время известно, что из всех
статистических функций распределения, определенных на конечном интервале,
максимальной энтропией обладает равномерное распределение. Применительно
к случаю сведения численной шкалы к порядковой (а именно так можно трактовать
процесс "квантования" или "баллирования") в ЭИС REGION был
принят следующий практический рецепт преобразования переменных. Общий
диапазон допустимых значений показателя разбивается на
![]() отрезков
- по числу классов - с длинами пропорциональными числу примеров каждого класса
в исходной выборке:
отрезков
- по числу классов - с длинами пропорциональными числу примеров каждого класса
в исходной выборке: ![]() , где
, где ![]() - число примеров класса
- число примеров класса ![]() , а
, а ![]() - общее число примеров.
Центр каждого такого отрезка будет являться численным значением для
соответствующего ординального класса (см. рис. 5).
- общее число примеров.
Центр каждого такого отрезка будет являться численным значением для
соответствующего ординального класса (см. рис. 5).
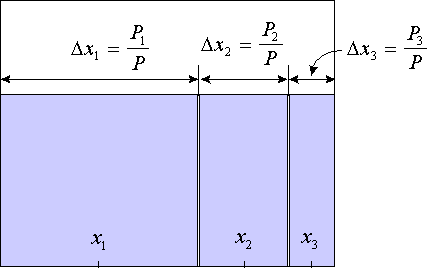
Рис.5.
Илюстрация способа кодирования кардинальных переменных с учетом количества
примеров каждой категории.
При таком способе
“оцифровки” все выделенные классы будут нести примерно одинаковую
информационную нагрузку. Выражаясь точнее, перевод признака, измеренного в
метрической шкале, в систему порядковых переменных ("баллов") будет
сопровождаться наименьшими потерями информации.
Если в ходе
анализа установлено, что мы имеем дело с равномерным распределением данных, то
естественным способом деления на диапазоны области существования [a,
b] анализируемой переменной xq является
выделение k одинаковых отрезков. Во всех остальных случаях выделение
интервалов осуществляется, исходя из условия равенства площадей фигур,
образованных вертикальными секущими от граничных значений до кривой функции
плотности распределения f(xq).
Другой проблемой
ординации исходных показателей является учет характера связи каждого из них с
некоторой целевой функцией обобщенного "экологического состояния". В
ряде случаев вывод о причинно-следственной направленности этой связи более или
менее бесспорен. Например, логично предположить, что рост любых показателей
заболеваемости населения или развитие патологических изменений в органах и
тканях живых организмов однозначно свидетельствует об ухудшении экологического
состояния. Тогда территориям, имеющим самый низкий уровень заболеваемости,
может быть присвоен балл 1, а там, где заболеваемость достигает максимальной
отметки - балл 6. В большинстве случаев показатели, отражающие техногенное
загрязнение территории, водоемов и воздушного бассейна,
"оцифровываются" по аналогичному принципу. Однако,
в общем случае можно выделить три основных варианта функциональной связи
показателя с обобщенным критерием экологического состояния:
1.
с
увеличением значения анализируемого показателя оценка экологического
благополучия увеличивается;
2.
эта
связь имеет антагонистический характер - чем выше показатель, тем хуже
экологическое состояние (на нашем материале - наиболее частый случай);
3.
показатель
распределен унимодально и имеет отчетливо выраженный экологический экстремум
(минимум или максимум).
Для некоторых
показателей выполнены в разной мере тщательные исследования количественного
или, хотя бы качественного характера такой зависимости. Например, на рис. 6
представлено соотнесение диапазона варьирования трех широко известных
гидрохимических показателей со шкалой комплексной экологической классификации
качества поверхностных вод суши по О.П.Оксиюк и В.Н.Жукинскому [6], состоящей
из 9 разрядов. Показаны все три основных варианта функциональной связи
измеряемых переменных с этой весьма распространенной обобщенной оценкой
экологического состояния водоемов (как и в нашем случае, разряды классификации
тем выше, чем ниже качества вод).
|
Прозрачность,
м |
|
|
|
Азот
аммонийный, мг/л |
|
рН |
|
|
|
Биомасса
фитопланктона, мг/л |
Рис 6.
Деление по диапазонам некоторых показателей качества
поверхностных вод суши (по оси ординат – разряды качества вод по классификации
О.П.Оксиюк и В.Н.Жукинского: 1 - предельно чистые, 2а – очень чистая, 2б –
вполне чистая, 3а – достаточно чистая, 3б – слабо загрязненная, 4а – умеренно
загрязненная, 4б – сильно загрязненная. 5а – весьма грязная, 5б – предельно
грязная)
Наибольшие
трудности вызывает анализ показателей, имеющих экологический экстремум. В этом случае деление на интервалы и отчет баллов приходится
осуществлять в обе стороны от условного нуля, за который принимается выявленный
минимум: например, для показателя pH баллу 1 соответствует диапазон от 6.9 до
7.1, баллу 2 - от 6.1 до 6.9 или от 7.1 до 7.9 , а баллу 6 - менее 5.3 или
более 8.7. При этом характер колоколообразной зависимости является
скорее правилом, чем специфическим явлением, если принять во внимание основные
положения факториальной экологии: закон минимума Либиха и закон лимитирующего
фактора Шелфорда [7].
Несмотря на
огромное количество имеющейся литературы о влиянии тех или иных поллютантов на
особенности жизненных циклов биологических объектов, как отмечал Д.М.
Розенберг, “выявленные закономерности основываются, как правило, на
косвенных показателях, а не на процедурах, которые предполагают тщательную
проверку той или иной гипотезы”. Например, согласно той же классификации
О.П.Оксиюк и В.Н.Жукинского, качество воды монотонно ухудшается при росте
биомассы фитопланктона (см. рис. 6), однако, мысленно исключив из трофических
цепей фитопланктон, мы получим вместо водоема "экологическую
пустыню". Другой пример - индекс биологического разнообразия, который
традиционно считается сопутствующим гармоничному и устойчивому развитию
экосистем, однако в отношении монокультурных агроценозов он свидетельствует
лишь о большом количестве сорняков. Трудно определить, скажем, оптимальное
количество кроликов, которое должно приходиться на 1 кв. км сельхозугодий: с
одной стороны, австралийский опыт свидетельствует о том, что их не должно быть
много, а, с другой стороны, кролик - вполне мирное и весьма полезное животное.
Оценка характера
зависимости при преобразовании исходных показателей в нормализованную шкалу
осушествлялся в ЭИС REGION в ходе специализированной человеко-машинной
процедуры, учитывающей:
1.
мнения
коллектива экспертов в данной конкретной предметной
обрасти и имеющиеся литературные источники;
2.
механизмы
системной самоорганизации, обеспечивающие формальный анализ связи вновь
включаемого показателя с уже имеющимся комплексом данных.
Сущность
формально-аналитических методов нахождения оптимальных диапазонов нормирования
показателя заключается в следующем. Пусть нам необходимо преобразовать в НШ
последовательность объектов i = 1,2,…,m, обладающих
признаком xq , который принимает значения на
отрезке [a, b]. Предположим, что в ЭЭС уже
существует некоторый другой (ранее загруженный) индивидуальный показатель (или
обобщенный комплекс из некоторого их подмножества), который мы можем принять в
качестве некоторого эталона экологического состояния. Тогда с помощью этого
вектора-эталона каждая величина xqi может быть
отнесена к одному из n классов измерений D1,
D2, …, Dn , l =
1,2,…,n. Введем разбиение d диапазона
существования признака xq [a, b]
на некоторое заранее заданное количество интервалов k, границы
которых заранее не определены.
Задача состоит в
том, чтобы найти такое разбиение d на градации, которое
наилучшим образом подчеркивает дискриминирующую сущность исходной априорной
классификации измерений D1, D2,
…, Dn. Первый алгоритм основан на максимизации
информационной меры дивергенции, введенной С.Кульбаком [8], которая
имеет смысл средней меры различия двух эмпирических распределений. Метод
формализован А.А.Генкиным [9] и является основой "Оболочки Медицинских
Интеллектуальных систем".
Обозначим через pj(xq
|Ds) частоту попадания значения показателя xq
из подмножества { xq
}Ds в j-й диапазон ( j =
1,2,…,k ). Тогда по первому алгоритму для двух классов Ds
и Dl в качестве наилучшего разбиения диапазона [a,
b] на k отрезков выбирается такое, которое
максимизирует значение дивергенции Кульбака:
![]()
Граничные значения
интервалов легко находятся как полусумма смежных отсортированных значений xqi
обучающей выборки, принадлежащих разным диапазонам.
В общем случае n
классов максимизируется величина:
![]() .
.
Получаемое таким
образом разбиение вместе с вероятностями появления значений признака в
соответствующих интервалах pj(xq|Ds)
называется интервальной структурой [9].
В.Н. Вапником с
соавторами [10] представлен более общий алгоритм
нахождения наилучшего разбиения, основанный на минимизации шенноновской
энтропии и определяющий как границы диапазонов, так и оптимальное число
градаций k.
Пусть существуют
условные вероятности принадлежности x к каждому из n
классов:
P(D1 | xq), P(D2
| xq), …, P(Dn |
xq).
Тогда для каждого
фиксированного значения признака xqi может быть
определена энтропия как мера неопределенности принадлежности вектора x
к тому или иному классу:
![]()
Среднее по мере P(xq)
значение энтропии есть : ![]() .
.
При разбиении d анализируемого диапазона [a, b] на k
интервалов каждая величина численной шкалы xqi будет
принимать одно из к значений порядковой
шкалы c(1), c(2), c(k).
Тогда средняя энтропия может быть записана в виде
![]()
Для того, чтобы оценить энтропию H(k),
необходимо рассчитать вероятности P(Dl | c(j))
и P(xq = c(j)) по обучающей
последовательности, для чего воспользуемся байесовскими оценками:
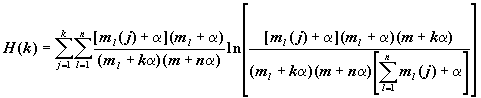 , (3.3)
, (3.3)
где a - константа алгоритма, m - объем обучающей выборки, ml
- число элементов l-го класса в выборке, ml (j)
- число элементов l-го класса, входящих в j-й
диапазон разбиения.
Задача состоит в
том, чтобы найти такое разбиение d интервала численной
переменной xq [a, b] на
градации и определить их число k* , которое наилучшим образом
подчеркивает дискриминирующую сущность исходной априорной классификации, поскольку
максимизируется количество информации, содержащейся в сообщении о
принадлежности вектора x к тому или иному классу:
J(k*) = Hапр
- H(k*),![]() (3.4)
(3.4)
где 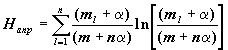
Представленные
алгоритмы реализуются, в той или иной мере, по схеме полного перебора. Например, алгоритм В.Н.Вапника оформлен как процедура многократного
дробления-склейки градаций-претендентов, пока не будет найдено разбиение d и число диапазонов k* ,
доставляющие максимум выражению (3.4). Часто разумно пытаться уменьшить
количество градаций k* и после достижения минимума по k
функции H(k*), но лишь до тех пор, пока величина J(k*)
не уменьшится в (1- d ) раз, где d - параметр
алгоритма.
Обоснованность результатов нахождения оптимальных границ диапазонов квантования
данных по описанным алгоритмам зависит от качества априорного деления
координат преобразуемого вектора на классы, которое повышается по мере
наполнения информационной системой данными (смысл самоорганизации).
Литература
1.
Ноулер Л., Хауэлл Дж., Голд Б. и др. Статистические методы контроля качества продукции. – М.:
Изд-во стандартов, 1989. – 96с
2.
Воpобейчик Е.Л., Садыков О.Ф., Фарафонтов М.Г. Экологическое нормирование техногенных загрязнений
наземных экосистем (локальный уровень). Екатеринбург: Наука, 1994. 280 с.
3.
Шуйский В.Ф., Занцинская Т.П., Петров Д.С. Количественная оценка и нормирование сложных
антропогенных воздействий на макрозообентос // Сб. научных трудов ГосНИОРХ –
вып.326 – 2000 — С. 137–144 (соавторы,)
4.
Сёмкин Б.И., Двойченков
В.И. Об эквивалентности мер сходства и различия // Исследование систем. –
Владивосток: ДВНЦ АН СССР, 1973. С. 18-43.
5.
Тикунов B.C.
Классификации в географии: ренессанс или увядание? (Опыт формальных
классификаций). - Москва-Смоленск, Изд-во СГУ, 1997, 367 с.
6.
Оксиюк О.П., Жукинский В.Н., Брагинский Л.П. и др. Комплексная экологическая классификация качества
поверхностных вод суши // Гидробиол. журн. 1993. Т. 29. № 4. С. 62-77.
7.
Розенберг Г.С., Мозговой Д.П., Гелашвили Д.Б. Экология. Элементы теоретических конструкций
современной экологии. – Самара: СамНЦ РАН, 1999. – 396 с.
8.
Кульбак С. Теория
информации и статистика. – М.: Наука, 1967. – 408 с.
9.
Генкин А.А. Новая
информационная технология анализа медицинских данных. – СПб: Политехника, 1999.
– 191 с.
10. Алгоритмы и программы восстановления
зависимостей. – М.: Наука, 1984. – 816 с.
4.
Методы классификации и редукции данных
Основной вопрос,
которым задается пользователь информационной системы (эколог-исследователь или
лицо, принимающее решение в области планирования природоохранных мероприятий),
формулируется следующим образом:
"Возможно ли построить на имеющемся множестве
данных сколько-либо разумную (естественную, полезную) систему отношений?"
Поэтому
подавляющее большинство разрабатываемых статистических моделей, так или иначе связано с классификацией. У истоков любой модели всегда
лежит замысел человека научить компьютер "отличать одно от другого",
т.е. по значению прогнозируемого показателя-отклика явно или неявно оценить некоторую категориальность изучаемого объекта,
процесса или явления. Например, хочется:
а) определить степень ("класс") техногенного преобразования участков
территории;
б) узнать, является ли скорость депонирования фосфора большой или маленькой;
в) предположить, что в ходе эволюции плотность популяции будет возрастать или
убывать;
г) оценить, насколько опасным для здоровья является действие того или иного
химического вещества,
т.е. в конечном итоге что-то расклассифицировать. Получив
результаты моделирования, исследователь чаще всего начинает выполнять
диагностику, т.е. сравнивать между собой изучаемые объекты, процессы или
явления по выделенным отличительным признакам классов (или “дискриминирующим
правилам”). Здесь было бы кстати упомянуть, что само
классифицирование является своеобразной “сверткой” исходных информационных
таблиц, поскольку число выделяемых классов всегда меньше, чем уникальных
объектов, т.е. в итоге получается по возможности лаконичное, наглядное и
полезное представление данных в пространстве существенно меньшей
размерности. В то же время, математические методы редукции пространства
признаков сами являются одним из эффективных средств классифицирования.
Кластерный
анализ
Задача кластерного
анализа состоит в выяснении по эмпирическим данным, каким образом элементы
“группируются” или распадаются на изолированные “скопления”, “кластеры” (cluster
(англ.) — гроздь, скопление), причем никаких априорных предположений о
классовой структуре, как правило, не делается. Иными словами, задача —
выявление естественного разбиения на классы, свободного от субъективизма
исследователя, а цель—выделение групп однородных объектов, сходных между собой,
при резком отличии этих групп друг от друга.
Абсолютное
большинство методов кластеризации [1-4] основывается на анализе квадратной и
симметричной относительно главной диагонали матрицы D
коэффициентов сходства (расстояния, сопряженности, корреляции и т.д.) между
объектами исходной матрицы наблюдений:
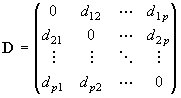
В ЭИС REGION
реализована возможность расчета матрицы D по заданному набору
показателей с использованием различных формул для меры дистанции, выбираемых
пользователем. Наиболее общей формулой для подсчета расстояния в m-мерном
признаковом пространстве между объектами X1 и X2
является мера Минковского [3]:
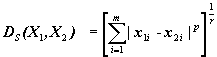
где r и
p – параметры, определяемые исследователем, с помощью
которых можно прогрессивно увеличить или уменьшить вес, относящийся к
переменной i, по которой соответствующие объекты наиболее
отличаются. Параметр p ответственен за постепенное взвешивание
разностей по отдельным координатам, параметр r определяет
прогрессивное взвешивание больших расстояний между объектами.
Мера расстояния
по Евклиду получается, если метрике
Минковского положить r = p = 2, и является,
по-видимому, наиболее общим типом расстояния, знакомым всем по школьной теореме
Пифагора, – геометрическим расстоянием в многомерном пространстве, которое
вычисляется следующим образом:
![]() .
.
Заметим, что
евклидово расстояние может быть вычислено как по исходным, так и по
стандартизованным данным (например, нормированным на интервале от 0 до 1).
При r
= p = 1 метрика Минковского дает "расстояние городских
кварталов" (манхэттенское расстояние), которое является
просто суммой разностей по координатам:
![]() .
.
В большинстве
случаев эта мера расстояния приводит к таким же результатам, что и обычное
расстояние Евклида. Однако отметим, что для нее влияние отдельных больших
разностей (выбросов) уменьшается, так как они не возводятся в квадрат.
При r = p
® ¥ имеем метрику
доминирования (она же, супремум-норма или расстояние Чебышева),
которая вычисляется по формуле:
DT(X1,X2)
= max | x1i – x2i |.
Это расстояние
может оказаться полезным, когда желают определить два объекта как
"различные", если они различаются по какой-либо одной лимитирующей
координате (каким-либо одним измерением).
Отдавая дань
устоявшимся экологическим традициям, в алгоритм формирования матрицы D
был включен еще нескольких десятков выражений, часто применяемых для различных
шкал (меры сходства Жаккара и Съеренсена, коэффициент корреляции Пирсона,
коэффициент Гауэра и т.д.)
Программные
средства ЭИС REGION обеспечивают расчет компонентов матрицы расстояний D
с использованием любой из перечисленных выше концепций или формул, что не имеет
принципиального значения для работы собственно алгоритмов классификации,
которые реализуются с использованием внешних пакетов прикладных программ. С
этой целью реализован вывод сформированной матрицы в файл формата ППП
Statistica 5.5.
Собственно
кластерный анализ включает в себя набор различных алгоритмов классификации,
сутью которых является группировка данных в наглядные структуры (таксоны). К
этому семейству алгоритмов относятся: иерархическое объединение (древовидная
кластеризация), двувходовое объединение, метод К-средних и др.
Пусть исходные
данные — матрица сходства ||d(x, y)|| , где d(х,
у) - некоторая мера близости между каждой парой классифицируемых объектов x
и y. Хорошо известно, что для любого заданного разбиения объектов
на группы и любого e > 0 можно указать метрику, такую, что расстояния
между объектами из одной группы будут меньше e , а между объектами из
разных групп — больше 1/e . Тогда любой разумный алгоритм кластеризации даст
именно заданное разбиение.
Наиболее часто
применяется так называемый агломеративный иерархический алгоритм
“Дендрограмма”, отдельные версии которого отличаются правилами вычисления
расстояния между кластерами. Рассмотрим, к примеру, один определенный алгоритм
— алгоритм средней связи. На первом шаге каждый объект рассматривается как
отдельный кластер. На каждом следующем шаге объединяются две ближайших
кластера. Расстояние между кластерами рассчитывается как средняя связь (отсюда
и название алгоритма), т.е. как среднее арифметическое расстояний между парами
объектов, один из которых входит в первый кластер, а другой — во второй. В
конце концов, все объекты объединяются вместе, и результат работы алгоритма
представляет собой дерево последовательных объединений (в терминах теории
графов), или “Дендрограмму”. Из нее можно выделить кластеры разными способами.
Один подход — исходя из заданного числа кластеров. Другой — из соображений
предметной области. Третий — исходя из устойчивости (если разбиение долго не
менялось при возрастании порога объединения, значит
оно отражает реальность) и т.д.
К алгоритму
средней связи естественно сразу добавить:
1.
алгоритм ближайшего соседа, когда расстоянием между
кластерами считается минимальное из расстояний между парами объектов, один из
которых входит в первый кластер, а другой — во второй;
2.
алгоритм
дальнего соседа, когда расстоянием между кластерами считается максимальное из расстояний между парами объектов, один из
которых входит в первый кластер, а другой — во второй.
3.
невзвешенный
и взвешенный центроидный метод, метод Уорда, использующий методы дисперсионного
анализа для оценки расстояний между кластерами) и др.
Каждый из
описанных алгоритмов (средней связи, ближайшего соседа, дальнего соседа),
порождает бесконечное (континуальное) семейство алгоритмов кластер-анализа. Дело
в том, что величина da (х, у),
a > 0, также является мерой близости между х
и у и порождает новый алгоритм. Если параметр a пробегает отрезок, то получается бесконечно много алгоритмов
классификации. При этом каждое полученное разбиение на классы, разумеется, не
является “реальными”, поскольку отражает, прежде всего, свойства алгоритма, а
не исходных данных.
В качестве
критерия естественности классификации можно рассматривать устойчивость
относительно выбора алгоритма кластер-анализа. Проверить устойчивость можно,
применив к данным несколько подходов, например, столь непохожие алгоритмы, как
“ближайшего соседа” и “дальнего соседа”. Если полученные результаты
содержательно близки, то классификации адекватны действительности. В противном
случае следует предположить, что естественной классификации не существует и
задача кластер-анализа не имеет решения.
Кроме
иерархических методов классификации большое распространение получили также
различные итерационные процедуры, которые пытаются найти наилучшее разбиение,
ориентируясь на заданный критерий оптимизации, не строя при этом полного дерева
(метод К-средних Мак-Кина, алгоритмы "Форель",
"Медиана", "Краб" и т.д.). Итерационный процесс начинается,
как правило, с K случайно выбранных кластеров, а затем изменяется
принадлежность объектов к ним, чтобы: (1) - минимизировать изменчивость внутри
кластеров, и (2) - максимизировать изменчивость между кластерами. Для этих
алгоритмов важной является “проблема остановки”: завершится ли процесс
улучшения положения центра кластера через конечное число шагов или же он может
быть бесконечным.
В качестве
вычислительного примера реализации кластерного анализа сформируем произвольную
многомерную выборку из базы данных по Волжскому бассейну, составляющую
некоторый набор из 15 следующих показателей, полученных по состоянию на
2000-2001 гг. и преобразованных в нормированную шкалу:
|
Наименование |
Шифр |
|
Валовый региональный продукт, млн.руб./чел. |
E_VP |
|
Плотность населения, тыс.чел./кв.км |
E_PN |
|
Производство электроэнергии, млн.кВт в час/чел. |
E_PE |
|
Общие затраты на природоохранные
мероприятия в различных средах |
E_ZP |
|
Внесение минеральных удобрений, кг/га |
C_MU |
|
Сумма использованных пестицидов, кг/га всей посевной площади |
C_SP |
|
Сброс загрязненных сточных вод, куб.м/чел. |
Z_SV |
|
Удельный вес проб, не
отвечающих гигиеническим номативам по санитарно-токсикологическим показателям |
Z_KP |
|
Суммарные выбросы в атмосферу загрязняющих
веществ, т/чел. |
Z_VA |
|
Выбросы в атмосферу от автомобильного
транспорта,т/чел. |
Z_AA |
|
Образование токсичных отходов, т/чел. |
Z_TO |
|
Общая заболеваемость на 1000 чел. |
M_OZ |
|
Болезни органов дыхания на 1000 чел. |
M_OD |
|
Смертность от рака кожи на 100 тыс. чел. |
M_RK |
|
Число умерших детей в возрасте до 1 года на
1000 родившихся |
M_DS |
На рис. 7 приведены
дендрограммы иерархической классификации административных единиц Волжского
бассейна с использованием различных методов и метрик для матрицы расстояний объектов
по всему представленному списку показателей. На рис. 8 показано разбиение тех же точек на 5
заданных классов с использованием итеративной процедуры к-средних
Мак-Кина, локализующей сгущения в многомерном пространстве из 15 признаков.
Характер полученных классификаций может быть оценен как умеренно размытый. Все
алгоритмы устойчиво подчеркивают абсолютную уникальность Московской обл., хотя
метод дальнего соседа наделил подобной специфичностью и Башкирию. Также
единодушно подчеркивается относительная близость Нижегородской и Кировской,
Калужской и Пензенской, Мари Эл и Ульяновской областей.
|
а)
Метод ближнего соседа (ось Y - евклидово расстояние) |
|
б)
Метод дальнего соседа (ось Y - евклидово расстояние) |
|
в) Метод
средней связи (ось Y - манхеттенское расстояние) |
|
г)
Метод Уорда (ось Y - манхеттенское расстояние) |
Рис. 7. Дендрограммы классификации административных
территорий Волжского бассейна
с использованием различных методов и мер расстояний (условные обозначения
областей - см. на рис. 8 )
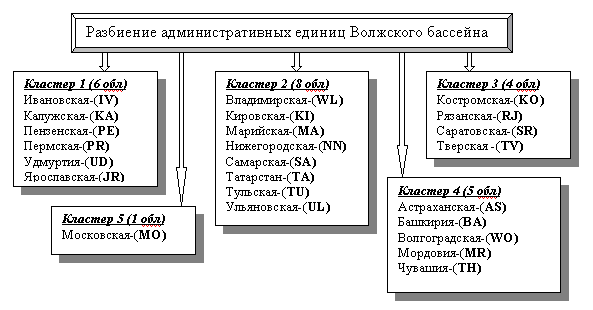
Рис. 8. Разбиение административных территорий
Волжского бассейна на классы с использованием алгоритма к-средних и
расстояния по Евклиду в пространстве 15 показателей
Редукция данных методами факторного
анализа и многомерного шкалирования
Для понижения
размерности исходной информации (редукция данных) используются различные
методы: факторный анализ и выделение главных компонент, многомерное
шкалирование, нейросетевое моделирование, саморганизующиеся карты Кохонена.
Сущность факторного
анализа заключается в представлении исходных показателей Х в виде
некоторой совокупности латентных переменных F, называемых факторами:
![]() , где p<<m,
, где p<<m,
При этом
формируется оптимальное пространство новых ортогональных (взаимно
некоррелированных) переменных без существенной потери содержательной
информации, содержащейся в исходных данных. В основу анализа главных компонент
положено, что факторы являются линейной комбинацией исходных показателей.
![]()
где ![]() – главные компоненты,
– главные компоненты, ![]() –
факторные нагрузки;
–
факторные нагрузки;
Получаемые факторы
упорядочены по степени объяснения статистической вариации в пространстве
показателей. Допустим, что облако объектов является выборкой из генеральной
совокупности, подчиненной закону нормального распределения. Значительное
(например, более 60%) число всех объектов находится в области, представляющей
собой эллипсоид рассеяния, центрированный в точке сгущения с осями, определяющимися
собственным значениям ковариационной матрицы. Линия, совпадающая с направлением
наибольшей по длине оси эллипсоида рассеяния облака и ориентированная вдоль
наибольшей дисперсии облака данных, соответствует первой главной компоненте.
Процедура выделения
последующих главных компонент подобна вращению,
максимизирующему в итоге остаточную дисперсию исходного пространства признаков.
Вычисления основаны на определении собственных значений
(λ) корреляционной матрицы (R) исходных показателей. Выбор
количества факторов (главных компонент) - произвольное решение, однако
существуют критерий Кайзера и критерий каменистой осыпи
Кэттеля.
Наиболее
практически ценной является плоскость первых двух главных компонент, дающая
возможность представить многомерное облако данных в виде наглядной двумерной
картинки. Такая визуализация позволяет выявить основные закономерности,
присущие набору данных: его внутреннюю структура,
изначальное разделение данных на классы (если таковое имеется), существование
различных зависимостей между признаками и так далее.
Рассмотрим пример визуализации областей
Волжского бассейна на основе метода главных компонент в пространстве 15
переменных, использованных для иллюстрации кластерного анализа. После редукции
исходного пространства к 2 главным компонентам полученное разложение объясняет
39,5 % статистической вариации рассматриваемых показателей. Интерпретировать
полученные факторы можно с помощью графика факторных нагрузок (рис. 9):
очевидно, что первый фактор определяется, в основном, валовым региональным
доходом (E_VP), плотностью населения (E_ PN) и детской смертностью
(M_DS), а второй фактор - совокупностью остальных медицинско-статистических
показателей, загрязнением (Z_KP) и сбросом сточных вод (Z_SV) .
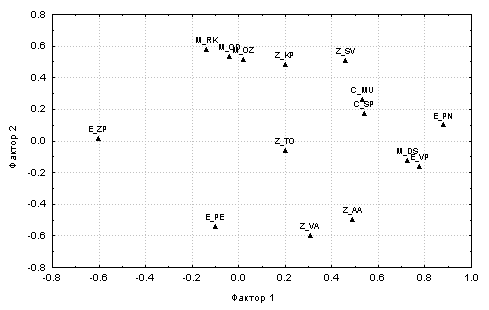
Рис.
9. График отображения факторных нагрузок (обозначения показателей - по тексту)
Используя
рассчитанные факторные нагрузки как коэффициенты линейного преобразования,
можно сформировать редуцированную матрицу исходных данных, где столбцами
являются новые факторизованные признаки. Анализ двухмерной визуализации
взаимного расположения объектов на рис. 10 показывает, что в целом в результате
редукции подтверждаются структурные соотношения, установленные в ходе
кластерного анализа: по экстенсивным показателям (фактор 1) выделяется
Московская обл., а по относительной экологической стабильности (фактор 2 -
Башкирия).
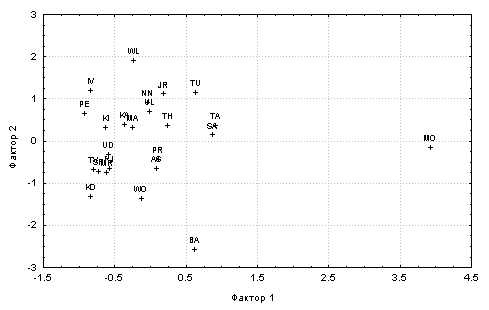
Рис.
10. Отображение территориальных единиц Волжского бассейна в
пространстве двух главных факторов, полученный методом главных компонент
(обозначения те же, что и на рис. 8)
Моделирование
данных с помощью линейных факторов является оптимальными лишь в случае близкого
к нормальной выборке облака точек в пространстве исходных переменных. Поэтому
особый интерес представляют принципиально нелинейные способы редукции и
визуализации, учитывающие некоторые важные характеристики структуры данных и позволяющие
построить эффективную технологию анализа таблиц реальных показателей.
Одним из
нелинейных методов отображения векторов ![]() из
многомерного пространства описания Rm в пространство R2
является алгоритм многомерного шкалирования (МШ) данных [5], основанный, как и
кластерный анализ, на целенаправленном преобразовании матриц сходства D,
заранее сформированных на исходном множестве показателей. МШ – это не столько
определенная математическая процедура, сколько способ наиболее эффективного
размещения объектов, приближенно сохраняющий расстояние между ними в новом
пространстве признаков, размерность которого существенно меньше исходного. Хотя
методы многомерного шкалирования не связаны никакими ограничениями по закону
распределения многомерных векторов, его основным недостатком является
отсутствие точной математической зависимости для функции ошибки отображения
данных, а именно – если совершен переход из исходного многомерного пространства
Rm в Rp, то обратное отображение
невозможно.
из
многомерного пространства описания Rm в пространство R2
является алгоритм многомерного шкалирования (МШ) данных [5], основанный, как и
кластерный анализ, на целенаправленном преобразовании матриц сходства D,
заранее сформированных на исходном множестве показателей. МШ – это не столько
определенная математическая процедура, сколько способ наиболее эффективного
размещения объектов, приближенно сохраняющий расстояние между ними в новом
пространстве признаков, размерность которого существенно меньше исходного. Хотя
методы многомерного шкалирования не связаны никакими ограничениями по закону
распределения многомерных векторов, его основным недостатком является
отсутствие точной математической зависимости для функции ошибки отображения
данных, а именно – если совершен переход из исходного многомерного пространства
Rm в Rp, то обратное отображение
невозможно.
Пример визуализации областей Волжского
бассейна методом многомерного шкалирования с использованием матрицы евклидовых
дистанций в пространстве 15 показателей представлен на рис. 11.
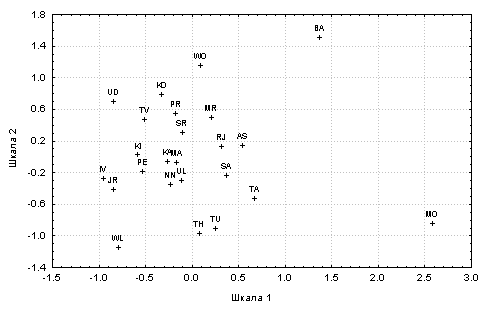
Рис.
11. Отображение территориальных единиц Волжского бассейна в пространстве двух
шкал, построенных методом многомерного шкалирования на основе расстояния Евклида
(обозначения те же, что и на рис. 8)
Как и в случае с
кластерным анализом, построение факторных моделей и реализация процедур
многомерного шкалирования осуществлялась с использованием внешних модулей ППП
Statistica 5.5.
Автоассоциативные
нейронные сети
Как упоминалось в
разделе 1, эффективным способом глубокого анализа структуры исходных данных и
редукции пространства с учетом нелинейных искажений осей максимальной вариации
является нелинейный вариант метода главных компонент, основанный на применении
автоассоциативных сетей.
Автоассоциативная
сеть – это сеть, предназначенная для воспроизведения на выходе своих же
сигналов. У такой сети число выходов совпадает с числом входов, а все нейроны
имеют особое свойство. Если число элементов промежуточного слоя сделать меньше
числа входов/выходов, то это заставляет сеть "сжимать" информацию,
представляя ее в меньшей размерности. Для синтеза искусственных нейронных сетей
в качестве интеллектуального дополнения к ЭИС REGION используется нейросетевой процессор
Statistica Neural NetWorks 2.0.
Для того чтобы
осуществить нелинейное понижение размерности исходной матрицы показателей по
областям Волжского бассейна, используемой в предыдущем примере, выберем
пятислойную сеть (см. рис. 12). Ее средний (третий) слой служит для уменьшения
размерности, а соседние с ним слои, отделяющие его от входного и выходного
слоев, выполняют нелинейные преобразования. Выполним следующие действия:
1.
построим
автоассоциативную сеть – персептрон с пятью слоями, как показано на рис. 12,
причем значения, которые подаются на вход 15 нейронов 1-го
слоя соответствуют значениям на выходе нейронов 5-го слоя;
2.
обучим
автоассоциативную сеть на имеющейся выборке с использованием любого
итеративного алгоритма (для определенности используем метод сопряженных
градиентов);
3.
удалим
два последних слоя автоассоциативной сети и на выходе двух нейронов третьего
слоя получим сеть для препроцессирования, с помощью которой генерируется версия
входных данных в уменьшенной размерности: те же строки исходной таблицы, относящиеся
к разным территориальным участкам, но количество варьируемых признаков сведено
от 15 к 2 без существенной потери информации.
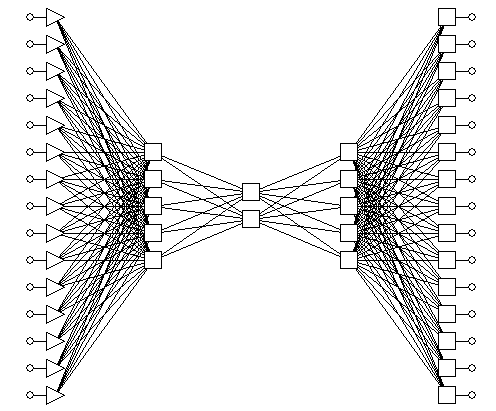
Рис.
12. Автоассоциативная сеть, использованная для понижения размерности матрицы из
15 показателей по областям Волжского бассейна
Двухмерная
визуализация классифицируемых объектов в осях полученных главных факторов,
представленная на рис. 13 , в целом сохраняет основную
пространственную предупорядоченность территориальных единиц Волжского бассейна,
полученную в ходе кластерного анализа, с помощью главных компонент и
многомерного шкалирования (см. рис. 7 - 11). Некоторая имеющая место
модификация пространственного расположения точек можно объяснить учетом
нелинейных искажений исходного пространства переменных.
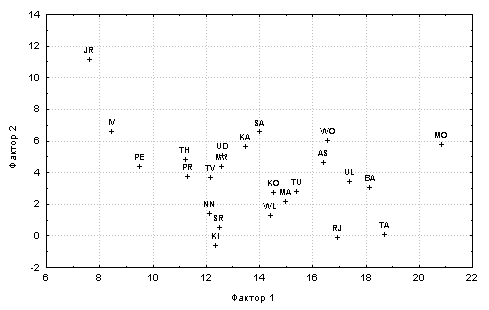
Рис. 13
. Отображение территориальных единиц Волжского бассейна в пространстве двух
главных факторов, полученный методом нейросетевого моделирования (обозначения
те же, что и на рис. 8)
Самоорганизующиеся карты Кохонена
Выполним предварительно небольшое формальное
обобщение вышеизложенного.
Задача
классификации [7] заключается
в разбиении объектов на классы, причем основой для разбиения служат векторы
параметров объекта. Объекты в пределах одного класса считаются эквивалентными с
точки зрения критерия разбиения. Сами классы часто бывают
неизвестны заранее, а формируются динамически. Т.е. и сети Кохонена и все
рассмотренные выше методы реализуют концепцию "классификации без
учителя": состав и количество полученных классов зависят только от
предъявляемых объектов, и поэтому добавление нового объекта или исключение
имеющегося может вызвать корректировку системы классов.
Будем
характеризовать объекты, подлежащие классификации, вектором параметров хр
Î X .
Введем также множество классов {Cm} в пространстве
классификации С: (С1È C2...
È CM) Ì C. Пространство
классов может не совпадать с пространством объектов Х и,
как правило, имеет меньшую размерность. Определим ядра классов {cm}
= с1,...,сm в пространстве классов С, как объекты, типические для своего класса.
Введем также меру дистанции d(xp ,сm) — скалярную функцию от объекта и ядра
класса, которая тем меньше, чем больше объект похож на ядро класса. Задавшись
числом классов М, можно поставить задачу классификации: найти M
ядер классов {cm}и разбить объекты {хр}
на классы {Cm}, т.е. построить функцию т(р) таким
образом, чтобы минимизировать сумму мер дистанции:
![]()
Функция т(р), определяющая номер класса по индексу p
множества объектов {хр}, задает разбиение на классы и
является решением задачи классификации.
Выберем евклидову
меру дистанции. В этом случае ядро класса, минимизирующее сумму мер близости
для объектов этого класса, совпадает с центром тяжести объектов:
![]()
где N(m0)
— число объектов хр в
классе wq . Тогда при разбиении на классы должна быть минимизирована
суммарная мера близости для всего множества {хр}
входных объектов:
![]() .
.
Поскольку сумма ![]() ' очень
напоминает взвешенную сумму
' очень
напоминает взвешенную сумму ![]() рассчитываемую формальным нейроном, алгоритм
нахождения приведенного оптимума легко реализуется в виде нейронной сети. Для
этого требуется сконструировать М сумматоров, настраивающих все Dm,p
выходов сети, и интерпретатора, находящего сумматор m с максимальным
выходом.
рассчитываемую формальным нейроном, алгоритм
нахождения приведенного оптимума легко реализуется в виде нейронной сети. Для
этого требуется сконструировать М сумматоров, настраивающих все Dm,p
выходов сети, и интерпретатора, находящего сумматор m с максимальным
выходом.
Таким образом,
нейронная сеть, используемая для классификации, будет иметь М выходов,
равное числу классов. Если выбрать в качестве входных данных вектор параметров
единственного объекта, то результатом работы уже обученной сети будет код
класса, к которому принадлежит предъявленный на входе объект. При этом, чем большее значение принимает выход номер wq,
тем больше "уверенность" сети в том, что входной объект принадлежит к
классу wq.
Рассмотренная сеть
нейронов, использующая евклидову меру близости для классификации объектов,
называется сетью Кохонена (рис.14) и обсуждалась ранее в разделе 1 как
эффективное средство визуализации. Нейроны слоя Кохонена генерируют на выходе
сигналы Dm,p , причем максимальный сигнал соответствует
номеру класса объекта, который был предъявлен на входе, в виде вектора хр.
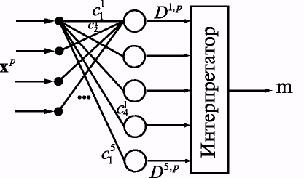
Рис.14
. Сеть Кохонена
В описываемой сети
ядра сm являются весовыми
коэффициентами нейронов. Каждый нейрон запоминает одно ядро класса, и отвечает
за определение объектов в своем классе, т.е. величина выхода нейрона тем
больше, чем ближе объект к данному ядру класса. Общее количество классов
совпадает с количеством нейронов, но, меняя размерность проекционного ячеистого
экрана, можно динамически менять количество классов.
Задача обучения —
настроить все коэффициенты активации и научить сеть активировать один и тот же
нейрон для похожих векторов хр на
входе. Для этого веса сети настраиваются итеративным алгоритмом, который в
целом аналогичен многим известным приемам классификации, но изобилует
различными эвристическими приемами, позволяющими получить устойчивое и
субоптимальное решение за минимальное число итераций. В правила технологии
обучения входят правильное распределение плотности ядер с использованием метода
выпуклой комбинации, искусственное подавление активности нейронов-победителей,
перераспределение весов среди нейронов R-окрестности и т.д. В литературе
представлено детальное описание всех математических аспектов итеративного
алгоритма, что избавляет нас от необходимости приводить детальное его
изложение.
В результате
обучения сети Кохонена строится совокупность карт, каждая из которых
представляет двумерную сетку узлов, размещенных в многомерном пространстве. При
этом используется такое раскрашивание карты, когда цвет каждого нейрона
отражает величину связанного с ним визуализируемого критерия (расстояние между
узлами, вклад того или иного исходного показателя, среднеквадратичную ошибку
квантования и т.д.). Самый простой вариант - использование градаций серого
цвета. В этом случае ячейки, соответствующие узлам карты, в которые попали
элементы с минимальными значениями компонента или не попало вообще ни одной
записи, будут изображены белым цветом, а ячейки, в которые попали записи с
максимальными значениями такого компонента, будут соответствовать ячейке
черного цвета. В принципе, для раскраски можно использовать любую иную
градиентную палитру.
Для формирования
карт Кохонена в системе ЭИС REGION предусмотрен информационный интерфейс с
аналитическим пакетом Deductor Professional - набором приложений,
предназначенных для быстрого и эффективного анализа информации.
Выполним
построение самоорганизующихся карт для анализа пространственного распределения
по территории Волжского бассейна 15 показателей, которые мы использовали в
предыдущих примерах. Как и при применении итерационной процедуры кластеризации методом к-средних Мак-Кина, из всех
возможных разбиений было задано деление на 6 кластеров.
Три карты,
представленные на рис. 15, показывают общие итоги классификации. На карте а)
отображаются группы векторов, расстояние между которыми меньше, чем расстояние
до соседних групп. Иными словами, все элементы карты, входящие в область одного
цвета, имеют сходные между собой признаки и определяют границы областей
кластеров, число которых было задано.
|
а)
Выделенные кластеры ячеек |
|
|
в)
Связь узлов карты с территориальными единицами Волжского бассейна |
|
Рис. 15 . Классификация территориальных
единиц Волжского бассейна
с использованием самоорганизующихся карт Кохонена (обозначения те же, что и на
рис. 8)
На карте б) рис.
15 представлена компонента UMatrix - унифицированная матрица расстояний,
используемая для тонкого анализа структуры кластеров, полученных в результате обучения
карты. Элементы матрицы определяют расстояние между весовыми коэффициентами
нейрона и его ближайшими соседями. Большее значение говорит о том, что данный
нейрон сильно отличается от окружающих и может принадлежать другому классу:
например, можно предположить, что Татарстан имеет меньше оснований относиться к
кластеру 4, чем. Пензенская обл.
На карте в)
представлена маркировка узлов: для каждого нейрона ищется точка в исходном
наборе данных (т.е. территориальная единица Волжского бассейна), ближайшая к
каждому узлу или совпадающая с ним. По сравнению с
аналогичными классификациями, сделанными другими методами, появились
определенные модификации: например, Московская область все же объединилась с
Волгоградской и Башкортостаном, зато оказалась неожиданно подчеркнута
уникальность Рязанской обл. В то же время, по-прежнему вместе Кировская,
Нижегородская, Ульяновская, Самарская области и Татарстан, объединенные 4-м
кластером, а также такие географические антиподы, как Тверская и Саратовская
области (см. кластер 1) .
Построенная
совокупность (атлас, "слоеный пирог) карт отображает также проекции не
только объектов, но и каждого исходного показателя, составляющего многомерные
векторы, на сетку нейронов, которые соответствующим образом окрашиваются
согласно значению того или иного признака. Процесс объяснения структурных
механизмов объединения при помощи самоорганизующихся карт собственно и сводится
к получению этих самых проекций и анализу образующихся групп кластеров. (см. рис. 16)
|
а) Смертность от рака кожи на 100 тыс. чел |
б) Производство электроэнергии, млн.кВт в час/чел. |
|
в) Выбросы в атмосферу от автомобильного
транспорта,т/чел. |
г) Внесение минеральных удобрений, кг/га |
Рис. 16. SOM-карты для анализа вклада
отдельных показателей
в классификацию территориальных единиц Волжского бассейна
Например, можно предположить, что объединение
исходных объектов в области в значительной мере произошло в силу следующих
показателей, являющихся своеобразными "визитными карточками" классов:
1. кластер 3 - высокая смертность от рака
кожи: фиг. а) рис. 16;
2. кластер 2 - большое производство
электроэнергии: фиг. б) рис. 16;
3. кластер 5 - высокий уровнь
автомобилизации: фиг. в) рис. 16;
4. кластер 4 - внесение минеральных
удобрений фиг. г) рис. 16.
Впрочем, подобные выводы так же
полуинтуитивны, как и "предметное наполнение" факторов при анализе
главных компонент.
Литература
(см. также литературу к разделу 1)
1.
Дюран Б., Оделл П.
Кластерный анализ. – М.: Статистика, 1977. – 128 с.
2.
Классификация и
кластер / Под ред. Дж. Вэн-Райзина. – М.: Мир,
1980. – 390 с.
3.
Ким Дж.О., Мьюллер Ч.У, Клекка У.Р. и др. Факторный, дискриминантный и кластерный анализ. – М.:
Финансы и статистика, 1989. – 215 с.
4.
Мандель И.Д.
Кластерный анализ. – М.: Финансы и статистика, 1988. – 176 с.
5.
Краскел Дж.Б. Многомерное шкалирование и другие методы поиска
структуры // Статистические методы для ЭВМ. – М.: Наука, 1986. С. 301-347.
6.
Заенцев
И.В. Нейронные сети:
основные модели (учебное пособие). Воронежский гос. ун-тет, 1999. 76 с.
5.
Введение в "индексологию"; алгоритмы получения комплексных
показателей
В экологии не существует
таких объектов и не изобретено таких “линеек”, совмещение которых позволило бы
путем считывания чисел со шкалы определить, например, объем валовой продукции
экосистемы, ее "биоценозное качество" или темпы сукцессионных
изменений. Экологические измерения почти всегда косвенные или производные.
Экологические величины определяются путем расчета индексных выражений, формула
исчисления которых задается некоторой субъективно определенной схемой
(операциональным определением). Более того, первичные измерения,
имеющие в физике фундаментальное значение (счет, физические измерения веса,
объема, длины особей и т.д.), в экологии, как правило, экологического характера
не имеют. Сравниваемый характер они приобретают лишь после своей свертки
в экологические величины, характеризующие объект на уровне популяции,
трофической группы или биоценоза в целом.
В целом ряде
областей науки при сопоставлении каких-либо данных, характеризующих явление или
процесс во времени и в пространстве, широкое употребление нашли индексы
– относительные статистические величины, показывающие, насколько уровень
изучаемого явления в данных условиях отличается от уровня того же явления в
других условиях. Они олицетворяют попытку относительно просто и практически
целенаправленно рассчитать и соизмерить сложные объекты или системы, состоящие
из непосредственно несопоставимых элементов. Полученные на основе индексного
метода расчетные показатели могут использоваться в более сложных математических
моделях для характеристики развития анализируемых процессов во времени или по
территории, для выявления структуры, взаимосвязей и роли отдельных факторов в
динамике сложных систем.
Остановимся на
способах вычисления так называемых общих индексов, которые представляют собой
вектор значений результирующего комплексного показателя, полученного в
результате информационной свертки (редукции) некоторого подмножества
индивидуальных показателей. К настоящему времени практически
общеупотребительной схемой такого обобщения данных в экологии и экономике
являются методы, основанные на гипотезе аддитивности индивидуальных
вкладов. Получаемый таким образом комплексный показатель представляет собой
вектор той же размерности, что и базовый, каждый i-й компонент которого
вычисляется по одной из следующих формул (алгоритм "Суммация"):
1.
простая
сумма ![]() ;
;
2.
простое
среднее 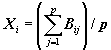 ;
;![]() (5.1)
(5.1)
3.
взвешенная
сумма ![]() ;
;
4.
взвешенное
среднее 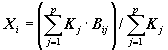 ;
;
где Bij
- компоненты j-го вектора, порождающего подмножества из p
исходных показателей, выраженные в нормированной шкале; Kj -
весовые коэффициенты, отражающие относительную важность j-го показателя
в конструкции обобщенного показателя. Множитель Kj
представляет собой произвольное положительное или отрицательное число,
задаваемое методами экспертных оценок. В состав порождающего подмножества могут
входить как исходные, так и ранее синтезированные обобщенные показатели.
Формулы являются взаимно приводимыми: например, если принять Kj
=1, то комплексный показатель, рассчитанный по формуле "взвешенная
сумма" будет равен простой сумме баллов исходных показателей.
В некоторых
случаях используется мультипликативная модель получения комплексного
показателя, например: ![]() , которая легко
сводится к аддитивной путем логарифмирования исходных
переменных.
, которая легко
сводится к аддитивной путем логарифмирования исходных
переменных.
Однако уместен
вопрос: насколько справедлива гипотеза аддитивности применительно к
экологическим показателям? По природе отображения предметной области
индивидуальные показатели могут быть отнесены к двум основным типам: экстенсивные,
или объемные, и интенсивные, или относительные.
Экстенсивные
показатели в свою очередь обычно имеют смысл запаса или потока.
Величины типа запаса регистрируются на конкретный момент времени и имеют
элементарные единицы измерения: экземпляр, тонна, джоуль, метр и т.д. Примерами
могут быть накопление гумуса в почве, количество аккумулированной энергии,
объем популяции или видовая плотность. Величины типа потока определяются только
за конкретный период времени и имеют размерность “объем в единицу времени”:
продукция в день или за вегетативный период, количество поступающей энергии в
час, количество изымаемых из экосистемы биологических ресурсов (например, вылов
рыбы) и т.д. Величины запаса и потока жестко связаны между собой:
Sь[v] + Pi
[v/t]t = Se[v] + Po
[v/t]t,
где Sь
и Se — запасы на начало и конец периода (v
— единица измерения), Pi и Р0 — потоки по увеличению и уменьшению
запаса (t — период). В частности, это соотношение лежит в основе
формирования таблиц материально-энергетического баланса. По нашему мнению, нет
никаких оснований для отклонения гипотезы аддитивности вкладов для экстенсивных
показателей. Действительно, использование простой суммы биомасс отдельных
составляющих сообществ дает общую биомассу живых организмов в водоеме,
взвешенная на ПДК сумма выбросов загрязняющих веществ в атмосферу достаточно
адекватно оценивает общий уровень ее загрязнения и т.д.
Интенсивные
показатели являются отношениями экстенсивных или интенсивных величин. Эти
индексы могут иметь разное содержание, разную размерность или быть безразмерными,
что определяется формулой их расчета. В подавляющем большинстве случаев для
получения относительных показателей пытаются "разделить одно на
другое": такие интенсивные величины размерности не имеют (т.е. выражаются
в долях, процентах, промилле и т.д.). К ним относятся темпы прироста,
коэффициенты пространственного сравнения, показатели ценозной и территориальной
структуры. Например, в экологии известны:
1.
индекс
Э.А.Пареле, как отношение численности тубифицид к численности олигохет в
водоеме;
2.
коэффициент
донной аккумуляции, как отношение концентраций вещества в донных отложениях и в
воде;
3.
коэффициент
видового сходства Т.Съеренсена, как отношение числа совпавших видов к общему
числу видов для двух сравниваемых фитоценологических проб;
4.
просто
коэффициент k2, как доля энергии, затраченной на
продуктивные процессы, от всей ассимилированной энергии.
Вряд ли можно
отрицать полезность и объективность относительных индексов, если их автор точно
знает, "что на что поделить", какие данные при этом использовать и
что сравнивать. Однако, как доказывает репрезентативная теория измерений, такие
показатели являются, как правило, неаддитивными и их агрегирование нельзя
проводить путем расчета средневзвешенных величин. Пусть, например, в некотором
регионе имеется аномально высокая смертность от какого-нибудь эпидемического
заболевания (скажем, атипичной пневмонии в размере 10%). Предположим, что в том
же регионе отсутствует смертность от некоторых других инфекционных заболеваний
(укуса мухи цеце, желтой тропической лихорадки и "коровьего
бешенства"). Нетрудно предположить, что комплексный показатель, равный
средней заболеваемости (2.5%), не будет адекватно отражать реальный уровень
эпидемиологической обстановки в регионе.
Можно привести
много других примеров того, как "осредняя" несколько исходных
показателей и превращая их в "интегральный" индекс, мы неизбежно
сводим все множество информационно насыщенных сигналов к некоторому
средневзвешенному узкополосному уровню ("обрезаем все неровности,
превращая мир данных в хорошо подстриженную лужайку"). Это особенно
характерно для оценки градаций экологического состояния изучаемого объекта по
всему имеющемуся множеству показателей. Для состояния, характеризуемого как
"экологическая катастрофа", вполне достаточно, чтобы всего лишь один
из анализируемых компонентов превысил летально опасный уровень загрязнения.
Если, например, все остальные показатели находятся на безопасном уровне
воздействия, то комплексный индекс, построенный с использованием гипотезы
аддитивности, вполне может оценить текущую экологическую обстановку как вполне
стабильную.
Другим возможным
вариантом синтеза комплексных показателей является метод оценки расстояния
до критического звена. Пусть, например, установлено, что на всем множестве
объектов (в случае ЭИС REGION - пространственно ограниченных участков
территории) имеется "наихудший эталон" – многомерная точка, для
которой по анализируемому набору исходных показателей имеют место наихудшие
значения, из всех встречающихся, с точки зрения благоприятности условий окружающей
среды. Тогда значение комплексного показателя для всех остальных точек может
быть интерпретировано как функция расстояния от данного объекта до выделенного
"наихудшего эталона". По совершенно аналогичному принципу может быть
определен "наилучший эталон" и найден вектор расстояний от каждой
точки до найденного экстремума. Если, например, использовать в качестве метрики
пространства расстояние по Евклиду, то будет подчеркнуто влияние отдельных
координат, имеющих аномально большие разности, поскольку они возводятся в
квадрат.
В общем случае
поиск "крайних точек" в многомерном пространстве является
нетривиальной оптимизационной задачей. Рассмотрим два эвристических алгоритма,
используемых в ЭИС REGION для расчета комплексных показателей с использованием
концепции расстояний. Внутреннее содержание этих алгоритмов основывается на том
обстоятельстве, что в ходе преобразования исходных показателей в нормированную
шкалу (см. раздел 3) учитывается их взаимосвязь с понятием "экологическое
состояние", т.е. для всех переменных при изменении их значений от 1 до 6
прогнозируется снижение качества окружающей среды.
Первый алгоритм
(процедура "Свертка") основан на использовании методов факторного
анализа. При этом все подмножество обобщаемых показателей свертывается к двум
главным компонентам и многомерное облако объектов
проецируется на факторную плоскость. Наихудшая критическая точка соответствует
участку, расположенному в верхнем правом углу двухмерной диаграммы факторных
оценок, а наилучшая краевая точка - в левом нижнем углу (см. рис. 17). Значение
комплексного показателя может быть определено, например, как взвешенное
расстояние от смещенного начала координат до каждой анализируемой точки:
![]() ;
;![]() (5.2)
(5.2)
где fi1
и fi2 - координаты i-го анализируемого региона в
пространстве двух главных компонент, f1min
и f2min - минимальные значения
соответствующих факторных оценок, l 1 и l 1 - значения собственных чисел.
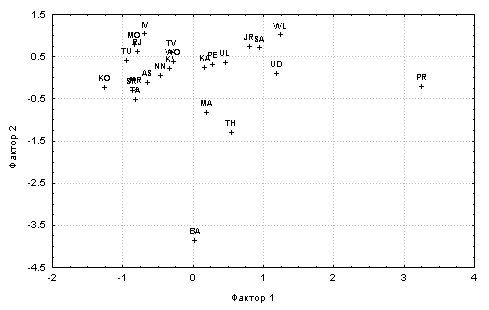
Рис.
17. Отображение территориальных единиц Волжского бассейна в пространстве двух главных
компонент после редукции 11 медико-статистических показателей (обозначения те
же, что и на рис. 8)
Второй алгоритм
(процедура "Оценивание") осуществляет выборку из базы данных по
каждому j-му обобщаемому показателю значений минимума Xmin и
максимума Xmax. Далее реализуется стандартная процедура
вычисления расстояний от каждого i-го участка до Xmin и Xmax
по евклидовой метрике:
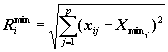 и
и 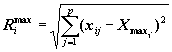 .
.
На основании этих
величин, а так же расстояния
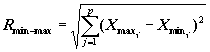 ,
,
осуществляется проецирование
координат каждого участка на отрезок [Xmin ¸ Xmax]:
![]() ;
;![]() (5.3)
(5.3)
Комплексные
показатели, полученные по любой из описанных трех процедур, подвергаются
стандартному преобразованию в нормированную шкалу, сохраняются в базе данных и,
наряду с другими индивидуальными показателями могут быть использованы в
дальнейшей обработке методами статистического моделирования или отображены на
картограмме.
Одной из важнейших
характеристик любых эколого-экономических моделей является вопрос их
адекватности. К сожалению, специфика предметной области не позволяет
использовать активный эксперимент и интерпретировать рассогласование модельных
и экспериментальных данных как признак неадекватности некоторых из принятых
аксиом. С другой стороны, для одного и того же эколого-экономического явления
или процесса можно, как правило, составить много возможных моделей или много
разновидностей одной базовой модели. Поэтому необходимы какие-то дополнительные
условия, которые позволяли бы из множества возможных моделей и математических
методов выбрать наиболее подходящие. В качестве одного из подобных условий
обычно выдвигается требование устойчивости метода анализа данных относительно
исходных допустимых отклонений, предпосылок модели или условий применимости
метода.
Предположим, как
это сделано в монографии [1], что имеются исходные данные, на основе которых
принимаются решения, а способ переработки (отображения) исходных данных в
решение назовем моделью. Таким образом, с общей точки зрения модель -
это функция, переводящая исходные данные в решение, причем конкретный способ
перехода особенного значения не имеет. Отметим, что в большинстве случаев
исследователей и практических работников, как правило, мало интересует тот
модельный формализм, который был использован при выработке решения. Вместе с
этим, очевидно, что предлагаемые решения формулируются в условиях неполноты
информации и допущений методов моделирования, поэтому более важны какие-то
заключения относительно устойчивости полученных моделей к этим допустимым
неопределенностям. Общая схема оценки чувствительности и устойчивости
статистических процедур подробно представлена в цитированной монографии.
Другим способом
повышения устойчивости решений является формирование коллектива
моделей-предикторов, эффективность которого практически всегда оказывается
значительно выше любого из его членов [2-4]. При этом очевидна аналогия с
методами коллективного решения, столь эффективно использующимися в обществе
[5-6]. Структурные связи в коллективе выбираются таким образом, чтобы
положительные свойства той или иной индивидуальной модели дополняли друг друга,
а отрицательные - компенсировались (т.е. срабатывал бы эффект системности типа
"целое больше суммы своих частей").
В разделе 4 мы
попытались на вербальном уровне оценить устойчивость различных разбиений
территориальных единиц Волжского бассейна на классы. Рассмотрим теперь на
конкретном примере устойчивость получаемых обобщенных показателей в зависимости
от конкретного алгоритма комплексации. Поскольку основной задачей разработанной
ЭИС является визуализация и анализ взаимной предупорядоченности участков
территории по сумме анализируемых переменных, абсолютные значения комплексных
показателей и характер их распределения важен нам лишь настолько, чтобы
обеспечить робастное отнесение точек к одним и тем же диапазонам (баллам)
стандартной нормировочной шкалы.
Выделим в базе
данных по Волжскому бассейну 11 медико-статистических показателей (общая
заболеваемость, канцерогенные новообразования, болезни системы кровообращения,
органов дыхания, пищеварения на 1000 чел. в 2001 г. и т.д.) и рассчитаем тремя различными алгоритмами
комплексный показатель уровня заболеваемости, обобщающий представленные данные
"одним числом":
а) По первому
алгоритму "Суммация" осуществим простое суммирование баллов
стандартной нормированной шкалы по формуле (5.1).
б) В соответствии
со вторым алгоритмом "Свертка" выполним редукцию 11 исходных
показателей к двум главным компонентам (см. рис. 16), которые в этом конкретном
случае объясняют свыше 64% имеющегося статистического разброса. Расчет
комплексных показателей проведем по формуле (5.2).
в) По третьему
алгоритму "Оценивание" обобщение индивидуальных показателей выполним
по формуле (5.3), определяющей положение каждой многомерной точки внутри
"минимаксного облака".
Для сопоставления
полученных результатов преобразуем рассчитанные комплексные индексы в
стандартную 6-балльную шкалу и определим для каждой территориальной единицы ее
ранги - порядковые номера в отсортированных списках, упорядоченных по
возрастанию результирующего показателя по каждой использованной версии (см.
таблицу 2)
Таблица 2
Значения
комплексных показателей, рассчитанных на основании обобщения 11
медико-статистических признаков тремя использованными алгоритмами (Балл -
значение показателя в стандартной нормированной шкале, СКО - сумма квадратов
отклонений от среднего балла)
|
Регион |
Алгоритм
"Суммация" |
Алгоритм
"Свертка" |
Алгоритм
"Оценивание" |
СКО |
|||
|
Балл |
Ранг |
Балл |
Ранг |
Балл |
Ранг |
||
|
Башкирия |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
Костромская |
1 |
2 |
1 |
4 |
1 |
3 |
0 |
|
Татарстан |
1 |
3 |
1 |
2 |
2 |
8 |
0.67 |
|
Саратовская |
1 |
4 |
1 |
3 |
2 |
6 |
0.67 |
|
Астраханская |
2 |
5 |
2 |
6 |
2 |
5 |
0 |
|
Тульская |
2 |
6 |
3 |
10 |
3 |
9 |
0.67 |
|
Мордовия |
2 |
7 |
2 |
5 |
1 |
4 |
0.67 |
|
Рязанская |
2 |
8 |
3 |
12 |
1 |
2 |
2 |
|
Нижегородская |
3 |
9 |
3 |
9 |
3 |
11 |
0 |
|
Московская |
3 |
10 |
4 |
14 |
3 |
12 |
0.67 |
|
Кировская |
3 |
11 |
3 |
11 |
2 |
7 |
0.67 |
|
Ивановская |
3 |
12 |
5 |
17 |
3 |
10 |
2.67 |
|
Волгоградская |
4 |
13 |
4 |
13 |
5 |
20 |
0.67 |
|
Тверская |
4 |
14 |
4 |
15 |
4 |
14 |
0 |
|
Марийская |
4 |
15 |
2 |
7 |
5 |
17 |
4.67 |
|
Калужская |
4 |
16 |
4 |
16 |
4 |
13 |
0 |
|
Чувашия |
5 |
17 |
2 |
8 |
4 |
15 |
4.67 |
|
Ульяновская |
5 |
18 |
5 |
19 |
5 |
18 |
0 |
|
Пензенская |
5 |
19 |
5 |
18 |
4 |
16 |
0.67 |
|
Ярославская |
5 |
20 |
5 |
20 |
6 |
23 |
0.67 |
|
Удмуртия |
6 |
21 |
6 |
21 |
6 |
21 |
0 |
|
Самарская |
6 |
22 |
6 |
22 |
5 |
19 |
0.67 |
|
Владимирская |
6 |
23 |
6 |
23 |
6 |
24 |
0 |
|
Пермская |
6 |
24 |
6 |
24 |
6 |
22 |
0 |
Представленные
результаты свидетельствуют о вполне очевидной устойчивости решений, мало
зависящих от типа алгоритма. Основываясь на использовании коэффициента
корреляции Спирмена, ранговые последовательности территориальных единиц,
сформированных разными методами, имеют высокий уровень сходства: от 0.8 между
алгоритмами 2 и 3 до 0.91 между алгоритмами 1 и 3. Нулевая гипотеза,
формулируемая как "нет корреляции между выборками", отклоняется с
высоким уровнем значимости. В 88% случаях рассчитанные комплексные показатели
либо полностью совпадают, или имеет место частный сдвиг в соседнюю градацию.
Литература
1.
Орлов А.И.
Устойчивость в социально-экономических моделях. - М.: Наука, 1979. - 296 с.
2.
Багров Н.А. О
комплексном методе прогнозов // Метеорология и гидрология. - 1962. - № 4. C.
14-21.
3.
Жуковский Е.Е., Брунова Т.И. Статистические методы оптимального
комплексования альтернативных прогнозов // Применение статистических методов в
метеорологии. - М.: Гидрометеоиздат, 1978. - C. 40-50.
4.
Розенберг Г.С., Шитиков В.К., Брусиловский П.М. Экологическое прогнозирование (Функциональные
предикторы временных рядов). – Тольятти: ИЭВБ РАН, 1994а. – 182 с.
5.
Растригин Л.А., Эренштейн Р.Х. Метод коллективного распознавания. – М.: Энергоатомиздат, 1981. – 80
с.
6.
Льюс
Р.Д., Райфа Х. Игры и решения.
- М,: Изд-во иностр. лит., 1961. - 642 с.
6.
Моделирование причинно-следственных связей
Важной задачей ЭИС в построении прогнозов
изменения состояния экосистемы или изменения "качества" окружающей
среды в рамках отдельного региона является анализ причинно-следственных связей
между индивидуальными и комплексными показателями.
Любая эколого-экономическая система
представляет собой большой, сложный, слабо детерминированный и эволюционирующий
объект исследования. Теория самоорганизации моделей показывает, что этот
объект, как и огромное большинство других процессов в природе, может быть
описан, например, в виде полиномов высокой степени, являющихся частным случаем
обобщенного полинома Колмогорова – Габора [1]:
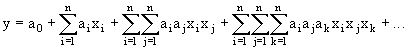 ;
;![]() (5.1)
(5.1)
Число членов полного полинома равно ![]() , где m – число
переменных, q – степень полинома, и уже при n=q=7
достигает 3600. Поэтому основная задача моделирования сложных систем на основе
структурных уравнений причинно-следственной связи заключается в том, чтобы
исключить в полиноме (5.1) подмножество “лишних” неинформативных коэффициентов
и сохранить необходимое и достаточное сочетание объясняющих членов. Сложность
синтезированной модели будет оптимальной, если необходимая адекватность обеспечивается
при минимальном количестве составляющих ее элементов [2].
, где m – число
переменных, q – степень полинома, и уже при n=q=7
достигает 3600. Поэтому основная задача моделирования сложных систем на основе
структурных уравнений причинно-следственной связи заключается в том, чтобы
исключить в полиноме (5.1) подмножество “лишних” неинформативных коэффициентов
и сохранить необходимое и достаточное сочетание объясняющих членов. Сложность
синтезированной модели будет оптимальной, если необходимая адекватность обеспечивается
при минимальном количестве составляющих ее элементов [2].
Как и в других подсистемах экспертной системы
ЭИС REGION блок "Моделирование связей" также предоставляет широкие
возможности для построения статистических моделей разного типа и уровня сложности
на основе укомплектованной библиотеки методов и алгоритмов.
Модель множественной регрессии
Наиболее простым, но весьма эффективным
методом идентификации причинно-следственных отношений является построение
модели множественной линейной регрессии:
![]() ;
;![]() (5.2)
(5.2)
где p - количество
показателей-регрессоров, n - количество измерений; xij
-совокупность варьируемых переменных, определяющих факторы воздействия на
исследуемый объект (i = 1,n, j = 1,p), Yi
- параметр состояния i-го объекта (отклик), e - погрешности, искажающие зависимость (независимые случайные
величины).
Метод обеспечивает получение компактных и
легко интерпретируемых уравнений связи, которые легко могут быть использованы
для объяснения. При соблюдении известных исходных предпосылок метод
предоставляет также развитый статистический аппарат исследования значимости
полученной модели и оценки ее адекватности. В меньшей степени уравнения этого
типа целесообразно использовать для прогнозирования - расчета ожидаемых
значений отклика Y, поскольку в этом отношении они могут уступать
моделям МГУА и нейросетевым моделям.
Стандартная процедура линейного
множественного регрессионного анализа заключается в определении количественного
изменения функции отклика от нескольких причин-факторов и построении такого
уравнения плоскости в (p+1)-мерном пространстве, отклонения результатов
наблюдений Yi от которой были бы минимальными. То есть,
следует вычислить параметры - значения коэффициентов b0, bj
в линейном уравнении ![]() , что равносильно минимизации
выражения
, что равносильно минимизации
выражения
![]() ® min ,
® min ,
где ![]() -
расчетные значения исследуемой характеристики i-го объекта. Для отыскания этого
минимума необходимо найти частные производные по всем неизвестным b0,
b1,…, bp и приравнять их нулю. Полученные
уравнения образуют систему нормальных уравнений:
-
расчетные значения исследуемой характеристики i-го объекта. Для отыскания этого
минимума необходимо найти частные производные по всем неизвестным b0,
b1,…, bp и приравнять их нулю. Полученные
уравнения образуют систему нормальных уравнений:
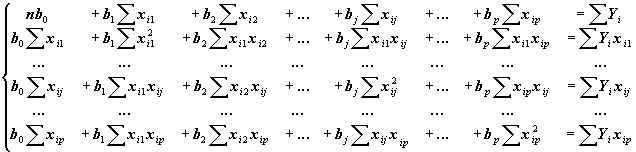
Для решения полученной системы используются
стандартные методы линейной алгебры (в нашем случае - метод Гаусса с выбором
главного элемента по всей матрице).
Отклонение отдельной точки от плоскости регрессии
называется остатком. Чем меньше разброс значений остатков к общему разбросу
значений, тем лучше построенная линия характеризует связь Y
от переменных Х. Индикатором степени подгонки модели к данным служит
коэффициент детерминации (R2), значение которого изменяется
от 0 до 1. Чем ближе значение R2 к единице, тем больший
процент остаточной изменчивости может быть объяснен и тем точнее построена
модель.
В общем случае исходные показатели вносят
различный вклад в объяснение и прогнозирование анализируемого отклика и могут
быть разбиты на две категории: информативные переменные, существенные для
решения поставленной задачи, и незначимые переменные, несущие мало
дополнительной информации для нахождения искомой зависимости. Поэтому основной
задачей регрессионного анализа является включить в уравнение (5.2) только то
минимальное подмножество входных информативных переменных x,
которое без существенной потери информации позволяет объяснить имеющийся
статистический разброс. Отбор таких переменных в традиционной регрессии
осуществляют с использованием различных секвенциальных (последовательных)
процедур, осуществляющих "взвешивание" признаков с использованием
различных статистических критериев. В итоге с заданной надежностью из полной
матрицы стандартизированных нормальных уравнений выбирается наилучшая
невырожденная подматрица, т.е. формируется модель наиболее оптимальной
структуры. Выполнение этих процедур в ЭИС REGION осуществляется с
использованием двух специализированных программных модулей, реализующих методы И.Я.
Лиепы [3] и М.А. Эфроимсона [4-5].
Исключение несущественно влияющих факторов по
методу Лиепы осуществляется следующим образом. Определяются показатели
удельного веса влияния факторов Xj :
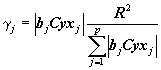 ,
,
где R - коэффициент множественной
корреляции, Сyxj -
коэффициент ковариации между Y и фактором Xj.
![]() ,
,
где Q - общая сумма квадратов
отклонений значений отклика от арифметического среднего:
![]() ;
;
Qz - сумма
квадратов отклонений эмпирических значений Y от гиперплоскости регрессии:
![]() ;
;
коэффициенты ковариации определяются по
формуле:
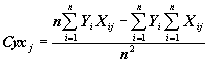 .
.
Достоверность показателя удельного веса
(γj) вычисляется по формуле:
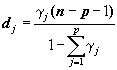
и проверяется по критерию Фишера со степенями
свободы v1 = 1, v2 = n - p -
1. Если p-значение, соответствующее Fф(dj,
v1, v2) ,больше pcrit, то
воздействие фактора считается несущественным и такой фактор из процедуры
вычислений исключается. На следующем шаге вычислений пересчитываются
коэффициенты bj в пространстве оставшихся факторов. Процесс
останавливается, когда останутся только существенные факторы.
В отличие от метода Лиепы, стандартная
пошаговая процедура Эфроимсона осуществляет как последовательное включение
переменных в модель, так и исключение незначимых факторов. При этом
используется традиционная статистика – t-критерий для проверки
равенства нулю частного коэффициента корреляции. Квадрат этого критерия имеет F-распределение
и поэтому называется последовательным (или частным) F-критерием Фишера
для включения (либо исключения).
Выбор первой переменной для включения в
модель осуществляется для признака xl, который имеет
наибольший по абсолютной величине коэффициент парной корреляции с откликом rql.
При этом процедура включения выполняется, если справедливо неравенство для последовательного F-критерия: F
> Fo, где Fo – заранее
заданное исследователем пороговое значение. Процесс расширения количества
переменных модели повторяется многократно, пока статистическая значимость
включения очередного признака по F-критерию на каждом шаге
превышает заданный порог Fо.
После очередного расширения модели анализируется взаимная коррелированность
отобранных переменных и, если их взаимосвязь существенна, то лишние факторы,
вносящие наименьший вклад, из модели исключаются. Более точно, исключению
подлежат те переменные, для которых вычисленное значение частного F-критерия
меньше Fо.
Вычисления прекращаются, если не осталось ни одной переменной, для которой
вычисленное значение последовательного F-критерия превысило бы
заданный порог.
Недостатком классического регрессионного
метода является априорное предположение о линейности связи. Поскольку для
описания сложно организованных систем необходим учет нелинейности связей,
пространство исходных аргументов искусственно расширяется за счет включения псевдо-переменных, полученных в результате нелинейного
преобразования базисных показателей. Кроме натуральных степеней исходных
переменных и различных их алгебраических комбинаций можно использовать и другие
функции от них: lnX, ![]() , 1/X
, e a X,
тригонометрические преобразования,
логистическую функцию 1/(1+e–X),
преобразование Бокса-Кокса
, 1/X
, e a X,
тригонометрические преобразования,
логистическую функцию 1/(1+e–X),
преобразование Бокса-Кокса ![]() и т.д.
и т.д.
Рассмотрим в качестве примера моделирования
причинно-следственных связей структурно-функциональную идентификацию
зависимости между комплексным показателем заболеваемости населения (отклик) и
11 индивидуальными показателями, представленными в разделе 3 и использованными
в примере кластерного анализа (показатели M_OZ, M_OD, M_RK и M_DS по понятным
причинам из списка варьируемых переменных были исключены).
Полученное полное уравнение множественной
линейной регрессии (5.2), включающее все влияющие факторы, является в целом
информационно незначимым по критерию Фишера - F(11,12)= 1.42, p= 0.27. Из всех
11 коэффициентов при объясняющих переменных статистически значимыми по критерию
Стьюдента оказались только 2, учитывающие производство электроэнергии (E_PE) и
выбросы в атмосферу от автотранспорта (Z_AA). Коэффициент множественной
корреляции фактических и расчетных значений r = 0.075.
Процедура исключения незначимых переменных
методом И.Я.Лиепы приводит к информационно значимому компактному уравнению,
выражающему обратно пропорциальную зависимость заболеваемости населения от двух
перечисленных показателей:
Y = 0.797 - 21.031 E_PE - 2.23 Z_AA , (r
= 0. 289).
Уместно заметить, что сам факт исключения
переменной из числа регрессоров часто совсем не означает отсутствие реального
влияния отброшенного признака на анализируемый показатель. Метод И.Я.Лиепы
старается включить в уравнение статистически независимые члены, а в случае их
взаимной коррелированности - только один из связанного комплекса показателей.
Например, объем производство электроэнергии хотя и косвенно, но более адекватно
отражает и объем выбросов в атмосферу ТЭЦ и степень
техногенной деградации территории.
Для учета нелинейных взаимодействий дополним
исходную матрицу различными математическими функциями от 11 исходных
показателей. Число переменных после преобразования становится равным 47. В
расширенном пространстве признаков реализуем процедуру включений с исключениями
Эфроимсона при пороге включения Fo = 3.5 и получим следующее уравнение
регрессии:
Y = 0.897 -3.27599 ![]() -
2.17 Z_AA,
-
2.17 Z_AA,
которое является информационно значимым (F =
4.63) и существенно превосходит линейную модель по своим статистическим
характеристикам (r = 0.553, стандартное отклонение для остатков s = 0.224).
При снижении порога включения по частному
критерию Фишера до Fo = 2.7 можно получить более точную модель:
Y = 2.16 - 3.57 ![]() - 1.19
- 1.19 ![]() + 0.135 E_VP - 0.00742 C_MU
- 19.14 Z_AA + 8.98
+ 0.135 E_VP - 0.00742 C_MU
- 19.14 Z_AA + 8.98 ![]() - 9.645/Z_SV + 0.242
- 9.645/Z_SV + 0.242 ![]() + 0.0031 Z_KP ,
+ 0.0031 Z_KP ,
учитывающую дополнительный комплекс исходных
показателей - валовый региональный продукт (E_VP), внесение минеральных
удобрений (C_MU), образование токсичных отходов (Z_TO), сброс
сточных вод (Z_SV), долю проб воды, не отвечающих нормативам (Z_KP), и
выполняющую более точную аппроксимацию данных (F = 7.65, r = 0
.91, s = 0 .135).
Модели на основе самоорганизации
Математическое моделирование основано на двух
возможных подходах:
1. традиционном дедуктивном, идущим "от общих закономерностей
функционирования объекта - к конкретной математической модели";
2. индуктивном, идущим "от конкретных данных наблюдений - к
общей модели", т.е. исследователь предоставляет выборку, выдвигает
гипотезу о возможном классе моделей и задает критерий выбора наилучшей модели в
этом классе, после чего за дело принимается компьютер.
Задача исследования причинно-следственных
связей между факторами эколого-экономической системы и восстановления частных
статистических зависимостей по эмпирическим данным решается, как правило, с
использованием индуктивного пути, поскольку какие-либо априорные предположения
о характере внутрисистемных взаимодействий отсутствуют. Однако все индуктивные
методы отличаются тем, что в них общие выводы делаются на основании частных
фактов, а это может привести как к верным, так и к ошибочным решениям. Причина
такой неопределенности состоит в том, что частные факты, на которых
основываются общие выводы, не всегда хорошо характеризуют изучаемое явление.
Вместе с тем, получаемые общие выводы должны объяснять не только частные факты,
но и все изучаемое явление целиком, т.е. общие выводы не должны изменяться при
практически бесконечном расширении числа экспериментов. Поэтому качество
индуктивного вывода должно определяться не только и не столько объяснением
отдельных, полученных в процессе экспериментов фактов, сколько от
экстраполяционных способностей этих выводов, их способностью к экспансии в
область явления, не охваченную экспериментом.
В задачах восстановления многомерных
зависимостей ограниченность информации накладывает допустимые пределы сложности
модели. Чем больше фактов, тем выше может быть предельная сложность
синтезируемой модели и, наоборот, чем беднее фактический материал, тем беднее
по сложности может быть построенная модель. Чем сложнее модель, тем больше у
нее возможностей в объяснении ограниченного числа экспериментальных фактов
(упрощения приводят к сглаживанию важных деталей). Но, всякий раз, когда модель
выбирается из слишком сложного класса, все в большей мере не хватает
эмпирических данных для ее однозначного объяснения (факты просто не в состоянии
воссоздать такую модель и последняя начинает вести себя причудливо в области,
не охваченной экспериментом). Т.к. объем выборок всегда ограничен, неизбежно
возникает центральная проблема всех индуктивных методов, состоящая в правильном
соотношении сложности аппроксимирующей функции (т.е. сложности модели) с
объемом исходных данных для обучения.
С конца 60-х годов усилиями украинских
кибернетиков [1] были обозначены основные принципы самоорганизации моделей,
которые легли в основе нового направления в математическом анализе данных,
известном как метод группового учёта аргументов – МГУА (Group Method of Data
Handling, GMDH). Основной особенностью алгоритмов МГУА явилось то, что для непрерывных зашумленных данных, метод выбирает оптимальную
упрощенную нефизическую модель. Модели самоорганизации МГУА можно рассматривать
как своеобразное связующее звено, объединяющее различные методологические
концепции, представленные как классической параметрической статистикой, так и
современными методами искусственного интеллекта.
Отличие алгоритмов МГУА от других алгоритмов
структурной идентификации и селекции лучшей регрессии состоит в следующих
свойствах:
1.
Эвристический
характер выбора главного критерия и ограничений, лежащих в основе
переборной процедуры: в качестве ведущего критерия селекции могут быть
использованы различные известные критерии (оценки
"скользящего контроля" PRR(s), регулярности AR(s) и баланса
переменных BL(s) и т.д.);
2.
Большое разнообразие
генераторов структур многорядного характера: применяются оригинальные
итерационные процедуры полного или сокращенного перебора вариантов структур
модели;
3.
Свобода выбора: в
многорядных алгоритмах МГУА с одного уровня многорядной модели на следующий
передаются не один, а несколько лучших результатов;
4.
Внешнее дополнение:
исходная выборка делится на части для построения и оценки модели, при этом
критерии селекции моделей рассчитываются на новой независимой информации;
5.
Робастность
подхода: автоматическая
адаптация сложности оптимальной модели и внешних критериев к уровню помех в
системе.
С одной стороны, МГУА считается, своего рода,
интеллектуальным обобщением регрессионного анализа, понимаемого в наиболее
широком смысле. От классической множественной регрессии МГУА отличается лишь
использованием специфических квадратичных критериев внешнего или внутреннего
типа, а также многорядными итерационными процедурами нахождения оптимального
решения задачи. С другой стороны, процедуры МГУА имеют все признаки
эволюционного алгоритма – отбор (селекция) и генерация нового поколения.
Рассмотрим процесс синтеза модели оптимальной
сложности более подробно. Представим функцию, аппроксимирующую набор исходных
данных, в общем виде: y = F(x1,
…, xm). Выше упоминалось, что такой функцией может быть
полином Колмогорова-Габора (5.1), с помощью которого можно добиться весьма
точной аппрокимации любой дифференцируемой функции. Заменим эту сложную
зависимость множеством частных описаний, т.е. простых функций, аргументами
которых является произвольная пара исходных аргументов:
y1 = f(x1,
x2) ; y2 = f(x1, x3)
; ys = f(xm-1, xm);
где s=C2m, причем вид
функции f одинаков для всех пар в течение всего процесса обучения. Очень
часто в качестве функции f выбираются простые зависимости
y(xi, xj) = a0
+ a1xi + a2xj
+ a3xixj
или y(xi, xj) = a0
+ a1xi + a2xj
+ a3xixj + a4xi2
+ a5xj2.
Предварительно вся выборка разделяется на две
части: обучающую и проверочную. Тем самым порождается внешнее дополнение
(проверочная выборка), которая играет роль сита, отсеивающего все чрезмерно
сложные модели, не имеющие права на существование в рамках ограниченной
информации. Коэффициенты a0 – a5 частных
описаний определяются по данным обучающей выборки. В результате комбинаторики
возможных пар из m исходных аргументов получается множество решений,
поскольку частное уравнение каждой пары рассматривается как некоторая
упрощенная модель восстанавливаемой функции. Из полученного набора упрощенных
моделей первого ряда отбирается часть, например, s* в
некотором смысле наилучших, показавших хорошие результаты на проверочной
выборке, не участвовавшей в определении коэффициентов уравнений (т.е. на
внешнем дополнении).
Далее вступает в действие принцип
неокончательности решений: ни одна из полученных на первом этапе моделей не
принимается за истину и наращивание сложности модели продолжается. Прошедшие
самоотбор частные описания формируют множество новых переменных, которые
являются исходными аргументами для частных описаний 2-го ряда:
z1 = f(y1, y2)
; z2 = f(y1, y3) ; zs
= f(ys-1, ys).
Коэффициенты новых
моделей находятся по МНК на точках той же обучающей последовательности. Новые
модели проверяются на точках проверочной последовательности, и среди них
выбирается s* наилучших, которые используются в качестве аргументов
следующего третьего ряда и т.д.
Сложность общей
модели возрастает от ряда к ряду. Так, например, во втором ряду появляются
нелинейные члены вида (x1x3), (x12x3),
(x12x2 x3) и
т.д. Алгоритм останавливается сразу же по достижении единственного минимума
отклонений, полученных на проверочной выборке. Количество pядов
селекции обычно рекомендуется наpащивать до s = (m - 1),
хотя в литеpатуpе описан случай, когда самая несмещенная линейная модель в
пpимеpе с 5 аpгументами получилась на 30-м pяду селекции. На пpактике усложнение модели пpекpащают, когда дальнейшее
улучшение кpитеpия селекции не будет пpевышать некотоpого числа e (паpаметp алгоpитма). Тем самым выбирается модель оптимальной
сложности, устанавливающая компромисс между сложностью и опасностью
“переобучения”.
В ЭИС REGION
используется авторский модуль, реализующий общую схему многорядного алгоритма
МГУА с частными описаниями в виде нелинейной функции двух переменных. Поскольку
пpи использовании нелинейных опоpных функций
отмечается опасность потеpи существенного аpгумента, то была использована
модификация алгоpитма, оптимизиpующего на каждом шагу длину частного описания
(напpимеp, выбиpающая вид частного описания с максимумом коэффициента
коppеляции на пpовеpочной последовательности [6]).
Реализуем алгоритм
МГУА на тех же исходных данных, что и при построении моделей множественной
регрессии. Наилучшая модель МГУА для прогноза заболеваемости населения (Y) пpи 11 исходных аpгументах была получена на 6-м pяду
селекции, когда был найден максимум коэффициента коppеляции Kкор
= 0.983 на примерах пpовеpочной последовательности. Oптимальная модель (М6) имела вид:
Y = -0.00352 + 0.702 u1 +
0.304 u2,
где промежуточные переменные u1
и u2 могут быть вычислены по частным описаниям 5-го
ряда селекции:
u1 = 0.0517 - 0.663 v1 + 1.567 v7
,
u2 = 0.0304 - 0.639 v2 +
1.589 v7 .
Аналогичный вид имеют частные описания на остальных
промежуточных рядах селекции:
|
4-м ряду: |
v1 = - 0.00579 + 0.037 z1
+0.974 z2; |
|
v2 = 0.144 - 0.0768 z2 -
0.057 z4 + 1.485 z2× z4; |
|
|
v7 = 0.184 + 1.256 z7 - 1.5 z8
- 0.489 z7× z8 + 1.97 z82;
|
|
|
3-м ряду: |
z1 = - 0.027 + 0.546 y1 +
0.505 y7; |
|
z2 = 0.0726 + 0.02 y2 + 0.161
y8 + 1.187 y2× y7; |
|
|
z4 = - 0.047 + 0.56 y4 +
0.523 y2 ; |
|
|
z7 = - 0.048 + 0.304 y7 +
0.786 y2 ; |
|
|
z8 = 0.204 - 0.186 y8 - 0. 49
y4 + 2.275 y8× y4 ; |
|
|
2-м ряду: |
y1 = - 0.0526 + 0. 195 x1 +
0. 903 x5 ; |
|
y2 = - 0.0297 + 0. 215 x2 +
0.41 x5 + 0.775 x2 × x5 ; |
|
|
y4 = - 0. 303 + 0. 761 x4 +
10.804 x7 ; |
|
|
y7 = x6 ; |
|
|
y8 = 0.00185 + 0.299 x8 + 0.
108 x5 + 1.046 x8 × x5 . |
И, наконец, на 1-м ряду селекции появляются
исходные переменные:
x1 = 0.596 + 0.00561 (E_VP) - 2.589 (Z_AA) ;
x2 = 0.797 - 21.03 (E_PE) - 2.23 (Z_AA);
x4 = - 0.145 + 0.0726 (C_MU) + 0.00945 (Z_SV) -
0.00276 (C_MU) (Z_SV) ;
x5 = 0.696 - 0.00595 (Z_SV) + 0.453 (Z_AA) + 0.191
(Z_SV) (Z_AA) - 41.35 (Z_AA)2 ;
x6 = 0.397 - 0.00063 (Z_KP) + 4.1 (Z_AA) + 0.373
(Z_KP) (Z_AA) - 39.54 (Z_AA)2 ;
x7 = 0.3012 + 17.9 (Z_AA) - 371.92 (Z_AA)2
;
x8 =.0.479 + 0.983 (Z_TO) + 0.905 (Z_AA) - 41.29
(Z_TO) (Z_AA) + 0.074 (Z_TO)
По 6-рядной модели самоорганизации трудно
судить, какой конкретно вклад вносит каждая из исходных переменных. Можно лишь
констатировать их наличие (или встречаемость) в частных описаниях с помощью
следующей структурной таблицы, обозначившей приоритетное влияние на здоровье
населения выбросов от автомобильного транспорта:
|
Наименование |
Шифр |
Встречаемость |
|
Валовый региональный продукт, млн.руб./чел. |
E_VP |
1 |
|
Производство электроэнергии, млн.кВт в час/чел. |
E_PE |
1 |
|
Внесение минеральных удобрений, кг/га |
C_MU |
1 |
|
Сброс загрязненных сточных вод, куб.м/чел. |
Z_SV |
2 |
|
Удельный вес проб, не отвечающих
гигиеническим нормативам по санитарно-токсикологическим показателям |
Z_KP |
1 |
|
Суммарные выбросы в атмосферу загрязняющих
веществ, т/чел. |
Z_VA |
1 |
|
Выбросы в атмосферу от автомобильного транспорта,
т/чел. |
Z_AA |
6 |
|
Образование токсичных отходов, т/чел. |
Z_TO |
1 |
Представленная форма многорядного
представления моделей МГУА, где в каждом слое локализуются достаточно простые функции
(полиномы не более 2 порядка от двух переменных), но зато общая целостная
модель представляет чрезвычайно сложную конструкцию, содержит много общего с
моделями искусственных нейронных сетей.
Основу нейронных сетей также составляют относительно
простые элементы (ячейки), имитирующие, по замыслу авторов, работу нейронов
мозга. На вход каждого нейрона - см. рис. 18 - подается группа из n
сигналов (синапсов), которые преобразуются по заданному алгоритму в
выходной сигнал (аксон).
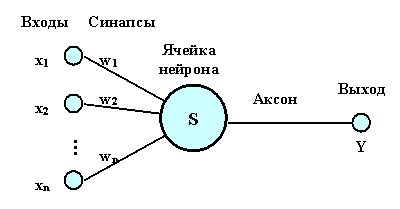
Рис.
18. Схема работы нейрона
Алгоритм преобразования сигналов в нейроне
достаточно прост:
![]() ,
,
где T - постоянная (порог нейрона); wi
- настраиваемые коэффициенты при входных сигналах (веса синапсов) , f
-функция активации, которая имеет вид несложного математического выражения
(линейного, сигмоидного, логарифмического, степенного и т.д.), выбираемого в
зависимости от характера решаемых задач.
Нейроны организуются в слои - рис. 19.
Входной слой служит для ввода значений переменных. Каждый следующий слой
связывается с предыдущим. Выходной слой отвечает за работу всей нейронной сети.
Выбор конкретной архитектуры сети (числа слоев и количества нейронов в каждом
из них) также зависит от поставленной задачи. Наиболее популярны многослойные
персептроны (MLP - Multy Layer Perceptron) или нейронные сети прямого
распространения, которые и являются основным предметом нашего рассмотрения.
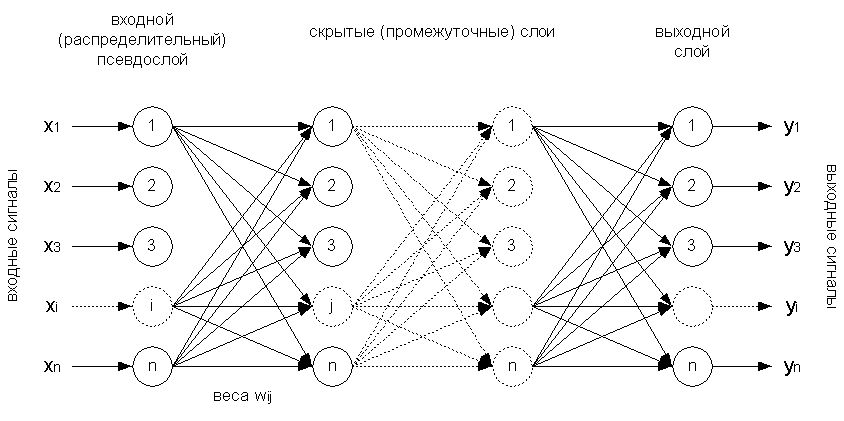
Рис.
19. Структура многослойного персептрона
Выходные сигналы в нейронной сети комбинируют
друг с другом по правилам суперпозиции, т.е. для каждого узла при движении от
входа сети к ее выходу последовательно выполняется преобразование линейных
комбинаций входов в соответствии видом принятой функции активации.
Результирующее значение функции отклика снимается с выходного слоя.
Представляет интерес выделить основные
сходные черты и отличия методов самоорганизации (МГУА) и нейросетевого
моделирования:
1.
теоретическое
обоснование обоих методов базируется на теореме Колмогорова, доказавшего, что
любую непрерывную многомерную функцию можно представить в виде конечного числа
простых одномерных функций [7];
2.
в
соответствии с "коннекционистской" парадигмой и тут и там модель
реализуется в виде многорядной структуры персептрона, конечное решение которого
доставляется с последнего слоя;
3.
в
обоих случаях, как средство профилактики от "переобучения"
используется внешнее дополнение в виде проверочной выборки;
4.
если
в МГУА входом в каждый узел является два и только два сигнала, приводящих к
локально наилучшему результату, то в нейрокомпьютинге входами являются все
аксоны предыдущего слоя, степень активности которых регулируется значениями
весов wi;
5.
в
качестве функции активации нейронов модно использование сигмоидной функции ![]() , когда как в МГУА в
моде уравнение параболоида;
, когда как в МГУА в
моде уравнение параболоида;
6.
МГУА
автоматически воспроизводит схему массовой селекции, которая аналогична задаче
нахождения пеpцептpона оптимальной структуры, в то
время как архитектура тестируемой сети, как правило, заранее задается
исследователем (впрочем, есть работы по методам многослойной самоорганизации
нейронных сетей оптимальной сложности [8]);
7.
если
в МГУА реализовано последовательное обучение, оптимальное только с точки зрения
данного конкретного шага, то настройка параметров нейронной сети происходит в
ходе итеративной процедуры, минимизирующей совокупную ошибку всей сети целиком;
8.
нейрокомпьютинг
перегружен чисто "анатомической" лексикой, проводящей сомнительную по сути и рекламную по характеру аналогию с
работой человеческого мозга, чего счастливо избежал МГУА.
Расширенные концепции
нейросетевого моделирования, описание архитектуры и особенностей различных
типов сетей, алгоритмы обучения и прочие важные темы для обсуждения читатель
может найти на многочисленных сайтах Интернет, что дает нам возможность
прекратить дальнейшие теоретические упражнения.
Интеллектуальным расширением ЭИС REGION в
области использования эволюционных алгоритмов и методов нейросетевого
моделирования является информационный интерфейс с универсальной программой
нейросетевого анализа STATISTICA Neural Networks [9]. Это дает возможность
эффективно решать задачи регрессии с помощью сетей различных типов:
многослойного персептрона, линейной сети, радиальной базисной функции и
обобщенной регрессионной сети.
Выполним теперь анализ связи между уровнем
заболеваемости и прочими факторами с использованием искусственных нейронных
сетей. Особенностью нейросетевого моделирования является разделение исходной
матрицы данных на две части: обучающую выборку и проверочную
последовательность. Проведем тестирование с помощью инструмента Network Advisor
40 возможных сетей-претендентов и найдем версию сети с наилучшей конфигурацией
- трехслойный персептрон с 6 нейронами в промежуточном слое и сигмоидной
функцией активации (см. рис. 20), обеспечивающую минимальную ошибку
предсказания на проверочной последовательности, включающей 7 векторов из 24.
Точность аппроксимации данных с помощью нейронной сети существенно превосходит
результаты, полученные регрессионными моделями: для обучающей выборки r
= 0.987, s = 0.049, для проверочной последовательности r = 0.85, s
= 0.106.
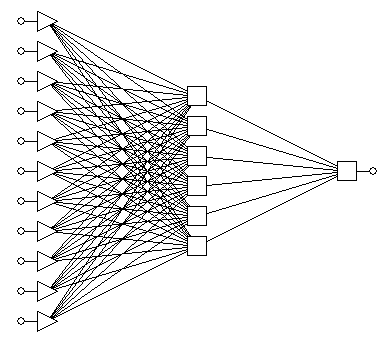
Рис.
20. Вид трехслойного персептрона, реализующего прогнозирование уровня
заболеваемости от 11 эколого-экономических показателей
Пошаговые
процедуры Лиепы и Эфроимсона, формирующие набор информативных признаков, не
всегда приводят к результату, достаточно близкому к
оптимальному. Эффективный автоматизированный подход к выбору значимых входных
переменных реализуется с использованием генетического алгоритма, который
можно считать “интеллектуальной” формой метода проб и ошибок. Генетический
алгоритм [10, 11], позаимствованный у природных аналогов, является наиболее
ярким представителем эволюционных методов и представляет собой мощное поисковое
средство, основанное на трех компонентах:
1.
генетической
памяти, сконцентрированной в “хромосомах”;
2.
воспроизведения,
осуществляемого при помощи операторов кроссинговера и мутации;
3.
селекции
продуктивных решений методами оптимизации многоэкстремальных функций.
На рассматриваемом
примере процесс эволюции продолжали на протяжении 100 поколений, т.е. цикл
“отбор-порождение-оценка” был повторен 100 раз и при этом в
поисках оптимального набора генов было построено и оценено 10000 версий
нейросетевых моделей. В соответствии с найденным
субоптимальным решением были выделены три наиболее значимых исходных
показателя: затраты на природоохранные мероприятия (E_ZP), внесение пестицидов
(C_SP) и сброс загрязненных сточных вод (Z_SV), список которых далеко не
совпадает с наборами, полученными секвенциальными методами. Наилучшая
сеть - трехслойный персептрон, ограниченный тремя входами (см. рис. 21), также
показал вполне удовлетворительные результаты на проверочной последовательности:
r = 0.81, s = 0.085, что свидетельствует о хороших
экстраполяционных свойствах модели.
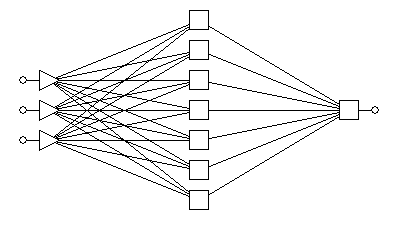
Рис.21.
Трехслойный персептрон с тремя входами, реализующий прогнозирование уровня
заболеваемости от набора наиболее информативных показателей
Литература
1.
Ивахненко А.Г., Зайченко Ю.П., Димитров В.Д. Принятие решений на основе самоорганизации. – М.: Сов. радио, 1976. – 280 с.
2.
Эшби У.Р. Введение в
кибернетику. – М.: Ин. литер., 1959. – 432 c.
3.
Лиепа И.Я. Показатель
удельного веса влияния факторов воздействия // Уч. зап. Латв. ун-та. Рига:
Изд-во ЛатвГУ, 1971. С. 36-40.
4.
Efroimson M.A. Multiple
regression analysis // Mathematical Methods for Digital Computers. 1960. V. 1. P. 191-203.
5.
Дрейпер
Н., Смит Г. Прикладной
регрессионный анализ: В 2-х кн.– М.: Финансы и статистика. Кн. 1. 1986. – 366
с.; Кн. 2. 1987. – 351 с.
6.
Справочник
по типовым программам моделирования / Под ред.
А.Г.Ивахненко - Киев: Техника,1980. - 184 с.
7.
Головко В.А.
Нейроинтеллект: Теория и применения. Книга 1 Организация и обучение нейронных
сетей с прямыми и обратными связями. – Брест: БПИ, 1999. – 260 с. Книга 2 Самоорганизация,
отказоустойчивость и применение нейронных сетей – Брест: БПИ, 1999. – 228 с.
8.
Щетинин В.Г.
Многослойная самоорганизация нейронных сетей оптимальной сложности// Автоматика
и вычислительная техника. - Рига, 1998. - №4. - С.30-37.
9.
Нейронные сети.
Statistica Neural Networks. – М.: Горячая линия – Телеком, 2001. – 182 с.
10.
Скурихин А.Н.
Генетические алгоритмы // Новости искусственного интеллекта. 1995. № 4. С.
6-46.
11. Васильев В.И., Ильясов Б.Г. Интеллектуальные системы управления с использованием
генетических алгоритмов. Учебное пособие. – Уфа: УГАТУ, 1999. – 105 с
Территория
Волжского бассейна – это 1360 тыс. км2
(62,2% европейской части России или почти 13% территории всей Европы)
включающая 40 административных единиц (областей и автономий; две из них – в
Казахстане, остальные – в России; в ЭИС REGION представлены 24 административные
единицы России, которые охватывают более чем 90% всей территории Волжского
бассейна). В своем движении от истоков к устью крупнейшая
река Европы пересекает лесную (до гг. Нижний Новгород и Казань), лесостепную
(гг. Самара и Саратов), степную (до г. Волгограда) и полупустынную зоны.
Промышленность и сельское хозяйство в Волжском бассейне дают почти третью часть
всей продукции России и, соответственно, пропорционально этому велика
антропогенная нагрузка на регион. Все это делает регион Волжского бассейна
одним из наиболее напряженных по экологической обстановке
[1-3].
В рамках
эколого-информационной системы REGION изучаемая территория разбита на 210
участков, по которым в базе данных было оцифровано более 500 показателей.
Комплексный анализ имеющейся информации с помощью модулей экспертной системы
позволяет оценить экологическое состояние Волжского бассейна по
эколого-экономическим и социальным показателям.
Обобщенная
оценка экологического состояния
Экологическое состояние природных экосистем
Волжского бассейна в настоящее время характеризуется активным изменением
структурно-функционального облика. На рис. 22 представлена картограмма
обобщенного показателя оценки экологического состояния территории.
|
1 - наилучшая; 4 - наихудшая
В
центре - "наилучшее" состояние по выбранным показателям, внешняя
граница- "наихудшее" состояние по
выбранным показателям. |
|
Рис.
22 Оценка экологического состояния |
Для построения этой обобщенной оценки было
использовано 13 частных показателей, перечень и пространственное распределение
которых представлено ниже:
1.
Лесистость (%) и лесовосстановление (га/км2) поскольку известно, что важное значение для
создания благоприятных экологических условий играют леса, наличие которых и их
восстановление является приоритетной задачей на национальном и мировом уровне.
Санитарно-гигиенические функции леса проявляются в улучшении микроклимата,
оздоровлении воздуха, шумопоглощении.
|
Лесовосстановление
в 2001 г., га/км2 |
Лесистость,
% |
3. Доля заповедных площадей к общей
площади территории. Создана сеть особо охраняемых природных территорий для
предотвращения деградации, восстановления и сохранения уникальных природных
комплексов, флоры, фауны Волжского бассейна.
4. Плотность населения, чел./км2. Демографический
фактор (численность и плотность населения), распределение его по территории
региона прямо воздействует на экосистемы, по нему можно судить и о степени
промышленной и сельскохозяйственной нагрузок и связанных с ними уровнях
загрязнения (атмосферы, воды, почвы).
|
Доля
заповедных площадей, баллы |
Плотность
населения, чел./км2 |
5. Обобщенная сельскохозяйственная
нагрузка (баллы). Этот обобщенный показатель получен с помощью алгоритма
"Комплекс" как сумма баллов "выноса" элементов питания с
урожаем, животноводческой нагрузки, мелиорации, внесения удобрений,
использования сельскохозяйственной техники и пр.
Для получения высоких урожаев в сельском
хозяйстве широко применяется внесение минеральных удобрений. Однако химизация земледелия
высокоэффективно только при условии грамотного и рационального использования
удобрений, обусловленного благоприятными сроками и оптимальными дозами их. Эти
вопросы имеют отношение не только к урожайности растений, но и к охране почв и
природных вод, т.к. внесение повышенных доз минеральных веществ вызывает ряд
отрицательных последствий, вызванных миграцией их неиспользованных остатков в
почвах и природных водах. Ядохимикаты способны накапливаться в почвах,
повреждая фитоценозы и уничтожая сообщества животных, с продуктами поступают в
организм человека, могут откладываться в нем, вызывая различные болезни,
некоторые из которых могут передаваться по наследству. В настоящее время не
создана служба контроля за уровнем токсичных веществ в
почвах.
|
Обобщенная
сельскохозяйственная нагрузка, баллы |
6. Оценка загрязнения воздушного бассейна,
включающая три других показателя: загрязнение атмосферы от стационарных
источников (т/чел.), загрязнение атмосферы автотранспортом (т/чел.)
и оценка метеофакторов накопления загрязнений.
Загрязнение
атмосферы является наиболее опасным по своим последствиям, поскольку
загрязнение некоторыми соединениями приобрело глобальный характер и может
повлечь за собой изменения в биосфере в целом. Значительное ухудшение качества
водной среды, почвы имеет вторичный характер - оно происходит при осаждении,
вымывании поллютантов из атмосферы. Опасность загрязнения атмосферы повышается
и в результате большей чувствительности к ним организмов. Объем необходимого
для дыхания воздуха не сравним с необходимым для жизни количеством воды, пищи.
Различные
производства оказываются не в равной степени опасными для человека. Наиболее
неблагоприятные условия создаются в городах с развитой черной и цветной
металлургией, нефтеперерабатывающей промышленностью, производством удобрений и
зачастую скрывающимися под ними химическими предприятиями военного комплекса.
Существенное ухудшение экологической обстановки вызывает неблагоприятные
сочетания производств, например химические производства с выбросами,
однонаправленного действия на организм, нередко сопровождающимися эффектами
синергизма и потенцирования.
Автомобильный транспорт - наиболее
экологически неблагополучный в силу его многочисленности и рассредоточения.
Основное его воздействие - загрязнение атмосферы и почвы. Загрязнение воздуха
автотранспортом нередко превышает половину загрязнения от всех стационарных
источников. Можно считать автомобильный транспорт наиболее существенным
фактором загрязнения в городах, в значительной степени определяющим загрязнение
всех сред и влияющим на здоровье человека.
Влияние загрязнения атмосферы на здоровье
населения зависит от характера и интенсивности загрязнения и условий циркуляции
воздуха. Практически все известные случаи массового поражения людей возникают
при штилевой погоде, особенно в сочетании и температурной инверсией и
повышенной влажностью воздуха вызванных этим фактором последствий. Оценка
метеофакторов накопления загрязнений включает количество осадков, число дней с
туманами, повторяемость штилей.
|
Оценка
метеофакторов накопления загрязнений |
Загрязнение
атмосферы от стационарных источников, баллы |
|
Загрязнение
атмосферы от автотранспорта, баллы |
Оценка
загрязнения воздушного бассейна, |
7. Оценка
использования водных ресурсов, которая включает в себя 5 параметров: объем
водопотребления из природных источников, использование свежей воды на хоз.питьевые нужды, сброс загрязняющих сточных вод, удельный
вес проб не соответствующие гигиеническим нормативам по санитарно-химическим
показателям и по микробиологическим показателям (по данным Минприроды России,
Госкомстата России). Полученный показатель позволяет районировать территорию
Волжского бассейна по степени воздействия на водные экосистемы.
Главным источником
загрязнения являются сточные воды (в том числе и разной степени очистки)
предприятий нефтехимической, химической промышленности, машиностроения,
целлюлозо-бумажной промышленности, производства удобрений, энергетики и других
отраслей промышленности; хозяйственно-бытовые сточные воды городов и населенных
пунктов, предприятий сельскохозяйственного производства, а в период навигации -
речной транспорт.
Показатель
обеспеченности водными ресурсами включает в себя два исходных показателя:
природная обеспеченность поверхностными водными ресурсами (тыс.м3/чел. в год) и потенциальные ресурсы подземных
вод (тыс.м3/чел. в год). Пространственное распределение
обеспеченности водными ресурсами и забора воды из природных источников
прологарифмировано, переведено в баллы и представлено на рис.
|
Обеспеченность
водными ресурсами, баллы |
Забрано
воды из природных источников, баллы |
|
Оценка
по использованию водных ресурсов, баллы |
8. Образование токсичных отходов (т/чел.).
9. Оценка затрат
на охрану природы, включает следующие показатели: затраты предприятий на охрану
водных ресурсов (без кап.вложений); кап.вложения на охрану
земель, затраты предприятий на охрану и рекультивацию земель (без
кап.вложений); кап.вложения на охрану воздуха; использование капитальных
вложений на охрану окружающей среды.
Загрязнение
окружающей среды и снижение качества конечной продукции (с точки зрения ее экологической чистоты и безопасности) ведет и к росту
затрат на преодоление негативных последствий этих процессов. В результате все
большая доля совокупного общественного труда тратится на обезвреживание
отходов, очистку сточных вод, восстановление нарушенных природных ресурсов.
Расширяются границы сферы общественного производства за счет появления новых
видов природоохранной деятельности, очистных производств и т.д. При этом
относительная величина природоохранных затрат может сильно меняться в
зависимости от реализуемого этапа эколого-экономической стратегии развития
национальной экономики и от преимущественно применяемых методов регулирования
охраны среды. Оптимальный на сегодняшний день объем экологических затрат для
стабилизации и улучшения экологической обстановки в странах с развитой рыночной
экономикой оценивается примерно в 3-4% валового национального продукта.
|
Образование
токсичных отходов, т/чел. |
Оценка
затрат на охрану природы |
10. Оценка
заболеваемости населения включает 5 показателей: общая заболеваемость на 1000
чел.; болезни органов пищеварения на 1000 чел.;
болезни органов дыхания на 1000 чел.; инфекционные и паразитарные заболевания
на 1000 чел.; новообразования на 1000 чел.
Заболеваемость
населения выступает как один из многих биоиндикаторов, характеризующих
экологическое состояние территории и является интегральным показателем качества
среды [4-6] отражает суммарный эффект влияния нескольких факторов в их
взаимодействии, включающим синергизм (взаимное усиление), антагонизм
(ослабление, нейтрализация), кумуляцию (накопление во времени).
|
Оценка
заболеваемости населения |
Для построения
комплексного показателя антропогенной нагрузки на территорию Волжского бассейна
(алгоритм "Комплекс") были использованы следующие показатели: обобщенный
показатель загрязнение атмосферы, обобщенный показатель воздействия на водные
ресурсы, обобщенная с/х нагрузка. Обобщенный показатель загрязнения атмосферы
учитывает загрязнение от стационарных источников по различным составляющим и
загрязнение от автомобильного транспорта. Обобщенная характеристика
использования водных ресурсов включает в себя 23 параметра (объемы
водопотребления и водоотведения, объемы выбрасываемых загрязняющих веществ по
отдельным ингредиентам, строительство очистных сооружений, вложение средств в
охрану водных ресурсов). Обобщенная с/х нагрузка - см. выше.
|
Антропогенная
нагрузка, баллы |
Распределение видов
наземных позвоночных по территории Волжского региона неравномерно, что связано
с большой площадью региона и его значительной протяженностью с севера на юг и,
в меньшей степени, с запада на восток и связанных с этим изменений температуры
и влажности. В целом, разнообразие видов млекопитающих
увеличиваясь с севера на юг, доходит до своего максимума в центральных районах
Волжского бассейна и далее на юг вновь уменьшается. Такая же закономерность
характерна и для земноводных. Пресмыкающиеся демонстрируют четкое увеличение
разнообразия с севера на юг. На севере лимитирующим фактором распространения
наземных позвоночных являются низкие температуры. Особенно это проявляется на
земноводных и пресмыкающихся.
|
Разнообразие
пресмыкающихся |
Разнообразие
земноводных |
Табл.
Показатели
по площади и численности населения
|
|
Площадь,
тыс.км2 |
Численность
населения, тыс.чел., 1989 г. |
Плотность
населения, чел./км2
1989
г. |
Численность
населения, тыс.чел., 2002 г. |
Плотность
населения, чел./км2
2002 г. |
|
Тверская обл. |
84,1 |
1670 |
19,9 |
1676 |
19,9 |
|
Ярославская обл. |
36,4 |
1471 |
40,4 |
1367 |
37,6 |
|
Костромская обл. |
60,1 |
809 |
13,5 |
737 |
12,3 |
|
Ивановская обл. |
23,9 |
1317 |
55,1 |
1148 |
48,0 |
|
Владимирская обл. |
29,0 |
1654 |
57,0 |
1524 |
52,6 |
|
Московская обл. |
47,0 |
15653 |
333,0 |
17002 |
361,7 |
|
Нижегородская обл. |
74,8 |
3713 |
49,6 |
3524 |
47,1 |
|
Рязанская обл. |
39,6 |
1346 |
34,0 |
1228 |
31,0 |
|
Тульская обл. |
25,7 |
1868 |
72,7 |
1676 |
65,2 |
|
Калужская обл. |
29,9 |
1067 |
35,7 |
1042 |
34,8 |
|
Мордовия |
26,2 |
964 |
36,8 |
889 |
33,9 |
|
Пензенская обл. |
43,2 |
1502 |
34,8 |
1453 |
33,6 |
|
Чаваш Республика |
19,3 |
1336 |
73,0 |
1314 |
68,1 |
|
Марий Эл |
23,2 |
750 |
32,3 |
728 |
31,4 |
|
Кировская обл. |
120,8 |
1694 |
14,0 |
1503 |
12,4 |
|
Татарстан |
68,0 |
3640 |
53,3 |
3780 |
55,6 |
|
Урдмудская |
42,1 |
1609 |
38,2 |
1570 |
37,3 |
|
Ульяновская обл. |
37,3 |
1400 |
37,5 |
1382 |
37,1 |
|
Самарская обл. |
53,6 |
3266 |
60,9 |
3239 |
60,4 |
|
Башкортостан |
143,6 |
3952 |
27,5 |
4104 |
28,6 |
|
Саратовская обл. |
100,2 |
2690 |
26,8 |
2668 |
26,6 |
|
Пермская обл. |
160,6 |
3100 |
19,3 |
2819 |
17,6 |
|
Волгоградская обл. |
113,9 |
2593 |
22,8 |
2699 |
23,7 |
|
Астраханская обл. |
44,1 |
998 |
22,6 |
1005 |
22,8 |
Литература
1.
Розенберг
Г.С., Краснощеков Г.П.
Волжский бассейн: экологическая ситуация и пути рационального
природопользования. – Тольятти: ИЭВБ РАН, 1996. - 249 с.
2.
Краснощеков Г.П., Розенберг Г.С. Естественно-исторические
аспекты формирования территории Волжского бассейна // Изв. СамНЦ РАН. 1999. Т.
1. № 1. С. 108-117.
3.
Найденко В.В. Великая
Волга на рубеже тысячелетий. От экологического кризиса к устойчивому развитию.
В 2-х т. – Н.Новгород: Промгафика, 2003. – Т. I. – 432 с.; Т. II. – 368 с.
4.
Экологическое состояние
окружающей среды бассейна реки Волги (1995-2001 гг.). - Н. Новгород, 2002. -
129 с.
5.
Краснощеков Г.П., Розенберг Г.С. Здоровье населения как критерий оценки качества
среды. - Тольятти: ИЭВБ РАН, 1994. - 53 с.
6.
Пуртов
И.И., Гелашвили Д.Б., Моничев А.Я., Басуров В.А. Подходы к оценке антропогенной нагрузки на территорию
с учетом основных показателей здоровья населения. Гигиена и сан. 2001, № 4, с.
70-72.
8.
Примеры картограмм по Самарской области
Территория
Самарской области составляет 53,6 тыс.км2 (0,13%
площади Российской Федерации), протяженность области с севера на юг - 335 км, с
запада на восток - 315 км, она включает 27 административных района, имеет
уникальное и очень выгодное ландшафтно-географическое положение. Самарская
область характеризуется развитой промышленностью, интенсивным сельским
хозяйством, высокой плотностью населения (60,4 чел./км2). По показателям уровня жизни Самарская
область относится к группе наиболее благополучных территорий Волжского
бассейна.
Территория
Самарской области была разбита на 287 участков, по которым в базе данных было
оцифровано около 300 показателей. Построен целый ряд обобщенных (комплексных)
показателей, характеризующих экологическую ситуацию [1-6].
Для построения
обобщенного показателя оценки экологического состояния территории Самарской
области (рис. 23) было включено 8 показателей, картограммы
распределения которых представлены ниже.
|
|
|
Рис.
23. Оценка экологического состояния Самарской области |
Список использованных частных показателей:
1. Уровень лесистости, %.
2. Видовое разнообразие животных
(информационный индекс Шеннона-Уивера).
|
Рис.
Уровень лесистости, % |
Рис.
Видовое разнообразие животных |
3. Обобщенная
характеристика использования воды, включающая 23 параметра (объемы
водопотребления и водоотведения, объемы выбрасываемых загрязняющих веществ по
отдельным ингредиентам).
4. Обобщенная
оценка загрязнения атмосферного воздуха, основанная на синтезе нескольких
параметров (пространственная организация промышленности, обобщенная оценка
энергетической нагрузки, загрязнение воздуха отдельными предприятиями).
|
Обобщенная
характеристика использования воды, баллы |
Обобщенная
оценка загрязнения атмосферы, баллы |
5. Обобщенная транспортная нагрузка.
6. Обобщенная
сельскохозяйственная нагрузка, включающая ряд показателей: воздействие
эрозионных процессов, "вынос" элементов питания с урожаем, заготовка
сена, общая животноводческая нагрузка, общая пестицидная нагрузка, площади
сельскохозяйственных угодий и пашни, внесение минеральных удобрений в переводе
на действующее вещество, наличие солонцов, солонцовых и засоленных почв.
|
Обобщенная
сельскохозяйственная нагрузка, баллы |
Комплексный
показатель транспортной нагрузки, баллы |
7. Комплексный показатель детской заболеваемости,
включающий различные классы болезней.
8. Комплексный показатель заболеваемости
взрослого населения.
|
Комплексный
показатель детской заболеваемости, баллы |
Комплексный
показатель заболеваемости взрослого населения, баллы |
Интересно также рассмотреть отдельно
картограммы комплексных показателей рекреационной и общей антропогенной
нагрузки, представленные ниже.
|
Комплексный
показатель рекреационной нагрузки, баллы |
Комплексный
показатель антропогенной нагрузки, баллы |
Литература
1. Экологическая ситуация в Самарской области / Под
ред. Г.С.Розенберга и В.Г. Беспалого. Тольятти, 1994. - 326 с.
2. Шапеева Е.В., Юрицына Н.А., Лифиренко
Н.Г., Юнина В.П., Афанасьева Н.В.
Эколого-информационные системы разных масштабов для комплексной оценки состояния
природной среды в регионах с интенсивной антропогенной нагрузкой (город,
область, Волжский бассейн). - Тольятти, ИЭВБ РАН, 1994. - 53 с.
3. Экологическая обстановка Самарской области в 1990-1997 гг. и инвестиции на
охрану окружающей среды. - Самара, 1998. - 150 с.
4. Костина Н.В. Эколого-информационная система большого региона как
основа экологического мониторинга. // Региональный экологический мониторинг в
целях управления биологическими ресурсами. Тольятти: ИЭВБ РАН, 2003. С.
152-158.
5. Костина Н.В., Пыршева М.В. Система "Здоровье населения - окружающая
среда" в региональном аспекте // Окружающая среда и здоровье: Сб.
материалов всерос. науч.-практ. конф. – Пенза, 2004. –
С. 94-96.
6. Государственные доклады о состоянии окружающей природной среды Самарской
области в 1998-2003 гододах. Экологическая безопасность и устойчивое развитие
Самарской области. Вып. 8-14. - Самара, 1999-2004. - от 101 до 216 с.
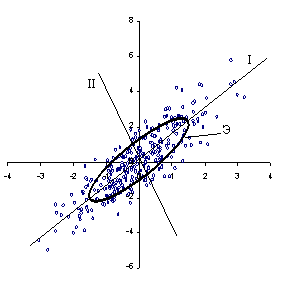

 б)
б)