Актуальность работы. Бурное развитие информационных технологий и компьютерной техники послужило толчком к развитию общества, построенного на использовании различной информации и к возникновению идеи применения искусственного интеллекта в современной вычислительной технике. Исследования искусственных нейронных сетей составляют значительные разделы в таких науках, как биофизика, вычислительная математика, электроника. Нейросети применяются для решения задач искусственного интеллекта, в системах технических органов чувств, ядерной физике, геологии, управлении производственными процессами и социально-экономическими системами.

Подход к обработке информации, основанный на применении нейронных сетей, не требует готовых алгоритмов и правил – система должна “уметь” самостоятельно вырабатывать правила и модифицировать их в процессе решения конкретных задач. Для многих задач, где такие алгоритмы неизвестны, или же известны, но требуют значительных затрат на разработку программного обеспечения, нейросети предлагают исследователю эффективные, легко и быстро реализуемые методы решения. И это делает нейронные сети универсальным инструментом обработки информации, а разработка методов нейросетевого моделирования и анализа информации представляют большой интерес.

Стремительный рост объемов используемой информации ведет к усложнению алгоритмов прямой обработки с помощью различных способов и методов, увеличению временных затрат, усложнению процедур оптимизации и, как следствие, к снижению точности решения задач. С увеличением числа изучаемых объектов все большее распространение получают эмпирические зависимости (формулы, алгоритмы). В отличие от теоретических зависимостей, эмпирические зависимости не единственны. Поэтому возникает необходимость выбора “наилучшего” варианта зависимости из полученных альтернатив.

Наиболее распространенным подходом получения “наилучших зависимостей” является уменьшение числа исходных данных (минимизация описания). Этот подход позволяет решать задачи отбора наиболее информативных данных, сжатия массивов обрабатываемой и хранимой информации, задачи наглядного представления данных (визуализация данных). Однако такого рода операция с данными, безусловно, ведет к потере части полезной информации и ограничениям в использовании дополнительных априорных сведений о решаемой задаче. Поэтому все чаще возникает вопрос: насколько хорош созданный минимальный набор параметров?

В зависимости от решаемой задачи ответ на этот вопрос может быть разным. Если все входные параметры являются объективными (например, результатами физических измерений), то минимального набора параметров достаточно для качественного решения задачи. Однако если входные параметры являются субъективными (например, экспертная оценка) или решение чувствительно к изменению значения измеряемой величины, меньшему чем точность измерения, то минимальный набор ненадежен.

В условиях сокращения (минимизации) описания все чаще возникают проблемы повышения качества нейросетевых решений и их надежности в случаях искажения информации во входных данных, а также выявление взаимосвязей между признаками в процессе решения поставленных задач. Как правило искажение информации во входных данных возникает в двух случаях: либо это случайные (неумышленные) ошибки исследователя в процессе формирования выборки, либо преднамеренное искажение данных. И хотя на сегодняшний день существуют инструменты позволяющие контролировать качество входной информации, однако все они основаны на проверке качества работы исследователя, а это не значит, что ошибка, допущенная одним человеком, не может быть пропущена другим.

Поэтому на сегодняшний день решение задачи повышения устойчивости нейросетевой системы (в условиях сокращения количества входных данных и возможного искажения информации) является актуальной.

В диссертационной работе решение поставленной задачи производится посредством поиска компромисса, то есть добавления к минимальному набору такого набора признаков, который содержит в себе данные, полностью или частично дублирующие информацию из минимального набора.

Цель работы. Разработка метода повышения качества решения задач в условиях искажения информации во входных данных и минимизации пространства признаков.

Для достижения указанной цели были поставлены следующие задачи.

· Разработка теоретических основ метода.

· Построение алгоритмов реализации метода.

· Формирование структурных схем зависимости признаков.

· Применение метода при решении задачи классификации осложнений инфаркта миокарда.

· Апробация метода в процессе решения задачи прогнозирования результативности труда преподавателя.

В рамках реализации цели и задач диссертационной работы сделано следующее.

В первой главе дана характеристика основных понятий категории “информация” и ее особенностей. Описан круг задач, связанных с обработкой данных. Дан обзор и анализ традиционных методов и алгоритмов обработки информации. Проведено обзорное исследование алгоритмов восстановления зависимостей и методов снижения размерности выборки. Обоснован выбор нейросетевых подходов к обработке информации как наиболее универсального инструмента и описаны основные элементы нейросетей. Рассмотрены проблемы возникновения искажений информации и существующие способы их устранения. Поставлена задача создания компромиссной модели формирования выборки, которая удовлетворяла бы и решению задачи снижения размерности и задачи повышения устойчивости решений к искажениям во входных данных. В качестве базы для решения поставленной задачи предложена идея поиска дублирующих признаков. Введено понятие дублирования информации – как способа повышения качества обработки данных и предсказания поведения объекта.

Во второй главе подробно охарактеризован круг задач, успешного решения которых можно достигнуть с помощью дублирования информации. Дано формальное описание основных понятий, применяемых в процессе создания методологии дублирования. На базе предложенных понятий сформирована классификация дублей. Исходя из предложенной классификации определены четыре возможных варианта дублей: прямой дубль первого рода (ПДПР), косвенный дубль первого рода (КДПР), прямой дубль второго рода (ПДВР), косвенный дубль второго рода (КДВР). Далее последовательно рассмотрены подходы и алгоритмы получения каждого дубля в отдельности и, на их основе, наборов повышенной надежности для решения задачи в условиях возникновения искажений информации. На базе каждого из дублей сформирована структурная схема зависимости признаков в рамках решения поставленной задачи. С помощью теорем доказано соотношение между различными видами дублей.

В главе три показано практическое применение методологии дублирования информации на примере решения задачи классификации предсказаний летального исхода в случае наступления инфаркта миокарда. В процессе решения задачи найдено три вида дублей: прямой дубль первого рода, прямой дубль второго рода и косвенный дубль второго рода. На базе полученных дублей построены структурные схемы зависимостей признаков. В ходе проведения экспериментов доказано, что для выборки по осложнениям инфаркта миокарда наборы повышенной надежности на базе каждого из дублей по праву носят свое название, так как результаты работы нейронной сети в условиях искажения входной информации лучше, чем в случае с набором прототипов.

В четвертой главе получены результаты при решении задачи прогнозирования результата деятельности преподавателя со студентами. Найдены все виды дублей, на их основе построены наборы повышенной надежности. В качестве системы, способной решать поставленную задачу со всеми ограничениями в условиях возможных искажений информации во входных данных, выбрана нейронная сеть с набором признаков, обладающим повышенной надежностью и построенном на базе прямого дубля первого рода. Построены схемы иерархической структуры пространства признаков.

Научная новизна диссертации заключается в следующем:

· впервые предложен метод дублирования информации, позволяющий повысить качество решения задач в условиях возникновения искажений информации во входных данных;

· построены алгоритмы поиска дублирующих наборов и формирования иерархических схем зависимости признаков;

· предложенный метод дублирования реализован с помощью нейросетевых технологий обработки данных;

· на конкретных примерах исследовано влияние дублирования информации на качество решения задач прогнозирования и классификации.

Практическая значимость. Предложенные в работе методы построения наборов признаков повышенной устойчивости к искажениям входной информации с помощью различных видов дублирования могут применяться при решении задач в различных областях. На примере решения задачи классификации предсказаний летального исхода в случае наступления инфаркта миокарда и задачи прогнозирования результативности деятельности преподавателя показана эффективность использования предложенных методов. Полученные результаты представляют интерес для создания методов анализа и обработки данных не только в медицине и в процессе управления персоналом в социально-экономических системах, но и в других областях.

Представленный в работе подход к выявлению зависимостей в пространстве признаков позволяет сократить и упростить работу над созданием иерархической структуры данных. Метод, реализованный на имитаторе нейронной сети, открывает путь к оптимизации моделей, созданных на базе искусственных нейронных сетей по принципу достаточного для данной задачи объема информации.

Предложенный метод построения дублирующих множеств может реализовываться и с помощью других инструментов построения эмпирических зависимостей.

Результаты, выносимые на защиту:

1. Метод дублирования информации, как средство повышения устойчивости решений в условиях искажения входных сигналов.

2. Классификация дублирующих наборов, сформированная на базе сочетания двух принципов: по объекту дублирования и по способу определения.

3. Алгоритмы построения дублирующих наборов на основе предложенной классификации.

4. Апробация метода на задачах классификации и прогнозирования. Подтверждение повышения устойчивости решений нейросетевой системой на базе наборов, сформированных на основе различных видов дублирования, в условиях искажения входной информации.

Публикации. Основные результаты работы, полученные при выполнении диссертационных исследований, опубликованы в 11 печатных работах, из них 6 статей и 5 тезисов докладов.

Апробация работы. Материалы диссертации докладывались на Межрегиональной конференции студентов и аспирантов “Теория и практика коммерческой деятельности” 29 февраля 2000 года, на Региональной межвузовской научно-практической конференции “Социально-экономические проблемы развития рынка потребительских товаров” 24.03.2000г., на Всероссийской научно-практической конференции с международным участием “Достижение науки и техники – развитию сибирских регионов (инновационный и инвестиционный потенциалы)” в марте 2000 года, на III Международной научно-практической конференции “Экономические реформы в России” в Санкт-Петербурге в апреле 2000г., на открытом методическом семинаре кафедры “Менеджмента” Красноярского государственного торгово-экономического института 26.11.99г., на семинаре кафедры системотехники Сибирского государственного технологического университета весной 2000 года, на городском семинаре по Нейроинформатике в Институте вычислительного моделирования СО РАН г. Красноярска в 2001 году.

ГЛАВА 1. ИНФОРМАЦИЯ КАК ОБЪЕКТ ИССЛЕДОВАНИЙ

1.1. Информация и информационная технология

Современное общество живет в период, одну из характерных черт которого составляет информатизация. Под информатизацией общества понимается повсеместная реализация мер, обеспечивающих возможность своевременного получения и использования полной и достоверной информации во всех областях знаний и видах человеческой деятельности [55].

Информация – это одна из сложнейших, еще полностью не раскрытых, даже таинственных проблем современной науки. Это следует хотя бы из нечеткости самих определений понятия информации – совокупность сведений, данных, знаний или информация есть знание об особом факте, событии, или ситуации [19, 55, 69].

Как и любой объект изучения, информация имеет свои четко определенные показатели качества, систему классификации, инструменты и методы обработки, средства и способы защиты [95] и т.п. Каждый из видов информации содержит смысловую ценность, требования к точности, достоверности и оперативности отражения факторов, определенные формы представления и фиксации на физическом носителе, а процесс её переработки по аналогии с процессами переработки материальных ресурсов можно воспринимать как технологию.

Информационная технология – процесс, использующий совокупность средств и методов сбора, обработки и передачи данных (первичной информации) для получения информации нового качества о состоянии объекта, процесса или явления [55]. По сути, под информационной технологией на практике понимается технологическое применение компьютеров и других технических средств обработки и передачи информации.

Как и всякая технология, информационная технология включает в свой состав определенные комплексы материальных средств (носители информации, технические средства ее измерения, передачи, обработки и т.п.), способы их взаимодействия, а также определенные методы организации работы с информацией. К настоящему моменту времени информационная технология прошла несколько эволюционных этапов, смена которых определялась главным образом развитием научно-технического прогресса и появлением новых технических средств переработки информации.

Информационная технология имеет достаточно большое количество разновидностей, но, несмотря на это, она представляет собой процесс, состоящий из чётко регламентированных правил выполнения операций, действий, этапов (разной степени сложности) над данными, хранящимися в компьютерах. Основная цель этого процесса состоит в получении необходимой для пользователя (исследователя) информации в результате целенаправленных действий по переработке первичных данных.

Понятие информационной технологии тесно связано с информационными системами, которые являются для неё основной средой существования.

Информационная система – человеко-компьютерная система для поддержки принятия решений и производства информационных продуктов, использующая компьютерную информационную технологию [55, 69]. Из всего многообразия компьютерных информационных систем наиболее распространенными являются системы обеспечения принятия решения. Составляющими элементами такой системы являются компьютеры, компьютерные сети, программные продукты, базы данных, люди, различного рода технические и программные средства связи и т. д.

Идеальная система обеспечения принятия решения – это динамическая система с непрерывным обновлением данных, развитием которой являются экспертные системы. Эти системы представляют собой компьютерные программы, включающие базы знаний по частным проблемам и механизмы взаимодействия элементов этих баз и являются по сути интеллектуальными.

База знаний таких систем включает в себя большую сумму знаний относительно проблем, запомненных в системе. Исследователи находят, что использование этой массы знаний более эффективно, чем использование специальных решающих процедур. Поэтому экспертные системы являются консультантами в принятии решений, так как содержат факты, знания и правила, которые взаимодействуют в проблемной области.

Выгоды оперирования реальным знанием и способности экспертных систем ведут к созданию и использованию систем с искусственным интеллектом, центральным правилом которых является скорее использование правил эвристики (или перебора), чем алгоритмов обработки информации.

Независимо от вида информационной системы основная цель ее существования – это организация хранения и передачи информации. Так как информационная система представляет собой человеко-компьютерную систему обработки информации [69, 84], то процессы, обеспечивающие работу информационной системы, включают в себя несколько блоков [56]:

· ввод информации из внешних или внутренних источников;

· обработка входной информации и представление её в удобном виде;

· вывод информации для представления потребителям или передачи в другую систему;

· обратная связь – это информация, переработанная людьми для коррекции входной информации.

Основной компонент информационной системы – технические средства. Техническими средствами производства информации является аппаратное, программное и математическое обеспечение этого процесса. С их помощью производится переработка первичной информации в информацию нового качества.

Математическое и программное обеспечение – это совокупность математических методов, моделей, алгоритмов и программ для реализации целей и задач информационной системы, а также нормального функционирования комплекса технических средств [5]. К ним относятся: средства моделирования процессов; типовые задачи; методы математического программирования, математической статистики, теории массового обслуживания и др.

В состав программного обеспечения входят общесистемные и специальные программные продукты, а также техническая документация. Они предоставляют исследователю ряд качественно новых технических возможностей в формировании статистического материала, в регистрации, обработке и отображении полезной информации [59].

Наиболее активно развивающимся направлением компьютерной информационной технологии на сегодняшний день является анализ данных. Эта обширная область, которая включает в себя совокупность методов и средств извлечения из определенным образом организованных данных информации нового характера для принятия решений [68, 78]. При этом методы анализа данных реализуются в виде различных пакетов прикладных программ, в состав которых входят известные процедуры математики, математической статистики и др. Применение таких программ основано на реализации восьми этапов:

1) установочный (предметно-содержательное определение целей);

2) постановочный (определение типа прикладной задачи);

3) информационный (составление плана сбора исходной информации и его реализация, затем предварительный анализ исходной информации, ее ввод в ЭВМ, сверка, редактирование);

4) априорный математико-постановочный (осуществляемый до каких бы то ни было расчетов выбор базовой математической модели механизма генерации исходных данных);

5) разведочный (специальные методы статистической обработки исходных данных);

6) апостериорный математико-постановочный (уточнение базовой математической модели с учетом результатов предыдущего этапа);

7) вычислительный (реализация на ЭВМ уточненного на предыдущем этапе плана математико-статистического анализа данных);

8) итоговый (подведение итогов исследования, формулировка научных или практических выводов).

Широкое применение различных методов анализа и обработки информации, а так же компьютерной техники предъявляет повышенные требования к качеству обрабатываемой информации на всех этапах ее прохождения. Однако практика показывает, что в процессе формирования исходной информации исследователь не застрахован от ошибок. В зависимости от характера, стадии и причин различают несколько типов ошибок (табл. 1.1).

Таблица 1.1

Классификация ошибок наблюдения [80]

Признаки классификации	Виды ошибок
Характер ошибок	Случайные Систематические
Стадия возникновения	Ошибки регистрации Ошибки при подготовке данных к обработке Ошибки в процессе обработки
Причины возникновения	Ошибки измерения Ошибки репрезентативности Преднамеренные ошибки Непреднамеренные ошибки

В настоящее время можно выделить большое количество причин возникновения такого рода ошибок в процессе формирования первичных данных – это приписки, безответственность, некомпетентность и другие как умышленные, так и неумышленные искажения исходной информации. И естественно, что в рамках развития современной науки разрабатываются методы выявления и предупреждения ошибок. Однако до сих пор нередкими являются случаи искажения значений информации, ведущие к принятию ошибочных решений, недостоверных исследований, дополнительным затратам времени и т.п.

Таким образом, к основным компонентам информационной технологии можно отнести: сбор данных, обработку данных и их хранение. При этом наиболее ответственным этапом для исследователя является именно сбор данных, а наиболее сложным – обработка и анализ данных [13, 37]. Это связано с необходимостью выполнения таких операции, как: классификация или группировка; сортировка, с помощью которой упорядочивается последовательность записей; вычисления, включающие арифметические и логические операции; укрупнение или агрегирование, служащее для уменьшения количества данных.

1.2. Алгоритм и традиционные методы обработки информации

Развитие электронно-вычислительной техники, как средства обработки больших массивов данных, стимулировало проведение комплексных исследований сложных социально-экономических, технических, медицинских и других процессов и систем. В связи с многоплановостью и сложностью этих объектов и процессов данные о них носят, как правило, многомерный и разнотипный характер, в связи с этим исследователю приходиться прибегать к специальному математическому инструментарию многомерного статистического анализа.

К числу основных методологических принципов, которые лежат в основе большинства конструкций многомерного статистического анализа, следует отнести следующие принципы [2, 3].

1. Необходимость учета эффекта существенной многомерности анализируемых данных (используемые в конструкциях характеристики должны учитывать структуру и характер статистических взаимосвязей исследуемых признаков).

2. Возможность лаконичного объяснения природы анализируемых многомерных структур (допущение, в соответствии с которым существует сравнительно небольшое число определяющих, подчас латентных, то есть непосредственно не наблюдаемых, факторов, с помощью которых могут быть достаточно точно описаны все наблюдаемые исходные данные, структура и характер связей между ними).

3. Максимальное использование “обучения” в настройке математических моделей (под “обучением” понимается та часть исходных данных, в которой представлены “статистические фотографии” соотношений “входов” и “выходов” анализируемой системы). Если исследователь располагает и “входами” и “выходами” задачи, то исходную информацию называют обучающей и целью исследования является описание процедур, с помощью которых при поступлении только входных данных нового объекта его можно было бы с наибольшей точностью вычислить результат, отнести к одному из классов или снабдить значениями определяющих факторов. Именно к таким ситуациям относятся типичные задачи медицинской диагностики, когда в клинических условиях в качестве исходных данных исследователь располагает как “входами” — результатами инструментальных обследований пациентов, так и “выходами” — уже установленным диагнозом по каждому из них. Цель исследований такого типа — использование имеющегося “обучения” для отбора из множества результатов обследований небольшого числа наиболее информативных показателей и для построения на их основе формального диагностирующего правила.

4. Возможность оптимизационной формулировки задач многомерного статистического анализа (то есть нахождение наилучшей процедуры статистической обработки данных с помощью оптимизации некоторого заданного критерия качества метода).

На этапе сбора информации исследователь создает базу данных с помощью различных статистических методов, которые позволяют создавать обучающую выборку, оформленную (как правило) в виде таблиц данных. (Под “базой данных” понимается вся необходимая для решения определенного класса задач информация, записанная на машинных носителях и организованная по определенным правилам, обеспечивающим удобство хранения, поиска и преобразования.) Эти таблицы содержат в себе пространство признаков, характеризующих объекты изучения (примеры).

При формировании исходного множества признаков исследователь располагает большой свободой и, как следствие, сложностью в определении полноты выбранного множества. Поэтому формирование исходного множества признаков является трудно формализуемой задачей и для ее решения предлагается лишь ряд общих рекомендаций [49, 70]. В целом этот процесс формирования исходного множества (особенно при конструировании базы данных) является трудоемким и тонким занятием, а качество его выполнения полностью зависит от знаний, опыта и интуиции специалиста, выполняющего работу.

Кроме того, в процессе дальнейшей работы с данными, перед исследователем чаще всего возникают проблемы восстановления значения результата по значениям “сопутствующих” переменных; классификации объектов или признаков; исследования зависимостей между анализируемыми показателями и снижение размерности исследуемого факторного пространства [64, 80]. Поэтому стоит обратить внимание именно на методы обработки данных и решение некоторых поставленных задач.

В статистике выделяют две основные группы методов (табл. 1.2), способных установить зависимости между признаками или объектами выборки: первая основана на критерии автоинформативности экспериментальных данных, а вторая – на использовании внешних критериев [2, 3].

Таблица 1.2

Методы определения структуры данных

Название	Смысловая ценность критерия информативности	Используемые предположения о структуре данных
Метод главных компонент	Выявление в пространстве исходных признаков новой координатной оси с максимальной дисперсией	Основная часть исходных признаков согласованно отражает требуемых конструкт
Факторный анализ	Максимальная точность воспроизведения корреляционных связей между исходными признаками с помощью новых вспомогательных переменных	Одна или несколько групп взаимосвязанных признаков отражают один или несколько диагностических конструктов
Метод контрастных групп	Исключение признаков из “чернового” варианта выборки, уменьшающих вытянутость гиперэллипсоида рассеивания	Большая часть признаков подобрана правильно
Регрессионный анализ	Минимизация ошибки восстановления значений критериального показателя по значениям исходных признаков	Значения критериального показателя линейно связаны с признаками
Дискриминантный анализ	Минимизация вероятности ошибочного отнесения объектов к заданным классам	Критериальный показатель является номинальной величиной
Типологический подход	Минимизация ошибки восстановления критериального показателя для отдельных групп объектов	Нелинейная сложная связь значений критериального показателя с исходными признаками для выборки в целом

Критерии автоинформативности – это такие критерии, оптимизация которых приводит к набору вспомогательных переменных, позволяющих максимально точно воспроизводить информацию, содержащуюся в описательном массиве данных.

Критериями внешней информативности (имеется в виду информативность, внешняя по отношению к информации, содержащейся в описательном массиве) называют такие критерии, которые нацелены на поиск экономных наборов вспомогательных переменных, обеспечивающих максимально точное воспроизведение информации, относящейся к результирующему показателя (результату вычисления).

Методы, основанные на критерии автоинформативности

Формальные алгоритмы данной группы методов не оперируют непосредственно обучающей информацией о значении вычисляемой переменной. Но такая информация в неявном виде всегда присутствует в экспериментальных данных, так как закладывается на этапе формирования исходного множества признаков.

Наиболее распространенным методом из этой группы является метод главных компонент [55, 56, 67]. Алгоритмы, обеспечивающие выполнение данного метода, входят практически во все пакеты статистических программ.

Его суть заключается в переходе к новой системе координат y₁, …, y_p в исходном пространстве признаков x₁, …, x_p, которая является системой ортонормированных линейных комбинаций. Комбинации выбираются таким образом, что среди всех возможных линейных нормированных комбинаций исходных признаков первая главная компонента обладает наибольшей дисперсией, обусловленной взаимосвязанностью признаков, а вторая главная компонента имеет наибольшую дисперсию среди всех оставшихся линейных преобразования, некоррелированных с первой и т.д. Под критерием автоинформативности пространства признаков в методе понимается то, что ценную информацию можно отразить в линейной модели, которая соответствует новой координатной оси в данном пространстве с максимальной дисперсией распределения проекции исследуемых объектов.

В отличие от метода главных компонент факторный анализ основан не на дисперсионном критерии автоинформативности системы признаков, а ориентирован на объяснение имеющихся между признаками корреляций [74]. Поэтому он применяется в более сложных случаях совместного проявления на структуре данных тестируемого и исследуемого свойств объектов. Подробное описание факторного анализа можно найти в [1], [50], [65] и [99].

В основе метода контрастных групп лежит гипотеза о том, что значительная часть исследуемой модели подобрана или угадана правильно, то есть выборка содержит достаточно много признаков, согласовано отражающих исследуемое свойство. В тоже время предполагается наличие определенной доли признаков, создающей ненужный или даже вредный балласт, от которого нужно избавиться [7].

Каждый из рассмотренных методов имеет свое самостоятельное значение для решения конкретных задач обработки информации. Они имеют определенные достоинства и недостатки и могут применяться в совокупности с другими методами.

Методы, использующие внешний критерий

Выделяют три основных группы внешних критериев:

1. Экспертные. К их числу относят оценки, суждения, заключения и т.д., вынесенные экспертом или группой экспертов.

2. Экспериментальные. Экспериментальными критериями внешней информативности служат результаты одновременного и независимого эксперимента. Наиболее целесообразен такой подход, когда ставится задача улучшить характеристики известного инструментария.

3. “Жизненные”. В качестве таких критериев используют объективные данные в области психологии, социологии, медицине, экономике и т.д.

Внешний критерий может быть представлен номинальным, ранговым или количественным показателем, “привязанным” к объектам анализируемой базы данных [3]. Его специфика влияет на выбор метода обработки информации.

С позиции регрессионного анализа критериальный показатель рассматривается как “зависимая” переменная, выраженная функцией от “независимых” признаков [8, 11, 38, 40, 44, 62]. Известно большое количество вариантов такого анализа, опирающихся на различные допущения в структуре данных и свойствах линейной модели. Каждый из них применяется в определенных условиях и имеет конкретное значение.

Если критериальный показатель измерен в номинальной шкале или связь этого показателя с исходными признаками является нелинейной и носит неизвестный характер, то для определения структуры данных используют методы дискриминантного анализа. Для этого объекты выборки в соответствии с внешним критерием разбиваются на классы, а эффективность структуры данных рассматривается как способность дискриминировать даигностируемые классы [8, 44]. Большая часть этих методов основана на байесовской схеме принятия решений о принадлежности объектов к тому или иному классу.

Описание работы типологического подхода можно найти в [61]. Он основан на том, что каждый объект описывается набором характеристик и ему ставится в соответствие значение некоторого критериального показателя. Тогда задача состоит в том, чтобы построить математическую модель, имеющую максимальную корреляцию с критерием или дискриминирующую объекты относительно критериального показателя. Однако этот подход связан с трудно формализуемым и нечетким определением понятия однородности группы объектов.

Процесс статистической обработки данных с помощью рассмотренного инструментария весьма трудоемкий, имеет свои специфические особенности, а создание методики его реализации в определенных условиях требует привлечения специалистов в области статистического анализа.

Более того, по мере роста объемов перерабатываемой информации возможность эффективной реализации подобной логики исследования становится все менее реальной. В настоящее время в исследовательской и практической деятельности все чаще и чаще приходится сталкиваться с ситуациями, когда общее количество признаков по каждому примеру в выборке очень велико – порядка ста и более, а работать с такой информацией просто необходимо. Поэтому понятно желание исследователя существенно сократить объем выборки, чтобы:

· иметь возможность наглядного представления исходных данных;

· упростить счет и интерпретацию полученных выводов;

· существенно сжать объем хранимой информации (без потерь в ее информативности).

Задача снижения размерности была решена статистиками с помощью различных методов [2, 3, 4, 8] и на сегодняшний день не представляет особой проблемы.

Методы минимизации описания

Пусть имеется выборка с n-ым количеством примеров и общим количеством признаков x⁽¹⁾, x⁽²⁾, …,x⁽^p) по каждому примеру равным p. Необходимо представить каждое из наблюдений в виде вектора Z некоторых вспомогательных показателей z⁽¹⁾, z⁽²⁾,…,z⁽^p’) с существенно меньшим (чем p) числом компонент p’. При этом новые (вспомогательные) признаки могут выбираться из числа исходных или определяться по какому-либо правилу по совокупности исходных признаков.

Решая эту задачу в процессе формирования нового набора признаков к ним предъявляют такие требования, как наибольшая информативность (в определенном смысле), взаимная некоррелированность, наименьшее искажение структуры множества исходных данных, максимальное исключение дублирующей информации и др. И уже, в зависимости от варианта формальной конкретизации этих требований, можно выбрать тот или иной алгоритм снижения размерности [37, 42, 91] и, как следствие, конкретный метод: метод главных компонент, факторный анализ, экстремальная группировка параметров и др. (табл. 1.3).

Таким образом, переход от характеризующего состояния или функционирования некоторой совокупности объектов исходного массива данных к существенно более лаконичному набору показателей, отобранных из некоторого числа исходных или построенных с помощью некоторого их преобразования таким образом, чтобы минимизировать связанные с этим потери в информации, и составляет сущность процесса снижения размерности.

Таблица 1.3

Типологизация задач снижения размерности

(АИ – автоинформативность, ВИ – внешняя информативность)

№		Класс и смысловая нацеленность критерия информативности; форма задания исходной информации		Название соответствующих методов
1		2		3
1		АИ: максимизация содержащейся в z⁽¹⁾,…, z⁽^p’) доли суммарной вариабельности исходных признаков x⁽¹⁾,…, x⁽^p). Описательная информация: в форме матрицы. Обучающая информация: отсутствует		Метод главных компонент [3, 8, 44]
2		АИ: максимизация точности воспроизведения корреляционных связей между исходными признаками по их аппроксимациям с помощью вспомогательных переменных z⁽¹⁾,…, z⁽^p’). Описательная информация: в форме матрицы. Обучающая информация: отсутствует		Модели и методы факторного анализа [51] и главных компонент
3		АИ: разбиение исходных признаков на группы высококоррелированных (внутри группы) переменных и отбор от каждой группы фактора, имеющего максимальную интегральную характеристику корреляционных связей со всеми признаками данной группы. Описательная информация: в форме матрицы. Обучающая информация: отсутствует		Метод экстремальной группировки параметров
4		АИ: приписывание каждому объекту O_i значений условных координат (z⁽¹⁾,…, z⁽^p’⁾) таким образом, чтобы по ним максимально точно восстанавливались заданная структура попарных описательных отношений между объектами. Описательная информация: в форме матрицы. Обучающая информация: отсутствует		Многомерное шкалирование [92]
5		АИ: максимальное сохранение заданных описательным массивом анализируемых структурно-геометрических и вероятностных свойств после его проецирования в пространство меньшей размерности. Описательная информация: в форме матрицы. Обучающая информация: отсутствует		Методы кластер-анализа, метод главных компонент
6		ВИ: минимизация ошибки прогноза значения результирующей количественной переменной по значениям описательных переменных. Описательная информация: в форме матрицы. Обучающая информация: в форме зарегистрированных на объектах O₁,…, O_n значений соответственно y₁,…, y_n результирующего количественного показателя y		Отбор существенных предикторов (описательных переменных) в регрессионном анализе [38, 40, 43]
7	ВИ: минимизация вероятностей ошибочного отнесения объекта к одному из заданных классов по значениям его описательных переменных. Описательная информация: в форме матрицы. Обучающая информация: для каждого описанного объекта указан номер класса, к которому он относится		Отбор типообразующих признаков в дискриминантном анализе
8	ВИ: максимизация точности воспроизведения заданных в “обучении” отношений объектов по анализируемому результирующему свойству. Описательная информация: в форме матрицы. Обучающая информация: в форме попарных сравнений или упорядочений объектов по анализируемому свойству		Методы латентно-структурного анализа
9	ВИ: максимизация точности воспроизведения заданных в “обучающей информации” попарных отношений объектов по анализируемому результирующему свойству. Описательная информация: отсутствует. Обучающая информация: в форме матрицы попарных сравнений		Многомерное шкалирование как средство латентно-структурного анализа

При этом если во время выбора подходящего математического инструментария для решения конкретной задачи следует исходить из типа конечных прикладных целей исследования и характера априорной и выборочной информации, то при определении математической модели (лежащей в основе выбора метода решения задачи снижения размерности) следует идти от типа прикладной задачи к характеристике состава и формы исходных данных, а затем – к смысловой нацеленности и конкретному виду подходящего критерия информативности. Это в свою очередь ведет к усложнению процесса обработки информации и появлению необходимости использования понятного и в достаточной мере простого (для исследователя) инструментария решения задач.

Кроме того, процесс снижения размерности выборки предполагает выявление факторов-детерминантов, а минимизация – ведет к сокращению количества признаков за счет “отбрасывания” незначимых. Однако утверждать однозначно, что отброшенные признаки являются незначимыми (неинформативными) или зашумляющими было бы некорректно, скорее часть из них попадает под категорию “условно незначимых”. То есть, информация, отраженная в таких признаках может быть полезна в процессе проведения исследований. Так, например, работая только с выборкой, основанной на минимальном наборе признаков, исследователь попадает в ситуацию, когда ошибка в данных может привести к изменению хода исследования, к снижению качества решения задач и, как следствие, к неверному решению задачи.

Описанные выше математические методы конструирования выборки в полной мере подпадают под определение распознавания образов.

Методы теории распознавания образов

Распознаванием образов называются задачи построения и применения формальных операций над числовыми или символьными отображениями объектов реального или идеального мира, результаты которых отражают принадлежность объектов к каким-либо классам, рассматриваемым как самостоятельные единицы. Существует ряд специфических, но наиболее распространенных и чаще всего применяемых методов этой группы [15, 45, 46, 47, 50].

Основываясь на способах предоставления знаний [48, 82, 97, 98], можно выделит две основные группы формальных методов распознавания образов:

1. Интенсиональные методы, основанные на операциях с признаками.

2. Экстенсиональные методы, основанные на операциях с объектами.

Особенностью интненсиональных методов является то, что в качестве элементов операций при построении и применении алгоритмов распознавания образов используются различные характеристики признаков и их взаимосвязи (табл. 1.4). При этом объекты не рассматриваются как целостные информационные единицы, а выступают в роли индикаторов для оценки взаимодействия.

Экстенсиональные методы позволяют в большей или меньшей степени придавать самостоятельное диагностическое значение каждому изучаемому объекту, поэтому основными операциями в распознавании образов с помощью данных методов являются операции определения сходства и различия объектов [105, 106]. В зависимости от условий задачи эти методы делятся на подклассы (табл. 1.5).

Таблица 1.4

Характеристика групп методов распознавания образов, основанных на операциях с признаками

Название	Характеристика	Недостатки
1	2	3
Методы, основанные на оценках плотностей распределения значений признаков [2, 100]	Объекты рассматриваются как реализация многомерной случайной величины, распределенной в пространстве признаков по определенному закону. Методы базируются на “бейсовской” схеме принятия решений и сводятся к определению отношения правдоподобия в различных областях многомерного пространства признаков	Необходимость запоминания всей обучающей выборки для вычисления оценок локальных плотностей распределения вероятностей, высокая чувствительность непредставительности выборки
Лингвистические (структурные) методы [16, 99, 108]	Основаны на использовании специальных грамматик, порождающих языки, с помощью которых может описываться совокупность свойств распознаваемых образов	Зависимость от трудности формализации грамматик по некоторому множеству описаний объектов
Методы, основанные на предположениях о классе решающих функций [16, 41, 53, 71, 96, 101]	На основании известного общего вида решающей функции и заданного функционала ее качества по обучающей последовательности ищется наилучшее приближение этой функции	Т.к. задача распознавания определяется как задача поиска экстремума, то качество ее решения полностью зависит от выбранного подхода
Логические методы [2, 14, 34, 63, 93]	Базируются на аппарате алгебры логики и позволяют оперировать информацией, заключенной в сочетаниях значений признаков. Это поиск по обучающей выборке логических закономерностей и формирование системы логических решающих правил	Требуют высокоэффективную организацию вычислительного процесса, хорошая работа возможна при небольших размерностях пространства признаков

В практике статистического анализа и моделирования, как правило, точный вид закона распределения анализируемой генеральной совокупности бывает неизвестен. Исследователь вынужден строить свои выводы на базе расчета ограниченного ряда выборочных характеристик. Кроме того, осмысленное и обоснованное использование в статистическом анализе основных выборочных характеристик требует знания их свойств, учета специфики генеральной совокупности и т.п.

Таблица 1.5

Характеристика групп методов распознавания образов, основанных на операциях с объектами

Название	Характеристика	Недостатки
Методы сравнения с прототипом [60, 81]	Применяется когда распознаваемые классы отображаются в пространстве признаков компактными геометрическими группировками. Для классификации неизвестного объекта находится ближайший прототип, и объект относится к классу прототипа	Сложности в выборе меры близости и анализе многомерных структур экспериментальных данных в условиях высокой размерности пространства признаков
Метод ближайших соседей [2, 41]	При классификации неизвестного объекта к нему находится заданное количество геометрически ближайших в пространстве признаков объектов с известной принадлежностью к распознаваемым классам, а решение об отнесении к тому или иному классу принимается путем анализа информации об этой неизвестной принадлежности его ближайших соседей	Сложности в выборе метрики для определения близости диагностируемых объектов, особенно в условиях высокой размерности пространства признаков
Алгоритмы вычисления оценок (голосования) [46, 47, 85]	Принцип действия алгоритмов вычисления оценок состоит в вычислении приоритетов (оценок сходства), характеризующих “близость” распознаваемого и эталонных объектов по системе ансамблей признаков, представляющей собой систему подмножеств заданного множества признаков	Трудности на этапе настройки алгоритмов и организации эффективного вычислительного процесса, и необходимость введения дополнительных ограничений и допущений

Вторая задача, возникающая перед исследователем в процессе обработки исходных данных – лаконичность в описании интересующих свойств исследуемой совокупности, то есть представление множества обрабатываемых данных в виде сравнительно небольшого числа сводных характеристик, построенных на основании этих исходных данных.

При этом важно, чтобы потеря информации, необходимой для принятия решений, была минимальной. Добиться лаконичности в описании информации, содержащейся в массиве обрабатываемых данных, помогает ряд прикладных методов математической статистики [1, 11]:

· выбор и обоснование математической модели механизма явления,

· изучение свойств анализируемой системы или механизма функционирования с помощью небольшого числа сводных характеристик,

· визуализация исходных данных с помощью формирования рабочих гипотез о механизме изучаемого явления, анализа относительных частот, выборочных функций распределения и других методы описательной статистики,

· анализ природы обрабатываемых данных,

· описание связей между анализируемыми признаками и т.д.

Таким образом, учитывая все эти тонкости описанных методов обработки информации, можно сказать, что с их помощью не только сложно сформировать выборку и обработать информацию, но и на начальном этапе грамотно сформулировать задачу, для дальнейшего выбора соответствующих методов анализа. Поэтому возникает задача использования таких методов, которые требовали бы минимум времени, усилий и знаний со стороны исследователя.

Развитие научно-технического прогресса привело к появлению достаточно простых инструментов, способных в комплексе решать большинство как основных, так и прикладных задач проводимых исследований. К универсальным инструментам такого рода можно отнести нейросетевые технологии, созданные на базе искусственного интеллекта.

1.3. Возможности нейросетевых подходов обработки информации

Термин искусственный интеллект (artificial intelligence) был предложен в 1956 году на семинаре в Станфордском университете в США. И вскоре произошло разделение на два основных направления: нейрокибернетику и кибернетику “черного ящика”. Но в настоящее время можно отметить тенденции к объединению этих частей в единое целое [9, 12, 20, 29, 83, 90, 104].

Основная идея нейрокибернетики заключается в следующем – единственный объект, способный мыслить, - это человеческий мозг, поэтому создаваемое “мыслящее” устройство должно каким-то образом воспроизводить его структуру. Поэтому усилия нейрокибернетики сосредоточены на создании элементов, аналогичных нейронам, и их объединения в функционирующие системы. Эти системы принято называть нейронными сетями (нейросетями).

Нейросетевые подходы к обработке информации не требуют готовых алгоритмов и правил обработки – система должна “уметь” самостоятельно вырабатывать правила и модифицировать их в процессе решения конкретных задач обработки информации [83, 87]. В настоящее время применяются три подхода к созданию нейронных сетей [27, 29, 33, 55]:

· аппаратный подход – создание специальных компьютеров, плат расширения, наборов микросхем, реализующих все необходимые алгоритмы;

· программный подход – создание программ и инструментариев, рассчитанных на высокопроизводительные компьютеры;

· гибридный подход – комбинация первых двух. Часть вычислений выполняют специальные платы расширения, а часть – программные средства.

В основу кибернетики “черного ящика” лег принцип: не имеет значения, как устроено “мыслящее” устройство, главное, чтобы на заданные входные воздействия оно реагировало так же, как и человеческий мозг [79]. Это направление искусственного интеллекта ориентировано на поиск алгоритмов решения интеллектуальных задач на существующих моделях компьютеров. В рамках этого направления были созданы и апробированы различные направления: модель лабиринтного поиска (в конце 50-х гг.); эвристическое программирования (начало 60-х гг.); модели с подключением методов математической логики (1963 – 1970 гг. и в 1973 г. создается язык Пролог); представление знаний (экспертные системы (70-е гг.)).

С одной стороны, интерес к нейросетевым моделям вызван желанием понять принципы работы нервной системы, с другой - с помощью таких моделей ученые моделируют эффективные процессы обработки информации, свойственные живым существам [46, 106].

Искусственной нейронной сетью называют некоторое устройство, состоящее из большого числа простых параллельно работающих процессорных элементов – нейронов, соединенных адаптивными линиями передачи информации – связями или синапсами. У нейронных сетей выделяют группу входных связей, по которым она получает информацию из внешнего мира, и группу выходных связей, с которых снимаются выдаваемые сетью сигналы. Нейросети применяются для решения различных задач классификации и прогнозирования и обладают рядом преимуществ перед традиционными способами обработки информации [32, 33, 35, 54, 57].

Несмотря на существенные различия алгоритмов реализации нейросетевых имитаторов, отдельные типы нейронных сетей обладают несколькими общими чертами [26, 52, 107]:

· основу каждой нейронной сети составляют относительно простые элементы, имитирующие работу нейронов мозга - нейроны. Каждый нейрон обладает группой синапсов – однонаправленных входных связей, соединенных с выходами других нейронов, а также имеют аксон – выходную связь данного нейрона, с которой сигнал поступает на синапсы следующих нейронов. Каждый синапс характеризуется величиной синаптической связи или ее весом.

· они обладают принципом параллельной обработки сигналов, который достигается путем объединения большого числа нейронов в так называемые слои и соединения определенным образом нейронов различных слоев, а также, в некоторых конфигурациях, и нейронов одного слоя между собой, причем обработка взаимодействия всех нейронов ведется послойно.

Выбор структуры нейронной сети осуществляется в соответствии с особенностями и сложностью задачи. Однако все нейронные сети состоят из взаимосвязанных клеточных автоматов.

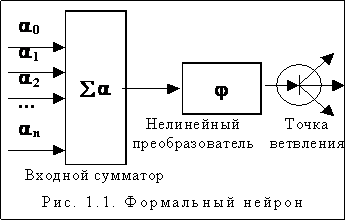Нейрон – элемент (рис. 1.1), преобразующий входной сигнал по функции: , где x - входной сигнал, c - параметр, определяющий крутизну графика пороговой функции, а c_m - параметр спонтанной активности нейрона.

Сумматор – элемент (рис. 1.2), осуществляющий суммирование сигналов поступающих на его вход:

Нелинейный преобразователь сигнала (рис. 1.3) – получает скалярный входной сигнал x и переводит его в (x).

Синапс - элемент, осуществляющий линейную передачу сигнала (рис 1.4): , где w - “вес” соответствующего синапса. Линейная связь на синапс отдельно от сумматоров не встречается, он умножает входной сигнал x на “вес синапса”.

Точка ветвления служит для рассылки одного сигнала по нескольким адресам (рис. 1.5). Она получает скалярный входной сигнал x и передает его всем своим выходам.

Среди нейронных сетей выделяют две базовые архитектуры – слоистые и полносвязные сети. Наиболее распространенными сетями для решения задач в процессе обработки информации являются слоистые нейронные сети, в которых нейроны расположены в несколько слоев (рис. 1.6). Нейроны первого слоя получают входные сигналы, преобразуют их и через точки ветвления передают нейронам второго слоя. Далее работа по слоям осуществляется аналогичным образом до того слоя, который выдает выходные сигналы. Более же подробно познакомиться со структурой и работой нейронных сетей можно в различных литературных источниках, посвященных нейроинформатике [27, 32, 104, 109].

Используя нейроимитатор для обработки информации, составить обучающую выборку для прогнозирования и диагностики не очень сложно – для этого достаточно взять намного больше признаков, а нейроимитатор потом самостоятельно расклассифицирует их по важности и (при необходимости) автоматическим путем можно будет сократить этот набор.

Прежде, чем приступить к работе с нейронной сетью исследователю, необходимо создать задачник или базу данных (обучающую выборку). Такая база обычно формируется в виде таблицы и состоит из некоторого количества примеров, обладающих многими свойствами и особенностями (признаками) и, в зависимости от задачи, имеющих результат (результаты) вычисления по каждому примеру. В свою очередь признаки могут носить различный характер и быть: существенными и второстепенными; качественными и количественными; первичными и вторичными и т.д. [30, 39, 64, 72, 73]. При этом для работы с нейронной сетью (опять же в зависимости от поставленной задачи) к выборке не предъявляется такое количество жестких требований, как, например, при работе с традиционными методами обработки информации. Структура таблицы экспериментальных данных приведена в табл. 1.6.

Таблица 1.6

База данных

Объекты	Исходные признаки						Результаты
Объекты	x₁	x₂	…	x_j	…	x_M	Y₁	…	Y_P
X¹	x¹₁	x¹₂	…	x¹_j	…	x¹_M	Y¹₁	…	Y¹_P
X²	x²₁	x²₂	…	x²_j	…	x²_M	Y²₁	…	Y²_P
…	…	…	…	…	…	…	…	…	…
Xⁱ	xⁱ₁	xⁱ₂	…	xⁱ_j	…	xⁱ_M	Yⁱ₁	…	Yⁱ_P
…	…	…	…	…	…	…	…
X^N	x^N₁	x^N₂	…	x^N_j	…	x^N_M	Y^N₁		Y^N_P

Такая таблица содержит N примеров, для характеристики которых используется некоторое количество признаков (равное M) и по заранее известному количеству результатов (равное P).

Для формирования такой таблицы необходимо обратить внимание на количество примеров (чем их больше, тем точнее результат вычисления); на информативную загрузку набора признаков: для начала работы лучше взять, как можно больше признаков (в последствии этот набор можно будет сократить), при этом их количество ограничивается лишь возможностями программного обеспечения.

Нейронная сеть способна обучаться решению задачи на основании такой обучающей выборки – "задачника", состоящего из набора пар "вход–требуемый выход", и далее может решать примеры, не входящие в обучающую выборку [75, 88]. При этом процесс обучения представляет собой автоматический поиск закономерности между данными и заранее известным результатом в обучающей выборке. Примеры из предложенной выборки предъявляются нейросетевой модели, а нейроны, получая по входным связям сигналы - "условия примера", преобразуют их, несколько раз обмениваются преобразованными сигналами и выдают ответ (набор сигналов) [21, 24, 25, 28, 36].

Обученная нейронная сеть автоматически записывается на диск компьютера как обыкновенный файл. В любой момент времени можно считать сеть с диска и продолжить обучение со старой или новой обучающей выборкой. Одна нейронная сеть обучается решать только одну задачу, однако может использовать для обучения различные обучающие выборки. Которые могут различаться по количеству примеров, но должны соответствовать друг другу по числу обучающих параметров и их порядку и смыслу.

Тестирование выборки с заранее известными результатами позволяет проверить, правильно ли сеть определяет результаты для всех примеров и насколько уверенно она это делает. Полученный результат по каждому примеру сравнивается с заранее известным, и если сеть обучилась полностью, то при тестировании той же самой выборки результаты будут определены правильно.

Кроме такого алгоритма тестирования можно так же протестировать выборки с примерами, которые не участвовали в обучении нейронной сети. В этом случае можно спрогнозировать неизвестный результат или выявить недостатки в обучающей выборке, в структуре сети и в постановке задачи.

Изменяя в различных направлениях значения параметров примера и повторяя его тестирования, можно определить, как и на сколько изменяется значение результата. Это позволяет создать почву для составления рекомендаций по изменению результата в реальной жизни.

В процессе обучения нейронная сеть способна оценивать влияние каждого из обучающих параметров на принятие решения (то есть определить степень важности отдельных признаков). Эта способность позволяет выявить информативность каждого признака по сравнению с остальными и оценить значимость признаков [22, 23, 89, 102].

Применение этих алгоритмов и вычисленные на их основе показатели значимости признаков позволяют анализировать вектор входных сигналов на избыточность. То есть, отбрасывая сигналы, показатель которых имеет маленькое значение для вычисления ответа, обучаем сеть без него и смотрим изменение ошибки. В том случае, когда значение ошибки укладывается в заданный интервал, таким признаком можно пренебречь (исключить из выборки), а когда результат вычисляется более точно, можно говорить о зашумлении выборки этим признаком.

Данная возможность нейронных сетей (оценка значимости признаков) позволяет решить еще одну проблему: облегчение процесса создания вопросника для решения конкретной задачи. То есть для начала можно сформировать обучающую выборку с большим количеством признаков, а затем нейроимитатор способен сам расклассифицировать их по важности и сократить список входных сигналов.

С помощью нейронных сетей можно автоматически минимизировать число обучающих признаков [31]. При этом сокращение множества параметров и входных сигналов нейросети может преследовать несколько целей [54]:

· упрощение специализированных технических устройств;

· сокращение объема используемой памяти и увеличение быстродействия нейросети при решении задачи;

· удешевление и упрощение сбора данных за счет отбрасывания наименее значимых;

· облегчение явной вербальной интерпретации процесса и результатов обработки данных.

Алгоритмы минимизации пространства признаков рассмотрены в книге Горбаня А.Н. и Россиева Д.А. “Нейронные сети на персональном компьютере”, а также в материалах III Всероссийского семинара “Нейроинформатика и ее приложения”.

Одними из исследователей, занимающихся теоретическими вопросами в области нейроинформатики и разрабатывающих программное обеспечение для решения прикладных задач в этой области, являются члены группы НейроКомп Красноярского института вычислительного моделирования СО РАН [76, 77]. Ими был разработан пакет MultiNeuron, который состоит из трех программ и является программным инструментарием, позволяющим создавать экспертные системы, и NeuroPro.

Последний программный продукт представляет собой менеджер обучаемых искусственных нейронных сетей, работающий в среде MS Windows 95 или MS Windows NT 4.0. В процессе работы NeuroPro позволяет производить следующие базовые операции:

1. Создание нейросетевого проекта.

2. Подключение к нейропроекту файла (базы) данных в формате dfb (dBase, FoxBase, FoxPro, Clipper) или db (Paradox).

3. Редактирование файла данных – изменение существующих значений, добавление новых записей в базу данных и сохранение файла данных в другом формате.

4. Добавление в проект нейронной сети слоистой архитектуры с числом слоев нейронов от 1 до 10, числом нейронов в слое – до 100.

5. Обучение нейронной сети решению задачи прогнозирования или классификации. Нейронная сеть может одновременно решать как несколько задач прогнозирования, так и несколько задач классификации, а также одновременно задач и прогнозирования, и классификации.

6. Тестирование нейронной сети на файле данных, получение статистической информации о точности решения задачи.

7. Вычисление показателей значимости входных сигналов сети, сохранение значений показателей значимости в текстовом файле на диске.

8. Упрощение нейронной сети.

9. Генерация и визуализация вербального описания нейронной сети, сохранение вербального описания в текстовом файле на диске.

10. Выбор алгоритма обучения, назначение требуемой точности прогноза, настройка нейронной сети.

По мнению авторов, данный продукт отличает наличие возможностей целенаправленного упрощения нейронной сети для последующей генерации вербального описания. В дальнейшем все эксперименты по данной диссертационной работе будут проводиться именно с помощью нейросетевого имитатора NeuroPro.

Интеллектуальные системы на основе искусственных нейронных сетей позволяют с успехом решать проблемы распознавания образов, выполнения прогнозов, оптимизации, ассоциативной памяти и управления [96, 109]. Они предпочтительны там, где имеется очень много входных данных, в которых скрыты закономерности. В этом случае можно почти автоматически учесть различные нелинейные взаимодействия между показателями-признаками, характеризующими такие данные. Это особенно важно в системах обработки информации, в частности, для ее предварительного анализа или отбора, выявления "выпадающих фактов" (условно незначимых признаков) или грубых ошибок человека, принимающего решения [12, 32, 103, 110].

Таким образом, имея достаточно простой набор элементов структуры, нейронные сети способны решать разнообразные задачи: а) управление в реальном времени; б) распознавание образов; в) предсказание; г) оптимизация; д) задачи обработки сигналов при наличии больших шумов и т.д. И можно сказать, что нейронные сети универсальный инструмент, с точки зрения исследователя они являются достаточно производительными и зависят лишь от производительности вычислительной машины, они обеспечиваю достаточно высокую устойчивость к ошибкам, на сегодняшний день они являются дешевым продуктом. В итоге получаем, что применять технологии нейронных сетей выгодно, а разработка методов нейросетевого моделирования и анализа информации является актуальной задачей.

1.4. Оценка качества решения задач и виды контроля достоверности данных

Характеристика рассмотренных выше подходов и методов обработки информации была бы не полной без учета оценки качества алгоритмов и способов определения критериев таких оценок. Показателями качества обычно являются ошибки вычислений (классификации), либо связанные с ними некоторые функции потерь. При этом ошибки бывают: условно-вероятностными, ожидаемыми и асимптотическими, а функции потерь разделяют на: функцию средних потерь, функцию ожидаемых потерь и эмпирическую функцию средних потерь [2, 6].

Способы оценки того или иного показателя качества делятся на три основные экспериментальные группы:

1. Одновременное использование выборки как обучающей и контрольной. Этот способ дает завышенную оценку качества решения задачи по сравнению с оценкой качества по не зависимым от обучения данным.

2. Разбиение выборки на две части – обучающую и контрольную. Данный способ применяется в экспериментах с достаточно большим количеством данных и является самым простым и наиболее убедительным.

3. Извлечение из выборки случайного объекта (контрольного), синтез решающего правила по оставшимся и распознавание извлеченного объекта. Данный способ получил название метод скользящего экзамена и является наиболее предпочтительным, так как дает меньшую дисперсию оценки вероятности ошибки.

Выбор способа оценки полностью зависит от поставленных перед исследователем задач. Однако хотелось бы обратить внимание на то, что точность решения задачи зависит не только от выбранной модели и ее способности, но и от точности исходных данных. При этом если модель поддается изменению и адаптации, то ошибки в данных – это проблема, плохо поддающаяся решению.

Как правило, ошибки в данных носят преднамеренный и неумышленный характер и возникают по вине исследователя. Преднамеренные искажения данных проявляются систематически, а методы борьбы с ними носят организационный характер применительно к человеку.

Методы борьбы же с искажениями, возникающими из-за невнимательности, случайности, усталости и т.п., рассматривались до сих пор учеными только в рамках контроля достоверности данных (табл. 1.7) [80].

В условиях роста информационных потоков и применения компьютерной техники специфика обработки данных ведет к появлению таких операций как кодирование признаков и перенос данных с первичных документов на машинные носители. И в этих условиях проблема появления искажений информации и на сегодняшний день имеет свою актуальность (особенно при работе с выборкой, основанной на минимальном количестве признаков).

Таблица 1.7

Виды и содержание контроля

Способы контроля	Что проверяется?
Синтаксический (вручную)	Структура документа Полнота документа Полнота заполнения строк
Логический (на ЭВМ)	Соответствие кодов и наименований признаков Наличие отклонений от заданных значений Наличие логических связей между показателями
Арифметический (на ЭВМ)	Соответствие построчных контрольных сумм документа и контрольных сумм ЭВМ Соответствие пографных сумм документа и контрольных сумм ЭВМ

Применение различных видов контроля достоверности данных хоть и является действенным, но и здесь не исключена возможность появления искажений информации. Поэтому на сегодняшний день нет способов, способных существенно повлиять на качество решения задач в ситуациях с искажениями во входных данных.

В связи с этим, в процессе решения задач минимизации пространства признаков в условиях возникновения искажений информации, возникает проблема поиска компромисса, способного реализовать и цели минимизации и цели повышения устойчивости систем обработки данных от такого рода ошибок.

1.5. Дублирование информации – источник повышения устойчивости вычислительных систем к искажению входной информации

Решение задачи создания системы, устойчивой к искажениям входной информации на выборке с минимальным количеством признаков можно строить по двум направлениям.

Первое направление - “сверху вниз”. То есть, путем отбрасывания наименее значимых признаков из исходной выборки и постоянным контролем над устойчивостью системы (изменением ошибки вычислений) к искусственно создаваемым искажениям во входной информации. Однако данный подход ведет к тому, что решение задачи минимизации будет неудовлетворительным (то есть, в процессе реализации данного подхода говорить о “минимуме” практически невозможно).

Второе направление - “снизу вверх”. То есть, изначально сократить набор исходных признаков до минимального количества, а затем увеличивать минимальное количество признаков такими признаками (из множества не вошедших в минимальный набор), которые повышали бы устойчивость системы к искажениям информации во входных данных. Реализация этого направления требует перебора как минимум всех “оставшихся” признаков и постоянного контроля над качеством вычислений в условиях искажения информации.

Таким образом, эти подходы являются достаточно трудоемкими и заранее ведут к избыточному увеличению количества входных параметров. Поэтому очевидно, что решать поставленную задачу необходимо с помощью такого метода, который позволил бы за меньшее количество итераций определять набор признаков, повышающих устойчивость системы к искажениям информации в условиях сокращения исходного числа входных параметров. В роли такого метода выступает предлагаемый ниже метод дублирования информации. Его теоретическому описанию и реализации при решении задач прогнозирования и классификации посвящены данные диссертационные исследования.

Понятие “дублирование информации” рассматривается в литературе как “…одна из предпосылок, обуславливающих необходимость перехода от большого числа исходных показателей состояния анализируемой системы к существенно меньшему числу наиболее информативных переменных” [2, 3]. Однако для построения систем, обладающих устойчивостью к искажениям во входных данных, дублирование информации может сыграть существенную роль. Суть идеи применения дублирующей информации состоит в том, чтобы создавать устойчивость системы путем дополнения минимального набора признаками-дублерами [17, 18]. При этом дублировать можно как весь минимальные набор, так и отдельные признаки из его состава, а преимущество состоит в том, что исследователь определяет непосредственные признаки-дублеры за минимальное количество итераций, а не создает устойчивость системы к искажениям во входных данных посредством перебора признаков.

Этот способ создания устойчивости системы к искажениям во входных данных путем дублирования информации из минимального набора признаков позволит решить следующие задачи.

1. Дублирование информации из минимального набора признаков позволит избежать потери части полезной информации, или информации, которая в процессе реализации методов минимизации перешла в разряд относительно незначимой, и сократить ограничения в использовании дополнительных априорных сведений о решаемой целевой задаче.

2. Решение задачи, основанное на минимальном наборе признаков, сопряжено с высокой степенью риска возникновения ошибок вычислений в случаях невнимательности исследователя (неумышленных искажений в данных). Увеличивая же минимальный набор признаков соответствующими дублирующими признаками, вероятность искажений во всех данных сокращается, отсюда снижается степень риска и повышается качество решения задачи.

3. Наличие в выборке признаков, дублирующих информацию из минимального набора, позволяет повысить качество вычислений в условиях наличия пробелов в данных. А при соответствующей аппаратной поддержке и восполнить эти пробелы с достаточной степенью достоверности.

4. На базе построенных наборов признаков (полном, дублирующем и минимальном) выстраивается иерархическая зависимость между наборами, что позволяет исследователю выбирать одну из трех баз данных в зависимости от критериев, предъявляемых к решению задачи и от технического и инструментального обеспечения.

Таким образом, решение задачи сводится к поиску признаков, дублирующих информацию из минимального набора параметров, и созданию алгоритмов формирования наборов повышающих надежность вычислительных моделей. Под надежностью в дальнейшем будем понимать устойчивость системы (в данном случае нейросетевой) к искажениям информации во входных данных.

Выводы к главе 1

1. Проведенный анализ процесса информатизации общества показал, что вопросы отбора, анализа, обработки и использования информации на сегодняшний день являются актуальными и специфическими, а роль и значение исследователя на всех этапах ее прохождения наиболее существенными для качественного решения поставленных задач.

2. Анализ особенностей использования традиционных методов и инструментов обработки информации показал, что алгоритмы их реализации не удовлетворяют требованиям сокращения времени, усилий и количества специализированных знаний со стороны исследователя. Однако в качестве универсального инструмента обработки информации и минимизации описания выступает нейросетевой подход к обработке данных.

3. Анализ различных способов контроля достоверности данных показал, что в процессе решение задач минимизации пространства признаков в условиях возникновения неумышленных искажений информации, возникает проблема поиска компромисса, способного реализовать и цели минимизации и цели сохранения устойчивости систем обработки данных от таких ошибок.

4. Проведен анализ различных подходов к решению задачи поиска набора входных параметров, обеспечивающих устойчивость решения к искажениям во входной информации. На его основе предложен метод дублирования, основанный на увеличении количества признаков минимального набора на число соответствующих признаков с дублирующей информацией.

ГЛАВА 2. ДУБЛИРОВАНИЕ ПРИЗНАКОВ КАК СРЕДСТВО ПОВЫШЕНИЯ НАДЕЖНОСТИ В ПРОЦЕССЕ ОБРАБОТКИ ИНФОРМАЦИИ

2.1. Формализация основных понятий и классификация дублей

Реализация решения вышеизложенных задач основана на увеличении пространства признаков - добавлении к минимальному набору такого набора признаков, который если не полностью, то частично дублирует информацию из минимального набора, то есть формируется набор, способный минимизировать степень влияния неумышленных искажений информации. Теоретически задача и ее решение выглядят следующим образом.

Рассмотрим обучающую выборку V (см. табл. 1.6), в которой n - общее количество объектов, m - количество признаков по каждому объекту, а p- количество результатов каждого объекта.

Пусть данная выборка является совокупностью однородных объектов характеризующихся некоторым числом качественных и количественных признаков и результатов. Определим целевую задачу, – в процессе работы с данной выборкой необходимо спрогнозировать результат так, чтобы отклонение вычисленного значения результата от существующего (заданного) было как можно меньше и укладывалось в пределы заданной точности вычислений. И, плюс к этому, необходимо сократить размерность вектора входных признаков с учетом вышеизложенного требования и возможности возникновения искажений информации.

Не будем акцентировать внимание на способах прогнозирования результата, так как решение этого вопроса описано во многих литературных источниках. Отметим лишь, что в рамках решения этой задачи воспользуемся имитатором нейронных сетей “NeuroPro” [76, 77], который позволяет достаточно быстро решать задачи прогнозирования результатов, оценки информативности параметров и, что очень важно, автоматически минимизировать число входных характеристик. (Однако следует заметить, что предложенные ниже алгоритмы поиска дублирующих признаков необязательно базируются на использовании нейронных сетей.)

Решение следующей подзадачи минимизации описания позволяет повысить вычислительную эффективность соответствующих алгоритмов и имеет самостоятельное значение [46]. Известно, что процесс минимизации общего количества признаков основан на вычислении информативности каждого из них [58, 86]. То есть, определяется значимость каждого признака в обучающей выборке, отбрасываются наименее информативные из них, и создается новая выборка S` с вектором входных признаков меньшей размерности (табл. 2.1), где N – общее количество примеров, а M` - общее количество признаков.

Таблица 2.1

Структура выборки S`

Объекты	Исходные признаки						Результаты
Объекты	x₁	x₂	…	x_j	…	x_M_`	Y₁	…	Y_P
X¹	x¹₁	x¹₂	…	x¹_j	…	x¹_M`	Y¹₁	…	Y¹_P
X²	x²₁	x²₂	…	x²_j	…	x²_M`	Y²₁	…	Y²_P
…	…	…	…	…	…	…	…	…	…
Xⁱ	xⁱ₁	xⁱ₂	…	xⁱ_j	…	xⁱ_M_`	Yⁱ₁	…	Yⁱ_P
…	…	…	…	…	…	…	…
X^N	x^N₁	x^N₂	…	x^N_j	…	x^N_M_`	Y^N₁		Y^N_P

Как видно из таблицы 2.1 , выборка S` меньшей размерности отличается от исходной размерностью вектора входных признаков, который был сокращен до некоторого числа M` < M без существенной потери качества прогнозирования результата.

Однако нельзя утверждать, что отброшенные признаки не имеют значения для решения поставленной задачи, а их информативность является наименьшей. Корректнее всего было бы рассматривать понятие “условно незначимые” признаки. Тогда возникает вопрос: насколько хорош созданный минимальный набор параметров?

В зависимости от решаемой задачи ответ на этот вопрос может быть разным. Если все входные параметры являются объективными (например, результатами физических измерений), то минимальный набор входных параметров видимо надежен. Однако если входные параметры являются субъективными, минимальный набор не надежен, а принятое решение на основе минимального набора таких субъективных признаков некорректно. И, кроме того, нельзя забывать и об неумышленных ошибках в данных.

Прежде, чем приступить непосредственно к описанию метода и алгоритмов реализации, введем понятие “дубля”. Для начала обратимся к понятиям прототип и дублер:

· “прототип” – начальный, основной образец, источник;

· “дублер” – это двойник, способный почти полностью компенсировать отсутствие прототипа.

Таким образом “дубль” – это набор дублеров, а “дублирование” - это процесс замены прототипа(ов) соответствующим(ими) дублером(ами).

Можно предложить множество видов дублей в зависимости от направления дублирования, например:

· дубль для всех признаков из минимального набора;

· дубль для части признаков (в диссертационной работе не рассматривается);

· дубль для одного конкретного признака;

· дубль на основе замены признака (совокупности признаков);

· дубль на основе вычислений значения признака (совокупности значений признаков) и т.д.

В целях ограничения диссертационных исследований остановимся на реализации “крайних состояний”. В связи с этим классифицируем дубли по двум принципам: по объекту дублирования и по способу определения.

Классификация дублей

1. По объекту дублирования:

· дубль первого рода - такой дубль позволяет дублировать все множество признаков из минимального набора в целом;

· дубль второго рода – позволяет дублировать конкретный признак (прототип).

2. По способу определения:

· прямой дубль – набор признаков, способный заменить определенный признак (или множество признаков) при получении ответа первоначальной задачи;

· косвенный дубль - и набор признаков, позволяющий вычислить дублируемый признак (множество дублируемых признаков).

Исходя из предложенной классификации очевидно, что возможны четыре варианта дублей (рис. 2.1): прямой дубль первого рода, косвенный дубль первого рода, прямой дубль второго рода, косвенный дубль второго рода.

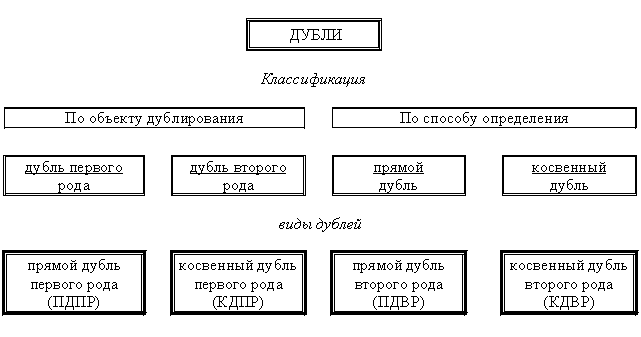
Рис. 2.1. Классификация и разновидности дублей

Задача. Пусть дана таблица данных, содержащая n записей, каждая из которых содержит M+P+1 поле. Введем соответствующие обозначения:

1. Обозначим значение каждого j-го поля i-ой записи через xⁱ_j, где i=1,…,N, j=1,…,M.

2. Обозначим через V(A,S) задачник, в котором ответы заданы в полях с номерами jÎA, а входные данные содержатся в полях с номерами jÎS. Множество А будем называть множеством ответов, а множество S – множеством входных данных.

3. Минимальное множество входных сигналов, полученное при обучении сети на задачнике V(A,S), обозначим через F(A,S).

4. В случае, когда сеть не удалось обучить решению задачи, будем считать, что F(A,S)=Æ.

5. Число элементов во множестве A будем обозначать через ½A½.

6. Через T(A,S) будем обозначать сеть, обученную решать задачу предсказания всех полей (ответов), номера которых содержатся в множестве A, на основе входных сигналов, номера которых содержатся в множестве S.

Необходимо построить набор входных параметров, который позволяет надежно решать задачу V({0},{1,…,M}).

Решение задачи будем называть множеством повышенной надежности, и обозначать S_пн.

Для решения этой задачи необходимо определить набор параметров, дублирующих минимальный набор S₁=F({0}, {1,…,M}).

Рассмотрим последовательно алгоритмы поиска дублей всех вышеперечисленных видов и процессы формирования наборов повышенной надежности на основе предложенной классификации.

2.2. Алгоритмы дублирования

2.2.1. Прямой дубль первого рода (ПДПР)

Для нахождения прямого дубля первого рода требуется найти такое множество признаков D из множества M``= M-M`, которое является минимальным для решения задачи прогнозирования результата. При этом необходимо выполнение условия, что существует сеть T({0},D) и S₁|D=Æ. Алгоритм решения этой задачи приведен на рис. 2.2.

Рис. 2.2. Процесс формирования ПДПР и набора повышенной надежности

Определим минимальное множество признаков (M`), необходимое для вычисления результата. Затем исключим из общего множества входных признаков M те из них, которые вошли в первоначальное минимальное множество признаков S₁(то есть M-M`). Следующим шагом найдем минимальное множество признаков среди оставшихся признаков (M``). Это множество и будет искомым дублем.

Формально описанную выше процедуру можно записать следующей формулой:

D=F({0},{1,…,M}\S₁).

При этом множество повышенной надежности в этом случае можно записать в следующем виде:

S¹ⁿ_пн= S₁ U D=F({0},{1,…,M}) U F({0},{1,…,M}\ F({0},{1,…,M})).

Очевидно, что последнюю формулу можно обобщить, исключив из первоначального множества признаков найденное ранее множество повышенной надежности и попытавшись найти минимальное множество среди оставшихся признаков. Однако можно выделить круг таких задач, для которых не существует прямых дублей первого рода. Примером может служить одна из классических нейросетевых тестовых задач – задача о предсказании результатов выборов президента США.

2.2.2. Косвенный дубль первого рода (КДПР)

Для нахождения косвенного дубля первого рода необходимо найти такое множество признаков D из множества M``= M-M`, которое является минимальным и позволяющим вычислить дублируемые признаки множества M`. При этом необходимо выполнить условие, что существует сеть T({0},D) и S₁|D=Æ. Другими словами, среди множества признаков, не включающего начальное минимальное множество (M-M`), нужно найти такие признаки, по которым можно восстановить значения признаков начального минимального множества. Схематично процесс формирования косвенного дубля первого рода изображен на рис. 2.3.

Математически же описанную выше процедуру можно записать следующей формулой:

D=F(S₁,{1,…,M}\S₁).

А множество повышенной надежности в этом случае можно записать в следующем виде:

S^1к_пн= S₁ U D=F({0},{1,…,M}) U F({0},{1,…,M}){1,…,M}\ F({0},{1,…,M})).

Рис. 2.3. Процесс формирования КДПР и набора повышенной надежности

Эта формула так же допускает обобщение. Однако следует заметить, что косвенные дубли первого рода встречаются еще реже, чем прямые дубли первого рода. Соотношение между косвенным и прямым дублем первого рода можно описать с помощью следующей теоремы.

Теорема 1. Если множество D является косвенным дублем первого рода, то оно является и прямым дублем первого рода.

Доказательство. Построим нейронную сеть, состоящую из последовательно соединенных сетей T(S₁,D) и T({0},S₁) (рис. 2.4). Очевидно, что на выходе первой сети будут получены те сигналы, которые, будучи поданы на вход второй сети, приведут к получению на выходе второй сети правильного ответа. Таким образом сеть, полученная в результате объединения двух сетей T(S₁,D) и T({0},S₁), является сетью T({0},D). Что и требовалось доказать.

Рис. 2.4. Сеть для получения ответа из косвенного дубля

Из данной теоремы вытекает следующее следствие.

Следствие. Если у множества S₁ нет прямого дубля первого рода, то у нее нет и косвенного дубля первого рода.

Доказательство. Пусть это не так. Тогда существует косвенный дубль первого рода. Но по теореме 1 он является и прямым дублем первого рода, что противоречит условию теоремы. Это противоречие и доказывает следствие.

2.2.3. Прямой дубль второго рода (ПДВР)

Прежде, чем приступить к описанию процесса определения прямого дубля второго рода и косвенного дубля второго рода перенумеруем входные признаки из множества S₁={i₁,…,i_k},k=|S₁|. Тогда множество признаков, являющееся прямым дублем второго рода для признака можно получить, найдя минимальное множество для получения ответа, если из исходного множества входных признаков исключен признак . Отсюда получаем, что прямые дубли второго рода определяются следующим образом: D_j=F({0},{1,…,M}\{i_j}).

Полный прямой дубль второго рода является объединением всех дублей для отдельных признаков (рис. 2.5):

|S₁|

D=U F({0},{1,…,M}\{i_j}).

j=1

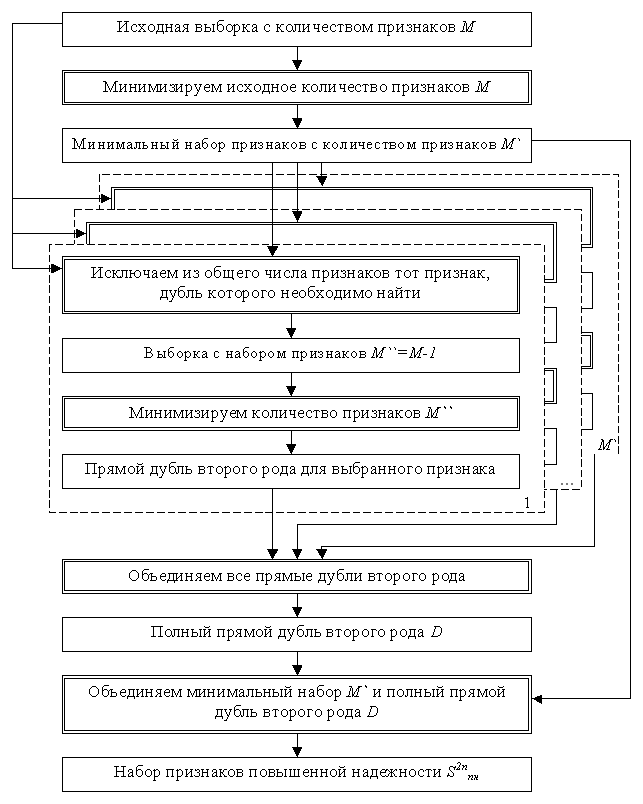
Рис. 2.5. Процесс формирования ПДВР и набора повышенной надежности

Множество повышенной надежности для прямого дубля второго рода можно записать в следующем виде:

S²ⁿ_пн= F({0},{1,…,M}) U F({0},{1,…,M}\{j}).

jÎF({0},{1,…,M})

При формировании прямого дубля второго рода, в зависимости от поставленной задачи, можно ограничиться несколькими признаками. В этом случае множество повышенной надежности будет складываться из минимального набора признаков плюс прямые дубли второго рода для интересующих исследователя признаков. Если же прямой дубль второго рода требуется найти лишь для одного признака из минимального множества, то тогда набор повышенной надежности будет состоять из минимального множества и единственного прямого дубля второго рода.

Заметим, что при построении прямого дубля второго рода не требовалось отсутствия в нем всех элементов множества S₁, как это было при построении прямого дубля первого рода. Такое снижение требований приводит к тому, что прямые дубли второго рода встречаются чаще, чем прямые дубли первого рода. Более того, прямой дубль первого рода, очевидно, является прямым дублем второго рода. Более точное соотношение между прямыми дублями первого и второго родов дает следующая теорема.

Теорема 2. Полный прямой дубль второго рода является прямым дублем первого рода тогда, и только тогда, когда

U F({0},{1,…,M}\{j})|F({0},{1,…,M})=Æ

jÎF({0},{1,…,M})

(1)

Доказательство. Построим сеть, состоящую из параллельно работающих сетей, T({0},{1,…,M}\{i_j}), за которыми следует элемент, выдающий на выход среднее арифметическое своих входов. Такая сеть, очевидно, будет решать задачу, а в силу соотношения (1) она будет сетью T({0},{1,…,M}\S₁). Таким образом, если соотношение (1) верно, то прямой дубль второго рода является прямым дублем первого рода. Необходимость следует непосредственно из определения прямого дубля первого рода.

2.2.4. Косвенный дубль второго рода (КДВР)

Косвенный дубль второго рода для признака является минимальным множеством входных признаков, для которых существует сеть T({i₁},{1,…,M}\{i₁}). Другими словами – это такое минимальное множество признаков (дублеров), по которому можно восстановить значение признака (прототипа) из минимального множества. То есть, этот признак (прототип) переводится из разряда “характеристик” в разряд “результатов”.

Таким образом, косвенные дубли второго рода получаются следующим образом: D_j=F({i_j},{1,…,M}\{i_j}) (рис. 2.6).

Полный косвенный дубль второго рода строится как объединение косвенных дублей второго рода для всех признаков первоначального минимального множества (2), а множество повышенной надежности можно выразить формулой (3).

	\|S₁\| D=U F({i_j},{1,…,M}\{i_j}). j=1	(2)

S^2к_пн= F({0},{1,…,M}) U F({j},{1,…,M}\{j}). jÎF({0},{1,…,M})			(3)

Соотношения между косвенными дублями второго рода и другими видами дублей первого и второго рода задаются теоремами 1, 2 и следующими двумя теоремами.

Теорема 3. Косвенный дубль второго рода всегда является прямым дублем второго рода.

Доказательство данной теоремы полностью аналогично доказательству теоремы 1.

Теорема 4. Полный косвенный дубль второго рода является косвенным дублем первого рода тогда, и только тогда, когда верно соотношение

U F({j},{1,…,M}\{j})|F({0},{1,…,M})=Æ

jÎF({0},{1,…,M})

Доказательство данной теоремы полностью аналогично доказательству теоремы 2.

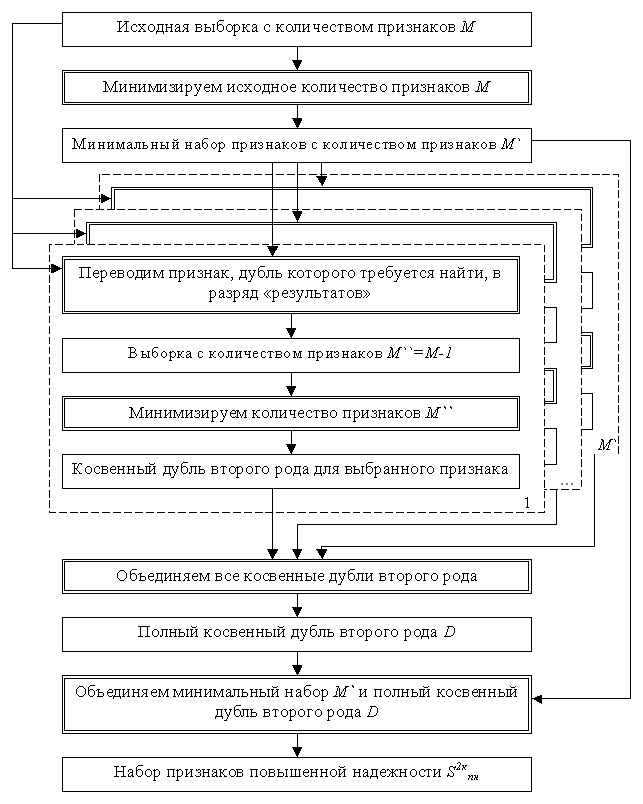
Рис. 2.6. Процесс формирования КДВР и набора повышенной надежности

2.3. Теоретические результаты дублирования

Таким образом, применяя данные алгоритмы дублирования в процессе обработки первичной информации в сочетании с нейросетевыми возможностями, исследователь получает качественно новые системы поддержки и принятия решений.

Дублирование информации позволяет сократить набор входных характеристик таким образом, чтобы качество вычисления результата минимально пострадало от искажений входной информации в процессе дальнейшей работы с выборкой. Кроме этого, набор повышенной надежности на базе косвенного дубля второго рода позволяет делать выводы о наличии ненужных (“зашумляющих”) признаков. Однако процесс определения наборов повышенной надежности на базе полных косвенного и прямого дублей второго рода является достаточно трудоемким.

Еще одной задачей, которую можно решать с помощью дублирования, является задача вычисления или прогнозирования результата на таблице данных имеющей пробелы. То есть в том случае, когда отсутствуют данные по ряду примеров, можно определить их значение с помощью соответствующих дублеров. Или же проще того, дублеры, вошедшие в набор повышенной надежности, частично заменят отсутствие информации в прототипах. Что существенно отразится на качестве принятия решения.

При решении задачи расстановки приоритетов среди признаков в выборке исследователь может воспользоваться методом дублирования информации и выстроить иерархическую зависимость признаков друг от друга. То есть, с помощью реализации алгоритмов поиска дублей (ПДПР, КДПР, ПДВР, КДВР) на высшем уровне пирамиды будут находиться признаки-прототипы из минимального набора, на среднем уровне – признаки-дублеры, а на низшем уровне – набор признаков, обладающих повышенной надежность к неумышленным искажениям информации (рис. 2.7). В основе же всей этой пирамиды будет лежать весь набор признаков.

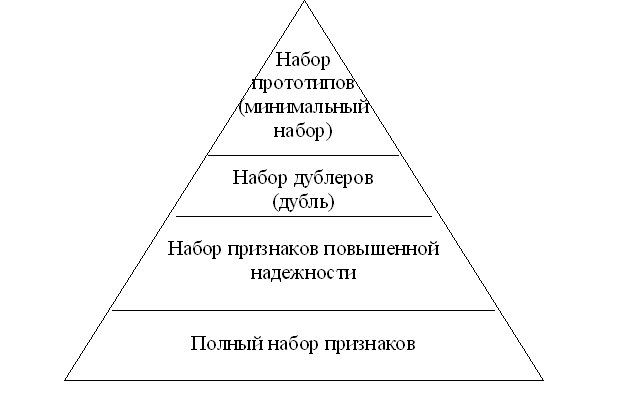
Рис. 2.7. Иерархическая структура признакового пространства для ПДПР, КДПР, ПДВР и КДВР

Такая возможность, предоставляемая методом дублирования, позволяет создавать почву для выработки дополнительной информации нового качества и структуре пространства признаков. Кроме того, при решении различного рода задач применение дублирования информации помогает исследователю формировать выборки с различным набором признаков, деленные на первичные и вторичные. Эта возможность наиболее актуальна при технических ограничениях решения задач.

Так как процесс поиска дублеров и прототипов основан на минимизации пространства признаков, то алгоритмы поиска дублирующих признаков могут быть реализованы не только с помощью нейросетевых инструментов. Выбор того или иного метода минимизации будет зависеть от поставленной задачи, знаний исследователя и возможностей необходимых технических средств.

Выводы к главе 2

1. С целью уменьшения количества признаков и одновременного повышения устойчивости решения задачи в условиях искажения входных данных предложено использование дублирования признаков минимального набора.

2. Выделено четыре вида дублей: прямой дубль первого рода, косвенные дубль первого рода, прямой дубль второго рода и косвенный дубль второго рода, различающихся по объекту дублирования и способу определения.

3. Сформулированы алгоритмы получения дублей:

- алгоритм поиска прямого дубля первого рода предполагает поиск минимального набора признаков (для вычисления результата) из множества M``=M-M`,

- косвенный дубль первого рода предполагает перевод минимального набора признаков M` в разряд результатов и поиск нового минимального набора признаков из множества M``= M-M`, способного вычислить эти результаты,

- прямой дубль второго рода и косвенный дубль второго рода получаются аналогично предыдущим, только дублирование проводят не для всего минимального множества M`, а для определенных признаков.

4. Показаны соотношения между различными видами дублей, и выявлено, что формализм описания алгоритмов может быть применен как к нейронным сетям, так и к линейной и нелинейной регрессии.

5. Одновременное использование набора прототипов и дублеров позволяет формировать набор признаков, обладающий устойчивостью к неумышленным искажениям информации.

ГЛАВА 3. ДУБЛИРОВАНИЕ В ПРОЦЕССЕ РЕШЕНИЯ ЗАДАЧИ КЛАССИФИКАЦИИ ПРЕДСКАЗАНИЙ ЛЕТАЛЬНОГО ИСХОДА В СЛУЧАЕ НАСТУПЛЕНИЯ ИНФАРКТА МИОКАРДА

3.1. Описание задачи и процесса ее решения

Для проведения исследований в данной области воспользуемся частью базы данных, опубликованной Институтом вычислительного моделирования СО РАН в 1997 году на материалах Кардиологического центра городской больницы №20 [32] и неросетевым имитатором NeuroPro.

Прежде, чем непосредственно приступить к экспериментам по формированию дублей различного рода, обратимся к имеющейся информации и определим цели исследований.

Для работы с выбранным программным продуктом на первом этапе необходимо сформировать задачник (см. табл. 1.6). В его состав вошла часть базы данных и в итоге получилась выборка из 529 примеров, 118 признаков (см. прил. 1) и одного прогнозируемого результата. При этом признаки носят в основном качественный характер, а результатом является определенный класс (см. прил. 2).

Таким образом, стоит задача соотнесения объектов выборки к определенному классу (задача классификации), сокращении числа входных сигналов, создание набора повышенной надежности к неумышленным искажениям информации и установление взаимозависимостей между признаками с помощью возможностей алгоритмов дублирования информации.

Для решения поставленных задач необходимо:

· обучить сеть по сформированному задачнику;

· минимизировать количество признаков и оценить точность решения задачи классификации на полученном наборе (M`) в сравнении с решением по всему задачнику;

· найти дубли всех видов и сформировать на их основе наборы повышенной надежности;

· оценить качество решения задачи классификации в случае искажений информации;

· проанализировать полученные результаты.

Выполним последовательно все эксперименты и оценим возможность применения метода дублирования информации для данной выборки.

3.2. Минимальный набор признаков

На первом этапе экспериментов создаем нейронную сеть со структурой, предлагаемой программным продуктом (по умолчанию). Такая сеть является трехслойной и содержит по 10 нейронов на каждом слое и имеет характеристику 0,1. Обучаем сеть решать поставленную задачу классификации по предлагаемому задачнику, и тестируем полученные результаты (по каждому классу исхода болезни) по следующим параметрам:

· правильно расклассифицировано;

· неуверенно;

· неправильно.

Как видно (табл. 3.1) нейронная сеть обучилась правильно расклассифицировать все объекты, при этом неуверенного решения задачи, так же как и неправильного, нет (0%). Таким образом, для решения поставленной задачи достаточно трехслойной сети с предложенной структурой.

Осуществляя автоматическую минимизацию количества входных сигналов, нейросетевой имитатор оставил для решения задачи всего 50 признаков (табл. 3.2), которые в дальнейшем будем считать прототипами для следующей серии экспериментов с дублированием информации. При этом тестирование сети, способной классифицировать объекты по заданным классам показывает, что правильно было распределено 100% объектов и неуверенность в решении задачи отсутствует (результаты тестирования аналогичны результатам в табл. 3.1).

Таблица 3.1

Результаты тестирования

Класс	Тестируемый параметр
Класс	Правильно, %	Неуверенно, %	Неправильно, %	Всего
Класс 1	100	0	0	480
Класс 2	100	0	0	8
Класс 3	100	0	0	2
Класс 4	100	0	0	16
Класс 5	100	0	0	8
Класс 6	100	0	0	2
Класс 7	100	0	0	7
Класс 8	100	0	0	6

Таблица 3.2

Минимальный набор признаков


№	Порядковый номер признака в исходной выборке	Характеристика признака (см. прил. 1)	№	Порядковый номер признака в исходной выборке	Характеристика признака (см. прил. 1)
1.	3	SEX	26.	71	N_P_ECG_P_08
2.	12	ZSN_A	27.	73	N_P_ECG_P_10
3.	15	NR_02	28.	75	N_P_ECG_P_12
4.	21	NP_04	29.	76	FIBR_TER_01
5.	22	NP_05	30.	77	FIBR_TER_02
6.	24	NP_08	31.	83	GIPO_K
7.	28	ENDOCR_02	32.	85	GIPER_NA
8.	30	ZAB_LEG_01	33.	88	AST_BLOOD
9.	31	ZAB_LEG_02	34.	91	ROE
10.	33	ZAB_LEG_04	35.	96	R_AB_1_N
11.	34	ZAB_LEG_06	36.	98	R_AB_3_N
12.	39	O_L_POST	37.	102	NITR_S
13.	40	K_SH_POST	38.	103	NA_R_1_N
14.	41	MP_TP_POST	39.	105	NA_R_3_N
15.	43	GT_POST	40.	109	LID_S_N
16.	44	FIB_G_POST	41.	111	ANT_CA_S_N
17.	49	IM_PG_P	42.	112	GEPAR_S_N
18.	51	RITM_ECG_P_02	43.	114	TIKL_S_N
19.	52	RITM_ECG_P_04	44.	119	FIBR_JELUD
20.	57	N_R_ECG_P_02	45.	121	OTEK_LANC
21.	60	N_R_ECG_P_05	46.	122	RAZRIV
22.	61	N_R_ECG_P_06	47.	123	DRESSLER
23.	66	N_P_ECG_P_03	48.	124	ZSN
24.	69	N_P_ECG_P_06	49.	125	REC_IM
25.	70	N_P_ECG_P_07	50.	126	P_IM_STEN

3.3. Реализация алгоритмов дублирования

Следующим шагом исследований является апробация всех видов дублирования на поставленной задаче классификации.

Эксперименты будем проводить в следующем порядке:

· определим прямой дубль первого рода;

· сформируем косвенный дубль первого рода;

· найдем прямые дубли второго рода для каждого прототипа и составим полный прямой дубль второго рода;

· найдем полный косвенный дубль второго рода на базе косвенных дублей второго рода для каждого прототипа в отдельности.

Прямой дубль первого рода (ПДПР)

Выполняя последовательно алгоритм поиска данного вида дублей (см. рис. 2.2), получаем следующие результаты:

1. Нейронная сеть способна решать поставленную задачу по выборке, в составе которой отсутствует минимальный набор признаков, то есть на наборе M-M`. Этот результат говорит о том, что применение прямого дублирования имеет смысл.

2. Для данного набора прототипов существует набор дублеров, способный если не полностью, то частично заменить их отсутствие.

3. Этот набор состоит из 24 дублеров (см. прил. 3 табл. 1). При этом нейронная сеть правильно решает задачу классификации и на данном наборе дублеров со сто процентной точностью.

4. Имея после эти экспериментов набор прототипов и набор дублеров, можно сформировать набор повышенной надежности (см. прил. 3 табл. 1) на базе прямого дубля первого рода (S^1п_пн).

5. Получена структурная схема иерархической зависимости признаков (рис. 3.1).

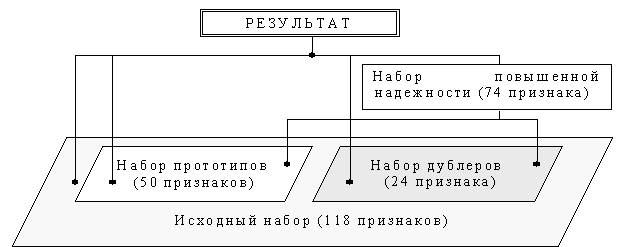
Рис. 3.1. Структурная схема иерархической зависимости признаков
на базе ПДПР

Косвенный дубль первого рода (КДПР)

Для определения косвенного дубля первого рода необходимо воспользоваться задачником, в состав которого входит весь набор признаков M и перевести признаки-прототипы в разряд результатов (см. рис. 2.3), обучить сеть решать задачу вычисления этих результатов на выборке с набором M-M` и еще раз провести минимизацию количества признаков.

Эксперименты показали, что нейронная сеть не может качественно решить поставленную задачу (прил. 3 табл. 2). Поэтому поиск косвенного дубля первого рода не имеет смысла – сеть, неспособная решить задачу на базе выборки с набором признаков большим, чем набор дублеров, тем более не сможет его определить. Задача минимизации признакового пространства M-M` является нецелесообразной. Таким образом получаем, что для набора прототипов не представляется возможным определить набор дублеров с помощью косвенного дубля первого рода для исследуемой базы данных и нейронной сети с установленными характеристиками.

Прямой дубль второго рода (ПДВР)

Теперь определим прямые дубли второго рода (см. рис. 2.5) для каждого из прототипов и составим полный прямой дубль второго рода. Алгоритм дублирования такого рода подробно описан в главе 3.

Результаты реализации этого алгоритма (см. прил. 3 табл. 3) показывают:

· для всех прототипов существуют прямые дубли второго рода;

· наибольшее количество дублеров (51 шт.) имеет прототип под номером 125 “Рецидив инфаркта миокарда (REC_IM)”;

· наименьшее количество дублеров (17 шт.) у прототипа, порядковый номер которого равен 60 “Пароксизмы фибрилляции предсердий на ЭКГ при поступлении (n_r_ecg_p_05)”;

· чаще всего (49 раз) дублером является признак под номером 122 “Разрыв сердца (RAZRIV)”;

· а реже всех (1 раз) участвуют в дублях признаки 11 “Длительность течения артериальной гипертензии (DLIT_AG)” и 92 “Время, прошедшее от начала ангинозного приступа до поступления в стационар (TIME_B_S)”;

· двадцать один признак вообще не принимает участия в дублях и не входит в состав прототипов;

· полный прямой дубль второго рода состоит из 97 дублеров, что составляет 82% от количества первоначального набора признаков;

· так как все прототипы выступают и в роли дублеров, то набор повышенной надежности будет соответствовать полному прямому дублю второго рода;

· для каждого из прототипов можно построить схему зависимости признаков (например, для признака под порядковым номером 60 и 96 в исходной выборке схема зависимостей изображена на рис. 3.2).

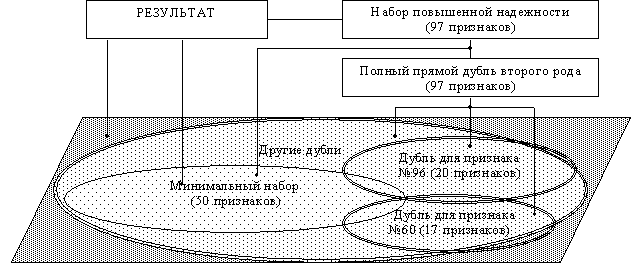Рис. 3.2. Иерархическая структура зависимости признаков на базе ПДВР

Косвенный дубль второго рода (КДВР)

Согласно процессу формирования набора повышенной надежности на базе косвенного дубля второго рода (см. рис. 2.6) выполняем эксперименты, в которых последовательно переводим каждый из прототипов в разряд результатов и находим минимальный набор признаков, способный вычислять его значение. При этом работа выполняется на выборке с набором признаков M-1 без участия исходного результата. Совокупность полученных пятидесяти дублей данного вида и будет являться полным косвенным дублем второго рода. Полученные результаты дублирования (см. прил. 3 табл. 4) выглядят следующим образом:

· нейронная сеть способна вычислять значения прототипов и определить минимальные наборы для этих вычислений;

· полный косвенный дубль второго рода включает в себя 100 дублеров;

· наибольшее количество дублеров (42 штук) имеет прототип номер 109 “Введение лидокаина в ОРиИТ (LID_S_N)”;

· наименьшее количество дублеров (2 штуки) у прототипа номер 76 “Проведение фибринолитической терапии целиазой 750 тыс. ЕД (fibr_ter_01)”;

· чаше всего в роли дублера (25 раз) выступает признак под номером 60 “Пароксизмы фибрилляции предсердий на ЭКГ при поступлении (n_r_ecg_p_05)”;

· а реже (1 раз) – признаки под номерами 84 “Содержание К⁺ в сыворотке крови (K_BLOOD)”, 86 “Содержание Na в сыворотке крови (Na_BLOOD)” и 90 “Содержание лейкоцитов в крови (´10⁹ /л) (L_BLOOD)”;

· все прототипы хотя бы один раз входят в состав дублей, поэтому набор повышенной надежности будет соответствовать полному косвенному дублю второго рода.

Анализируя полученные дубли можно определить набор признаков, которые не принимают участи в процессах дублирования информации (см. прил. 3 табл. 5). Их число составило 18 штук, так же как и для косвенного дубля второго рода, который содержит наибольшее количества признаков. Схема иерархической структуры пространства признаков приведена на рис. 3.3.

Рис. 3.3. Иерархическая структура признакового пространства на базе КДВР

Следующим этапом проводимых экспериментов является анализ устойчивости нейросетевых решений на различных наборах повышенной надежности к искажениям входной информации.

3.4. Оценка качества решения задачи классификации в случае искажения информации для различных наборов признаков

Сформируем наборы повышенной надежности на базе различных видов дублей с помощью объединения набора прототипов и соответствующего дубля. В итоге состав различных наборов повышенной надежности выглядит следующим образом:

· S^1п_пн	- состоит из 75 признаков;
· S^1к_пн	- отсутствует, так как нейронная сеть не может решить задачу одновременного вычисления всего набора прототипов;
· S^2п_пн	- включает в себя 97 признаков, количество которых совпадает с количеством полного прямого дубля второго рода;
· S^2к_пн	- в его состав вошло 100 признаков, что соответствует полному дублю.

Для проведения экспериментов с искаженной информацией, сформируем три выборки на базе исходного задачника. В первой выборке внесем искажения информации в наиболее информативный признак (номер 122) в 53 объекта (10% от общего количества). Во второй выборке – в произвольных местах в тринадцати прототипах и том же объеме примеров (686 искажений). В третьей – в 50% прототипах (1325 искажений).

Протестируем решение задачи нейрсетью по следующим направлениям: количество правильных ответов, количество неуверенных ответов и количество неправильных ответов для каждого набора в отдельности.

Результаты экспериментов показывают (табл. 3.3), что искажения информации не влияют на качество классификации по задачнику со всем набором признаков и с наборов повышенной надежности, основанном на косвенном дубле второго рода. Однако качество решений задачи на базе других наборов признаков ухудшается в зависимости от роста количества искажений.

Таблица 3.3

Результаты тестирования нейросети по выборкам с искаженной информацией

Вид набора	Характер оценки	Значение оценки в случае:
Вид набора	Характер оценки	отсутствия искажений	искажений в 122 признаке	искажений 10% прототипов	искажений 50% прототипов
М	Правильно	529 (100%)	529 (100%)	529 (100%)	529 (100%)
	Неуверенно	0 (0%)	0 (0%)	0 (0%)	0 (0%)
	Неправильно	0 (0%)	0 (0%)	0 (0%)	0 (0%)
М`	Правильно	529 (100%)	518 (97,92%)	523 (98,87%)	507 (95,84%)
	Неуверенно	0 (0%)	9 (1,7%)	0 (0%)	16 (3,03%)
	Неправильно	0 (0%)	2 (0,38%)	6 (1,13%)	6 (1,13%)
S^1п_пн	Правильно	529 (100%)	529 (100%)	527 (99,62%)	524 (99,06%)
	Неуверенно	0 (0%)	0 (0%)	1 (0,19%)	3 (0,56%)
	Неправильно	0 (0%)	0 (0%)	1 (0,19%)	2 (0,38%)
S^2п_пн	Правильно	529 (100%)	528 (99,81%)	529 (100%)	528 (99,81%)
	Неуверенно	0 (0%)	1 (0,19%)	0 (0%)	0 (0%)
	Неправильно	0 (0%)	0 (0%)	0 (0%)	1 (0,19%)
S^2к_пн	Правильно	529 (100%)	529 (100%)	529 (100%)	529 (100%)
	Неуверенно	0 (0%)	0 (0%)	0 (0%)	0 (0%)
	Неправильно	0 (0%)	0 (0%)	0 (0%)	0 (0%)

Более того, из таблицы видно, что, по сравнению с качеством решения задачи сетью по минимальному набору признаков, наборы повышенной надежности на базе каждого из дублей по праву носят свое название, так как результаты работы нейронной сети в условиях искажения информации в базе данных лучше, чем в случае с набором прототипов. А наиболее зависимым от точности данных оказалось решение нейронной сети, основанное на минимальном наборе признаков (на прототипах) не содержащем дублеров информации.

Таким образом можно сказать, что для решения поставленных задач наиболее оптимальным набором признаков, позволяющих максимально удовлетворить все условия задачи, является выборка, включающая в себя набор повышенной надежности на базе косвенного дубля второго рода. Использование этого дубля удовлетворяет условию устойчивости решения к искажениям во входных данных и сокращению числа входных признаков (на 15%).

Выводы к главе 3

1. Применение дублирования при решении задач классификации показало, что выборки, с большим количеством признаков, содержат не только минимальный набор признаков, но некоторые виды дублирующих наборов. А на основе выявленных видов дублирующих наборов четко выстраивается структурная зависимость в пространстве признаков.

2. Эксперименты показали, что менее устойчивыми к искажениям информации являются нейросетевые системы, работающие на выборке с минимальным набором признаков. Системы же, решение задачи в которых основано на наборах повышенной надежности, в меньшей степени зависят от искажений во входных данных.

3. Анализ состава наборов признаков (минимального, дублирующих и повышенной надежности) показал, что ряд из них не входит ни в минимальный набор, ни в набор дублеров, следовательно, они не содержат информации, необходимой для решения задачи. При этом анализ изменения ошибки классификации доказал, что эти признаки являться зашумляющими, то есть качество решение задачи снижается, если они присутствуют в выборке.

ГЛАВА 4. ДУБЛИРОВАНИЕ ИНФОРМАЦИИ НА ПРИМЕРЕ РЕШЕНИЯ ЗАДАЧИ ПРОГНОЗИРОВАНИЯ РЕЗУЛЬТАТИВНОСТИ ТРУДА ПРЕПОДАВАТЕЛЯ

4.1. Характеристика информации и постановка задачи

Для проведения исследований в этом направлении воспользуемся информацией, предоставленной сотрудниками отдела кадров Красноярского государственного торгово-экономического института.

Данная информация оформлена в виде таблицы, которая состоит из 51 примера и 73 признаков. Каждый исходный признак в предложенной базе данных имеет свою определенную числовую кодировку, как правило, это 1 или 0 (“Да” или “Нет”). Эти признаки, характеризующие претендента на должность, делятся на три группы (см.прил. 4):

· первая группа характеризует деловые и профессиональные качества (стаж работы, количество публикаций, частоту сменяемости рабочих мест и т.д.),

· вторая и третья группы (это графоаналитическая экспертиза и анализ внешнего вида по фотографии) определяют характер и психологические особенности претендента.

Учитывая специфику работы преподавателя, результатом для оценки его деятельности в данном случае является средний балл анкеты “Преподаватель глазами студентов” (см. прил. 5). Результат имеет формат числа, которое лежит в интервале от 0 до 5 (например, 3, 4,7 или 3,5). Эти данные призваны помогать руководителю организации в принятии решений об отборе персонала на вакантную должность, то есть прогнозировать отношения преподаватель-студент на начальном этапе управления персоналом. Решение такой задачи связано с проблемой определения результатов труда претендента и выявления его психологических особенностей для работы в условиях конкретной организации [10].

Однако это решение затруднено относительно большим количеством признаков для визуального анализа информации. А статистической обработке предложенная таблица данных не поддается, так как нарушено основное правило, предъявляемое к выборке: количество примеров должно быть намного больше, чем количество признаков. И, хотелось бы отметить, что большинство современных организаций на сегодняшний день имеют достаточно большое количество невостребованной информации такого рода.

Поэтому, прежде всего, возникла задача выбора метода обработки информации, способного вычислять результат с точностью ±0,3 балла, минимизация исходного набора признаков, а затем задача обработки данной таблицы с помощью дублирования информации для получения дополнительных сведений и повышения надежности системы от неумышленных искажений информации.

Учитывая все требования, предъявляемые к информации управленческого характера, информационное и техническое обеспечение современных организаций, воспользуемся нейросетевыми технологиями как инструментом для ее анализа и обработки. Все эксперименты основаны на возможностях нейросетевого имитатора NeuroPro и проводятся по следующей схеме:

1. Обучение нейронной сети, способной наиболее точно вычислять результат.

2. Снижение размерности исследуемого признакового пространства с целью отбора наиболее информативных показателей, визуализация данных и сжатие массивов обрабатываемой и хранимой информации.

3. Реализация алгоритмов дублирования как способа “защиты” выборки от неумышленных искажений информации.

4.2. Обучение сети и минимизация количества признаков

Для начала обучим нейронную сеть по базе данных, сформированной на основе выборки, оценим ошибку вычислений и минимизируем количество признаков. Результаты тестирования (табл. 4.1) созданной трехслойной сети с характеристикой 0,1 и количеством нейронов равному 10 в каждом слое (структура предложена программой) показывают, что выбранная нейронная сеть вычисляет результат по всем предложенным примерам выборки, при этом значение средней ошибки вычислений равно 0,0988127, а значение максимально ошибки – 0,189229. Это говорит о том, что данная сеть вычисляет результат на 40% точнее, чем требовалось в задаче. Следовательно, нейросеть способна обрабатывать предложенную таблицу данных, более того, она способна предсказывать результат с меньшим отклонением от реального значения. Этот эксперимент открывает еще одну область применения нейросетевых технологий – оценка результатов деятельности персонала в социально-экономических системах.

Таблица 4.1

Результаты тестирования нейронной сети по всему набору признаков


№ примера	Ответ	Прогноз сети	Ошибка	№ примера	Ответ	Прогноз сети	Ошибка
1	4,7	4,564834	0,1351664	27	3,8	3,933739	-0,1337394
2	4,6	4,511941	0,08805857	28	4,6	4,567887	0,0321127
3	4,5	4,586222	-0,08622169	29	3,3	3,488559	-0,1885585
4	4,4	4,212804	0,1871957	30	4,3	4,281864	0,01813631
5	3,7	3,531701	0,1682987	31	4,5	4,6522	-0,1522002
6	4,2	4,250319	-0,050319	32	3,8	3,769537	0,03046327
7	4,6	4,505969	0,09403095	33	4,7	4,572262	0,1277377
8	3,6	3,635629	-0,03562894	34	4,5	4,602953	-0,1029534
9	3,5	3,619191	-0,1191907	35	4,3	4,362319	-0,06231947
10	4,6	4,517105	0,0828949	36	4	3,865637	0,1343634
11	3	3,088985	-0,08898497	37	3,7	3,668845	0,03115458
12	4,7	4,634391	0,06560917	38	3,7	3,752254	-0,05225425
13	4	4,129437	-0,129437	39	4,1	4,241192	-0,1411923
14	4	4,147848	-0,1478481	40	4,3	4,205741	0,09425907
15	4,5	4,349964	0,1500363	41	3,7	3,510771	0,189229
16	4,6	4,679758	-0,07975759	42	4,3	4,392426	-0,09242649
17	4	3,951845	0,04815459	43	4,3	4,321236	-0,02123613
18	4,2	4,15826	0,04173965	44	3,4	3,49298	-0,09298048
19	2,8	2,816724	-0,01672406	45	4	4,170143	-0,1701431
20	3,4	3,3422	0,0578002	46	4,8	4,667688	0,1323116
21	4,1	4,250048	-0,1500482	47	4,7	4,582488	0,1175124
22	4,3	4,142254	0,1577461	48	4	4,18909	-0,1890898
23	4,3	4,263924	0,03607588	49	4,7	4,617945	0,08205529
24	3,4	3,390842	0,00915756	50	4,1	4,180614	-0,08061447
25	4,9	4,722338	0,1776623	51	4,2	4,192139	0,00786133
26	3,6	3,441244	0,1587563

Всего: 51; Правильно: 51 (100%);				Неправильно: 0 (0%);
Средняя ошибка: 0,0988127;				Максимальная ошибка: 0,189229.

Так как программа NeuroPro позволяет автоматически сокращать число входных сигналов и формировать минимальные наборы признаков, то, используя данную возможность, создадим такой набор и еще раз исследуем точность вычисления результирующей характеристики.

После автоматического сокращения числа входных сигналов из 73 признаков программа оставила всего 11 при достаточно хорошем результате вычислений. В табл. 4.2 приведен перечень признаков (прототипов), вошедших в минимальный набор и распределенных в порядке их значимости.

Таблица 4.2

Минимальный набор признаков

Порядковый номер признака	Характеристика признака	Значимость признака
18	Последняя работа педагогическая	1
30	Буквы крупные	0,876149
35	Прямое написание	0,803882
29	Буквы средние	0,788738
45	Длинные петли нижней части букв	0,748162
57	Лицо круглое	0,737079
54	Плавный поток ровных букв	0,736483
50	Экстравагантные заглавные буквы	0,681887
22	Обучение в аспирантуре/докторантуре	0,669261
51	Разные по размеру буквы	0,606694
10	Проживает рядом с работой	0,505956

Результаты тестирования сети после сокращения количества входных сигналов (табл. 4.3) показывают, что сеть успешно предсказывает результат по всем примерам, но качество вычислений ухудшается (по сравнению с вычислениями на базе исходного набора признаков) на 10% (табл. 4.4). Однако максимальное значение ошибки не выходит за пределы допустимых отклонений, более того, результат предсказывается с точность на 30% лучше заданной (±0,3 балла), поэтому при необходимости можно воспользоваться лишь минимальным набором признаков для оценки результативности деятельности преподавателей.

Таблица 4.3

Результаты тестирования нейронной сети по минимальному набору признаков


№ примера	Ответ	Прогноз сети	Ошибка	№ примера	Ответ	Прогноз сети	Ошибка
1	4,7	4,501318	0,1986815	27	3,8	3,97676	-0,1767599
2	4,6	4,407734	0,1922656	28	4,6	4,51272	0,08728037
3	4,5	4,351751	0,1482491	29	3,3	3,401172	-0,1011724
4	4,4	4,596153	-0,1961533	30	4,3	4,165644	0,1343558
5	3,7	3,548701	0,1512994	31	4,5	4,475142	0,02485752
6	4,2	4,122122	0,07787819	32	3,8	3,980754	-0,1807539
7	4,6	4,486978	0,1130219	33	4,7	4,50788	0,1921198
8	3,6	3,751646	-0,1516463	34	4,5	4,346823	0,1531768
9	3,5	3,592304	-0,09230375	35	4,3	4,459353	-0,159353
10	4,6	4,426985	0,1730152	36	4	3,887701	0,112299
11	3	3,184931	-0,184931	37	3,7	3,887701	-0,187701
12	4,7	4,596153	0,1038467	38	3,7	3,711635	-0,01163511
13	4	3,956284	0,04371643	39	4,1	4,227572	-0,1275724
14	4	4,143391	-0,1433911	40	4,3	4,175501	0,1244987
15	4,5	4,703939	-0,203939	41	3,7	3,669543	0,03045673
16	4,6	4,479212	0,1207877	42	4,3	4,407734	-0,1077344
17	4	3,920425	0,0795753	43	4,3	4,124745	0,1752546
18	4,2	4,031225	0,1687753	44	3,4	3,37266	0,02734032
19	2,8	2,861704	-0,06170363	45	4	4,172176	-0,1721764
20	3,4	3,426845	-0,02684507	46	4,8	4,613778	0,1862219
21	4,1	4,271272	-0,1712722	47	4,7	4,684228	0,01577206
22	4,3	4,248971	0,05102854	48	4	4,195423	-0,1954231
23	4,3	4,271272	0,02872782	49	4,7	4,536718	0,1632816
24	3,4	3,224185	0,1758145	50	4,1	4,179564	-0,07956447
25	4,9	4,69099	0,2090096	51	4,2	4,10666	0,09334011
26	3,6	3,426845	0,1731549


Всего: 51; Правильно: 51 (100%);				Неправильно: 0 (0%);
Средняя ошибка: 0,1266889;				Максимальная ошибка: 0,290096.

Таблица 4.4

Сравнение ошибок вычислений до и после минимизации

Вид ошибки	Значение
Вид ошибки	до минимизации	после минимизации
Средняя ошибка	0,0988127	0,1266889
Максимальная ошибка	0,189229	0,2090096

Ухудшение качества вычислений говорит о том, что сеть, пренебрегая частью признаков, теряет некоторое количество полезной информации. И эти потери окажут существенное влияние в процессе работы с выборкой в случае возникновения искажений в ряде входных данных. Данное замечание весьма важно, так как деятельность кадровых служб не исключает внесения сотрудником неумышленных ошибок во время внесения дополнительных примеров, анализа и обработки данной таблицы.

Поэтому предлагается проанализировать взаимозависимость данных с помощью различных алгоритмов дублирования и определить наиболее оптимальный вариант окончательного набора признаков, способный удовлетворить основные требования по сокращению выборки и точности вычислений.

4.3. Прямой дубль первого рода (ПДПР)

Согласно алгоритму формирования прямого дубля первого рода (см. рис. 2.2) определим набор дублеров и набор повышенной надежности для полученных выше прототипов.

Из первоначального набора признаков выключаем (выбрасываем) все признаки, принадлежащие минимальному набору. Обучаем сеть решать задачу на выборке с оставшимися признаками и, минимизируя их количество, находим дублеров исключенной информации.

В результате реализации данного алгоритма получаем дубль (см. прил. 6 табл. 1), в состав которого входит 19 признаков: 4, 6, 12, 14, 19, 20, 25, 28, 34, 41, 44, 49, 55, 56, 58, 59, 65, 68, 70 (характеристику признаков см. в прил. 4). При этом максимальная ошибка вычислений равна 0,207231 и средняя ошибка – 0,130369. По сравнению с первоначальным набором признаков качество вычисления результата ухудшилось на 10%, а по сравнению же с результатами экспериментов по минимальному набору оно улучшилось на 0,5%. Такое значение ошибок не выходит за пределы требуемой в задаче точности вычислений, поэтому, даже используя только этот набор дублеров, сеть способна решать поставленную задачу. Таким образом, полученный минимальный набор признаков, состоящий из 19 штук, является прямым дублем первого рода и показывает, какие признаки стоит оставить для дальнейшей работы с выборкой, а какими можно пренебречь.

Формируя окончательный набор признаков, полученный с помощью комбинирования набора прототипов и дублеров, получаем набор повышенной надежности, в состав которого вошло 30 признаков. Решение задачи, основанное на данном наборе, показывает, что нейронная сеть предсказывает результат на 5% лучше, чем по набору прототипов, на 4% - по сравнению с набором дублеров и на 6% хуже по сравнению с результатом максимальной ошибки вычислений по всему набору.

Проверим, действительно ли данный набор признаков можно назвать набором повышенной надежности. Для этого выбираем несколько признаков из минимального набора, наиболее подверженных неумышленным искажениям, и по некоторому числу примеров заносим в эти признаки неверную информацию. После этого решаем задачу прогнозирования результата на искаженном задачнике и сравниваем точность вычислений результата, основанных на исходном задачнике и искаженном.

Проверка надежности

Внесем последовательно искажения информации в наиболее значимый признак (18) из минимального набора, в половину признаков минимального набора и во всю совокупность признаков минимального набора. Определим среднюю ошибку вычислений для каждой позиции в сетях с минимальным набором признаков и с набором повышенной надежности. Сравним среднее отклонение ошибок вычислений по минимальному набору и по набору повышенной надежности (табл. 4.5).

Из таблицы видно, что более точными вычислениями даже после искажения информации являются те, которые принадлежат выборке с набором признаков повышенной надежности. Вследствие этого, набор такого рода действительно называется набором повышенной степени надежности и оправдывает свое назначение.

Таблица 4.5

Результаты вычислений на основе выборок с искаженной информацией

	Значение ср. ошибки				Изменение ср. ошибки %
Набор	Исходное	Искажение в 18 признаке	Искажение в 10% прототипов (92 искажения)	Искажения в 50% прототипов (459 искажений)	Изменение ср. ошибки %
Минимальный	0,1266889	0,131359	0,1291419	0,1483551	»+7,6%
Повышенной надежности на базе ПДПР	0,108108	0,1094385	0,109233	0,110633	»+1,5%

4.4. Косвенный дубль первого рода (КДПР)

Решение задача косвенного дубля первого рода состоит в том, чтобы по набору оставшихся признаков (за минусом признаков минимального набора) восстановить значения признаков начального минимального множества прототипов (см. рис. 2.3).

Для решения данной задачи необходимо перевести все признаки, принадлежащие изначально минимальному набору, в разряд “результаты”. (При этом исходный результат прогнозирования не используется.) Далее необходимо обучить сеть и провести минимизацию входных сигналов (признаков). Этот набор и будет являться косвенным дублем первого рода.

После пошагового выполнения данного процесса решения задачи получаем дубль (см. прил. 6 табл. 2), состоящий из 16 признаков: 4, 5, 13, 15, 21, 33, 34, 41, 47, 48, 49, 52, 53, 56, 59, 63 (характеристику признаков см. в прил. 4).

Так как все 16 признаков входят в набор косвенного дубля первого рода, то окончательный набор повышенной надежности для решения задачи прогнозирования исходного результата будет состоять из минимального набора плюс косвенный дубль первого рода. В эту совокупность входит 27 признаков. При этом максимальная ошибка составляет 0,204431, а средняя ошибка вычислений равна 0,095828.

Качество вычисления результата имеет следующее соотношение: оно хуже на 8% по сравнению с решением задачи по всему набору признаков и лучше на 2% по сравнению с вычислениями по набору прототипов.

Проверка надежности

Для того чтобы определить зависимость средней ошибки вычислений в исходном минимальном и в окончательном наборе признаков воспользуемся одной и той же базой данных с искаженной информацией и определим значение средней ошибки (табл. 4.6).

Таблица 4.6

Результаты вычислений на основе выборок с искаженной информацией

	Значение ср. ошибки
Набор	Исходное	Искажение в 18 признаке	Искажение в 10% прототипов (92 искажения)	Искажения в 50% прототипов (459 искажений)	Изменение ср. ошибки, %
Минимальный	0,1266889	0,131359	0,1291419	0,1483551	»+7,6%
Повышенной надежности на базе КДПР	0,095828	0,1011221	0,1019633	0,1021166	»+6,2%

Результаты экспериментов, отраженные в данной таблице, показывают, что более точными вычислениями даже после искажения информации являются те, которые принадлежат выборке с набором признаков повышенной надежности. Хотя искажения в случае применения косвенного дубля первого рода и влияют на качество вычислений результата больше, чем при использовании в окончательном наборе признаков прямого дубля первого рода, тем не менее, устойчивость к условиям искажений данных системы достигается.

4.5. Прямой дубль второго рода (ПДВР)

По своей сути алгоритм определения прямого дубля второго рода аналогичен определению прямого дубля первого рода. Единственным отличием является то, что при определении прямого дубля второго рода исключается не вся совокупность признаков минимального набора, а лишь тот признак (или та часть признаков), дубль для которого необходимо найти (см. рис. 2.5).

В данном случае, исходя из условия поставленной задачи, требуется найти 11 прямых дублей второго рода. Вследствие этого и окончательный набор признаков будет состоять из минимального набора (11 признаков) плюс дубли для всех признаков минимального множества.

В следующей серии экспериментов найдем прямые дубли второго рода для каждого из прототипов, определим полный прямой дубль второго рода и сформируем окончательный набор признаков повышенной надежности.

В состав множества повышенной надежности вошло 55 признаков (см. прил. 6 табл. 3) и видно, что для данной выборки полный прямой дубль второго рода является и множеством повышенной надежности. Вероятно, что аналогичный результат будет получен для большинства выборок. И очевидно, что полный прямой дубль второго рода может содержать в себе количество признаков меньшее, чем множество повышенной надежности, и что множество повышенной надежности будет больше тогда, когда полный прямой дубль второго рода не содержит хотя бы один из признаков минимального набора.

Из таблицы видно:

· 20 признаков не вошли в состав набора повышенной надежности (8, 9, 36, 37, 38, 39, 40, 47, 58, 60, 61, 64, 66, 67, 69, 70, 73, 75),

· наибольшее количество дублеров имеет прототип под номером 45 “Длинные петли нижней части букв” – 22 дублера,

· наименьшее количество дублеров (10 штук) у прототипа под номером 50 “Экстравагантные заглавные буквы”,

· за исключением признака под номером 35 “Прямое написание”, все прототипы в некоторых случаях являются так же и дублерами,

· наиболее часто встречающимся среди дублеров является признак под номером 28 “Буквы маленькие”, его появление зафиксировано в девяти дублях из одиннадцати.

Данная информация несет дополнительные сведения о наборе признаков и их взаимосвязях. Например, на базе набора прототипов можно сформировать выборку с первичной информацией в данных, а на базе набора дублеров – выборку из вторичной информации. Таким образом, получаем своего рода “информационный фильтр”, который позволяет ранжировать данные в порядке их значимости для принятия решений. Что в свою очередь позволит руководителю организации сократить время на процесс отбора кадров в целом.

Проверка надежности

Определим зависимость средней ошибки вычислений в исходном минимальном и в множестве повышенной надежности с помощью баз данных с искаженной информацией. То есть на этих базах последовательно обучим сеть с минимальным набором признаков и сеть, построенную на основе множества повышенной надежности S^2п_пн. В первой базе данных заложены искажения информации в 18 признаке по некоторым примерам, во второй – в 10% признаках, в третьей – в произвольно выбранном месте в 50% выборки. Определим изменения среднего значения ошибки вычислений и сравним, как же искажения информации влияют на качество вычислений в случае с минимальным множеством признаков и множеством повышенной надежности S^2п_пн (табл. 4.7).

Таблица 4.7

Результаты вычислений на основе выборок с искаженной информацией

	Значение ср. ошибки
Набор	Исходное	Искажение в 18 признаке	Искажение в 10% прототипов (92 искажения)	Искажения в 50% прототипов (459 искажений)	Изменение ср. ошибки, %
Минимальный	0,1266889	0,131359	0,1291419	0,1483551	»+7,6%
Повышенной надежности на базе ПДВР	0,0999919	0,1011991	0,1012838	0,1021598	»+1,5%

Что касается оценки качества вычислений, то тестирование нейронной сети показало: изменение значения средней ошибки вычислений по набору повышенной надежности, основанном на прямом дубле второго рода, в случае искажения информации меньше, чем на базе набора прототипов.

Как и для рассмотренных дублей, результаты экспериментов показывают, что более надежными являются множества, в состав которых входит объединение минимального набора признаков и дубли. Так как вычисление результата на их основе происходит более точно.

4.6. Косвенный дубль второго рода (КДВР)

Для определения косвенного дубля второго рода для каждого признака проведем серию экспериментов по схеме, изображенной в главе 2 на рисунке 2.6. То есть для каждого признака из минимального множества выполним серию действий:

1. Переведем признак в разряд “результатов” и постараемся предсказать его значение с помощью вновь обученной нейронной сеть.

2. Найдем минимальный набор признаков для выборки такого рода, который и будет являться косвенным дублем второго рода для этого признака-результата.

3. Повторив последовательно действия 1 и 2 M` раз найдем дубли для всех признаков из минимального множества.

4. С помощью объединения всех дублей получим полный косвенный дубль второго рода и на его основе множество повышенной надежности S^2к_пн.

Результаты экспериментов по формированию косвенного дубля второго рода для каждого признака минимального множества показывают, что для данной выборки такие дубли существуют (см. прил. 6 табл. 4). При этом самое большое количество дублеров имеет дубль для 18-го признака “Последняя работа педагогическая” (17 дублеров), а самое маленькое – КДВР для 35-го признака “Прямое написание” (6 дублеров). Анализируя эти результаты можно сказать, что количество дублеров в дубле зависит от того, какую информацию они в себе содержат. То есть, можно сказать, что для 35-го признака существует всего шесть дублеров, способных частично заменить его отсутствие и “подстраховать” вычисление результата в основной выборке в случае неумышленного искажения информации во входных данных.

Несмотря на такие отличия в количестве, полный косвенный дубль второго рода содержит в себе 59 признаков, что составляет 81% от общего количества признаков. А окончательный же набор еще больше, так как в его состав, кроме дублеров, входит и минимальный набор. Вследствие этого он состоит из 61 признака, а это 85% от общего числа признаков. При этом 12 признаков (9, 26, 36, 37, 38, 39, 40, 64, 66, 69, 72, 73) не участвуют в процессе дублирования. Возможно они являются шумовыми.

Наибольшее количество раз дублем является признак под номером 14 “Наличие курсов повышения квалификации”, он встречается в этой роли шесть раз. А вот прототипы под номером 45 “Длинные петли нижней части букв” и номером 50 “Экстравагантные заглавные буквы” в роли дублеров не выступают ни разу.

Данный вид дублирования позволяет создать систему данных, способных вычислять значения прототипов и восстанавливать информационные пробелы. Более того, это свойство помогает вырабатывать рекомендации для усовершенствования отношений преподаватель-студент. Например, зная информативность дублеров можно, варьируя данными, определить изменение значения прототипов и, как следствие, изменение результата. Это в свою очередь позволяет давать общие рекомендации о качествах претендента, требующих коррекции и адаптации к условиям конкретной организации.

В заключение этих экспериментов с косвенными дублями второго рода остается решить только один вопрос: на самом ли деле окончательный набор признаков будет обладать повышенной надежность?

Проверка надежности

Как и в случае с прямым дублем второго рода определим зависимость средней ошибки вычислений от искажений информации для минимального множества M` и для полученного окончательного набора (табл. 4.8).

Таблица 4.8

Результаты вычислений на основе выборок с искаженной информацией

	Значение ср. ошибки
Набор	Исходное	Искажение в 18 признаке	Искажение в 10% прототипов (92 искажения)	Искажения в 50% прототипов (459 искажений)	Изменение ср. ошибки, %
Минимальный	0,1266889	0,131359	0,1291419	0,1483551	»+7,6%
Повышенной надежности на базе КДВР	0,1142652	0,1155792	0,1178998	0,1199973	»+3,1%

Из таблицы видно, что сеть, созданная на основе окончательного множества признаков, решает задачу более точно и более качественно, чем нейросеть использующая минимальный набор признаков. Она менее зависима от искажений информации в признаках прототипах, чем сеть, основанная на минимальном множестве и предыдущих видах дублей. Поэтому можно сказать, что полученный окончательный набор признаков действительно может называться набором повышенной надежности S^2к_пн.

4.7. Итоговые результаты анализа

Анализируя составы всех наборов повышенной надежности (см. прил. 6 табл. 5), сформированных на основе дублей различных видов, можно увидеть, что ни в один из них не вошли следующие признаки:

· №9 – Возраст младшего ребенка,

· №36 – Форма букв (-1 – угловатые, 0 – бесформенные, 1 – округлые),

· №37 – Строчки “ползут” (-1 – вниз, 0 – прямые, 1 – вверх),

· №38 – Размашистость почерка (-1 – сильная, 0 – средняя, 1 – легкая),

· №39 – Сила нажима (-1 – сильная, 0 – средняя, 1 – легкая),

· №40 – Стиль написания (-1 – раздельно, 0 – смешанный, 1 – слитно),

· №64 – Размер глаз (-1 - большие, 0 - средние, 1 - маленькие),

· №66 – Лоб (-1 - низкий, 0 - средний, 1 - высокий),

· №69 – Губы (-1 - тонкие, 0 - средние, 1 - пухлые),

· №73 – Телосложение (-1 - худощавое, 0 - среднее, 1 - крупное).

Можно предположить, что они являются “шумами” и отрицательно воздействуют на процесс решения задачи.

Проверим данное предположение с помощью сравнения ошибок вычислений сети, обученной решать задачу на выборке, в состав которой не входят данный ряд признаков и сети, решающей задачу по всему набору признаков (назовем такой набор сокращенным набором). Результаты тестирования (табл. 4.9) этого эксперимента действительно доказывают высказанное предположение. Результат вычислений по сокращенному набору признаков улучшился по сравнению с результатом по исходному набору признаков: минимальное значение ошибки вычислений сократилось на 16%, а значение максимальной ошибки – на 28%.

Таблица 4.9

Сравнение результатов обучения нейронных сетей с разным набором признаков

Вид ошибки	Значение ошибки обучения нейросети
	по всему набору признаков	по сокращенному набору признаков
Средняя ошибка	0,0988127	0,08263195
Максимальная ошибка	0,189229	0,13610845

А качество вычислений в случае искажений информации во входных данных при тех же условиях проверки, что и для всех наборов повышенной надежности, еще выше (табл. 4.10).

Таблица 4.10

Результаты вычислений на основе выборок с искаженной информацией

	Значение ср. ошибки
Набор	Исходное	Искажение в 18 признаке	Искажение в 10% прототипов (92 искажения)	Искажения в 50% прототипов (459 искажений)	Изменение ср. ошибки, %
Минимальный	0,1266889	0,131359	0,1291419	0,1483551	»+7,6%
Сокращенный	0,08263195	0,0829849	0,0831748	0,0833973	»+1%

Таким образом получаем, что эти десять признаков несут в себе информацию, отрицательно влияющую на качество работы нейронной сети и качество решения ею поставленной задачи.

На следующем этапе работы необходимо выяснить, какой из наборов повышенной надежности удовлетворит требованиям изначально поставленной задачи.

Исходя из условия задачи, можно выделить три основных критерия для выбора набора признаков:

· вычисление результата с точностью ±0,3;

· уменьшение размерности вектора входных сигналов;

· формирование такого окончательного набора признаков, который способен повысить устойчивость вычисление основного результата к неумышленным искажениям информации.

Обратим внимание на наборы повышенной надежности, сформированные на основе различных дублей (S^1п_пн, S^1к_пн, S^2п_пн, S^2к_пн). Условиям первого критерия удовлетворяют все наборы, а вот по отношению к остальным критериям наборы расположились следующим образом:

1. S^1п_пн- 30 признаков в наборе, изменение ошибки »+1,5%;

2. S^1к_пн- 27 признаков в наборе, изменение ошибки »+6,2%;

3. S^2п_пн- 55 признаков в наборе, изменение ошибки »+1,5%;

4. S^2к_пн- 62 признака в наборе, изменение ошибки »+3,1%.

Учитывая то, что минимальный набор составляет 11 признаков и изменение ошибки в случае искажения информации »+7,6%, то остановим свой выбор на наборе повышенной надежности, сформированном на основе прямого дубля первого рода. Таким образом, получаем окончательное решение - выборку, состоящую из 30 признаков, где результат вычисляется в среднем с точностью ±0,108108 в условиях искажений информации, а иерархическая структура зависимости признаков построена на базе трех уровней (рис. 4.1).

Если задаться целью – еще сократить количество признаков и при этом создать набор повышенной надежности, то можно экспериментальным путем определить признаки наиболее подверженные искажениям информации и построить для них дубли второго рода.

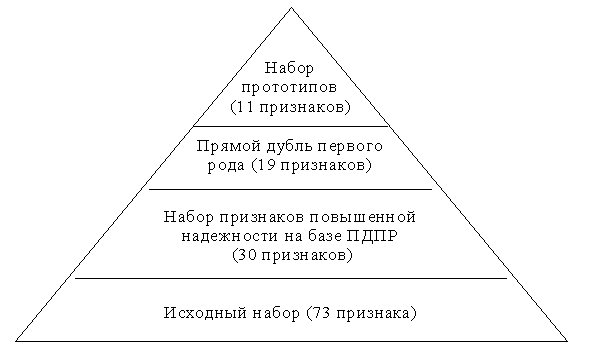
Рис. 4.1. Иерархическая структура признакового пространства

Таким образом, дублирование информации создает не только барьер искажениям информации во входных данных, но и является неплохим средствам анализа структуры пространства признаков с использованием нейросетевых подходов. С его помощью можно получать дополнительные знания о решаемой задаче, структуре данных и вырабатывать рекомендации для конкретной реализации управленческих решений.

Решая задачи дублирования информации, была рассмотрена еще одна область применение нейросетевых подходов к обработке информации – область управленческой деятельности современных организаций – оценка результатов деятельности преподавателя. Эта возможность имеет принципиальное значение, так как в современных условиях существования большинство организаций, обладая большим количеством информации, не способны ее использовать по назначению. В основном это связано с “отсутствием статистики” на современных российских предприятиях и с невозможностью обработки информации традиционными методами по причине ее несоответствия предъявляемым требованиям.

Выводы к главе 4

1. Результаты обработки информации из отдела кадров Красноярского государственного торгово-экономического института открывают еще одну область применения нейросетевых технологий – оценка результатов деятельности персонала в социально-экономических системах.

2. Применение дублирования при решении задачи прогнозирования результативности деятельности преподавателя со студентами показывает, что данная выборка содержат не только минимальный набор признаков, но и дублирующие наборы: прямой дубль первого рода, косвенный дубль первого рода, прямой дубль второго рода и косвенный дубль второго рода.

3. Эксперименты показали, что в случае возникновения искажений информации во входных данных нейросетевые решения на базе наборов повышенной надежности более устойчивы, чем результаты вычислений с использованием только минимального набора признаков.

4. Анализ состава наборов признаков показал, что ряд из них не входит ни в минимальный набор, ни в набор дублеров, более того они не содержат информации, необходимой для решения задачи. А анализ изменения ошибок вычисления доказал, что эти признаки являться зашумляющими, то есть качество решение задачи существенно ниже, если они присутствуют в выборке.

ЗАКЛЮЧЕНИЕ

Процесс формирования информации требует хорошего набора статистических данных, аналитических методов и современных информационных технологий. Предлагаемые различными науками традиционные методы обработки данных имеют свои определенные достоинства и недостатки. Каждый из таких методов хорош по-своему в определенной ситуации. Но наиболее соответствующие требованиям современного исследователя являются нейросетевые методы, созданные в процессе развития теории “искусственного интеллекта”.

Решая задачи минимизации количества входных сигналов в условиях возможного появления искажений информации во входных данных даже с помощью наиболее подходящих методов, исследователь сталкивается с риском понижения качества решения и полезности их алгоритмов. В этом случае уменьшать погрешность вычислений можно и целесообразно за счет увеличения пространства признаков путем добавления дублирующей информации из набора исходных данных.

Алгоритмы поиска дублеров основаны на минимизации пространства признаков, а процессы формирования на их основе наборов повышенной надежности к искажениям такого рода достаточно просты и имеют самостоятельное значение, не зависимо от методов минимизации пространства признаков. Кроме этого практическое применение данных алгоритмов показывает, что они могут войти в серию методов устанавливающих зависимости между признаками, объясняющих структуру пространства признаков и выявляющих иерархическую зависимость между характеристиками объектов исследования.

Реализованные алгоритмы дублирования способны выступать в роли помощников в принятии решений. Они позволяют вырабатывать информацию нового содержания и создавать базу для дальнейшего анализа и обработки. С их помощью можно расставлять приоритеты среди признаков, формировать отдельно выборки, состоящие из первичной и вторичной информации, фильтровать данные и т.п.

Совокупное участие всех признаков, входящих в дубли и набор прототипов показывает, что ряд признаков не входит ни в минимальный набор, ни в набор дублеров. Следовательно, такого рода признаки не содержат информации, необходимой для решения задачи. Более того, их присутствие в выборке порой оказывает отрицательное влияние на качество решения задачи. Таким образом, реализация алгоритмов дублирования позволяет делать предположение о характере признаков, о необходимости их участи и о наличии в них “шумовых” качеств.

Реализованные алгоритмы дублирования в процессе отбора кандидатов на вакантную должность преподавателя в Красноярском государственном торгово-экономическом институте показали, что с их помощью из имеющихся данных можно отобрать те, которые непосредственно требуются для решения задачи прогнозирования отношений преподаватель-студент в условиях возникновения искажений информации. Кроме этого, информация, полученная после применения алгоритмов, позволила выработать ряд конкретных требований, предъявляемых внутренней средой данной организации, и множество рекомендаций по повышению результативности труда конкретного объекта (испытуемого).

В случае с работой по анализу медицинских данных наиболее интересной оказалась такая возможность дублирования, как построение иерархической структуры зависимостей признаков. Такого рода иерархия помогает сформировать ряд приоритетных характеристик течения заболевания и их зависимость от других. Это позволило создать дополнительные знания и информационную поддержку для принятия решений о проведении своевременных профилактических мероприятий.

Однако предложенные алгоритмы дублирования не избавлены от недостатков. Некоторые из них являются достаточно трудоемкими и требуют от пользователя максимум внимания. Но данная проблема может быть частично устранена при соответствующей технической и аппаратной поддержке решения задачи.

Таким образом, в процессе проведения диссертационных исследований были достигнуты следующие основное научные результаты:

1. На основе анализа способов контроля достоверности данных показано, что в процессе решения задач минимизации описания в условиях появления искажений входной информации возникает проблема поиска компромисса, способного реализовать и цели минимизации, и цели сохранения устойчивости систем обработки данных к искажениям.

2. Проведен анализ различных подходов к решению задачи поиска набора входных параметров, обеспечивающих устойчивость решения к искажениям во входной информации. На его основе предложен метод дублирования, основанный на дополнении количества признаков минимального набора на соответствующие признаки с дублирующей информацией, и разработаны его теоретические основы.

3. Выделено четыре вида дублей (прямой дубль первого рода, косвенный дубль первого рода, прямой дубль второго рода и косвенный дубль второго рода). Построены алгоритмы их получения и показаны соотношения между различными видами дублей. Описанные алгоритмы могут быть применены как к нейронным сетям, так и к линейной и нелинейной регрессии.

4. На примере решения задач прогнозирования и классификации показано, что одновременное использование набора прототипов и дублеров позволяет формировать набор признаков, обладающий большей устойчивостью к искажениям информации во входных данных. Эксперименты показали, что в этих условиях менее устойчивой является нейросетевая система, решающая задачу на выборке с минимальным набором признаков, а более устойчивой – система, основанная на наборах повышенной надежности.

5. Анализ состава различных наборов признаков для конкретных задач классификации и прогнозирования проиллюстрировал, что ряд признаков не входит ни в минимальный набор, ни в набор дублеров. А анализ изменения ошибок вычисления показал, что эти признаки являются зашумляющими, то есть решение задачи осуществляется менее качественно, если они присутствуют в выборке.

Основное содержание диссертации изложено в следующих работах:

1.	Антамошкина О.И., Вашко Т.А. Нейронные сети в управлении персоналом//Достижения науки и техники – развитию сибирских регионов (инновационный и инвестиционный потенциалы): Материалы Всероссийской науч.-практ.конф. с междунар. участием: В 3ч. Ч. 3 Красноярск: КГТУ, 2000. - С. 49 – 51.
2.	Вашко Т.А. Дублирование информации в задаче прогнозирования результативности труда преподавателя//Вестник НИИ СУВПТ. - Красноярск: НИИ СУВПТ, 2001. – Вып. 7. – С. 165-173.
3.	Вашко Т.А. Нейронные сети в процессе анализа управленческой информации//Социально-экономические проблемы развития рынка потребительских товаров. Сборник тезисов региональной науч.-практич. конференции студентов и аспирантов. – Красноярск: КГТЭИ, изд-во КГПУ, 2000. – С. 148-149.
4.	Вашко Т.А. Нейросетевые подходы к обработке информации по отбору кадров//Вопросы менеджмента: Сб. науч. статей и тезисов. – Красноярск: КГТЭИ, изд-во КГПУ, 2000. – Вып. 2. - С.61-72.
5.	Вашко Т.А. Предпосылки возникновения идеи применения нейронных сетей в управлении персоналом//Вопросы менеджмента: Сб. науч. статей и тезисов. – Красноярск: КГТЭИ, изд-во КГПУ, 1998. – Вып. 1.- С.278–287.
6.	Вашко Т.А. Применение метода дублирования информации в задаче классификации осложнений инфаркта миокарда/Адаптивные системы управления и моделирования. - Красноярск: НИИ СУВПТ, 2000. - С.51-60.
7.	Вашко Т.А. Своевременная обработка информации как способ повышения конкурентоспособности фирмы//Экономические реформы в России. Материалы III Международной научно-практической конференции. – СПб.:Нестор, 2000. - С.93-95.
8.	Вашко Т.А. Специфика управленческой информации//Социально-экономические проблемы развития рынка потребительских товаров: Сб. тезисов региональной науч.-практич. конференции студентов и аспирантов. – Красноярск: КГТЭИ, изд-во КГПУ, 2000. – С. 144 -145.
9.	Горбань А.Н., Миркес Е.М., Вашко Т.А. Алгоритмы поиска дублирующих признаков/ ИВМ СО РАН - Красноярск, 2000. - 42 с. (Библиогр. 12 назв. Рус. – Деп. в ВИНИТИ 24.05.00 №1501-В00).
10.	Миркес Е.М., Вашко Т.А. Дублирование признаков как средство повышения надежности в процессе обработки информации//Вопросы менеджмента/Сб. науч. статей и тезисов. – Красноярск: КГТЭИ, изд-во КГПУ, 2000. – Вып. 2. - С. 173-185.
11.	Осипова Е.В., Вашко Т.А. Информационная система управления//Вопросы менеджмента/Сб. науч. статей и тезисов. – Красноярск: КГТЭИ, изд-во КГПУ, 2000. – Вып. 2. - С.220-223.

ЛИТЕРАТУРА

1. Айвазян С.А., Бежаева З.И., Староверов О.В. Классификация многомерных наблюдений. – М.: Статистика, 1974. – 240 с.

2. Айвазян С.А., Буштабер В.М., Енюков И.С. и др. Прикладная статистика. Классификация и снижение размерности. – М.: Финансы и статистика, 1989. – 607 с.

3. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Основы моделирования и первичная обработка данных. – М.: Финансы и статистика, 1983. – 471 с.

4. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Статистическое оценивание зависимостей. – М.: Финансы и статистика, 1985. – 484 с.

5. Александров В.В., Алексеев А.И., Горский Н.Д. Анализ данных на ЭВМ (на примере системы СИТО). – М.: Финансы и статистика, 1990. – 192 с.

6. Александров В.В., Шнейдеров В.С. Обработка медико-биологических данных на ЭВМ. – М.: Медицина, 1984. – 157 с.

7. Анастази А. Психологическое тестирование. – М. Педагогика, 1982 – кн.1 – 320 с., кн.2 – 360 с.

8. Андерсон Т. Введение в многомерный статистический анализ. - – М.: Финансы и статистика, 1963. – 500 с.

9. Анил К. Джейн, Жианчанг Мао, К.М. Моиуддин. Введение в искусственные нейронные сети // Открытые системы. — 1997 г., №4.

10. Антамошкина О.И., Вашко Т.А. Нейронные сети в управлении персоналом // Достижения науки и техники – развитию сибирских регионов (инновационный и инвестиционный потенциалы): Материалы Всероссийской науч.-практ.конф. с междунар. участием: В 3ч. Ч. 3 Красноярск: КГТУ, 2000. – С. 49 – 51.

11. Барабаш Б.А. Минимизация описания в задачах автоматического распознавания образов // Техн. Кибернетика, 1964, №3. – С. 32-44.

12. Борисов Ю., Кашкаров В., Сорокин С. Нейросетевые методы обработки информации и средства их программно-аппаратной поддержки // Открытые системы. — 1997 г., №4.

13. Браверман Э.М., Мучник И.Б. Структурные методы обработки эмпирических данных. – М.: Наука. Гл.ред.физ.-мат.лит., 1983. – 464 с.

14. Вайнцваг М.Н. Алгоритмы обучения распознаванию образов “Кора” // Алгоритмы обучения распознаванию образов. – М.: Сов. радио, 1973.

15. Вапник В.Н., Червоненкис А.Ф. Теория распознавания образов. – М.: Наука, 1988.

16. Васильев В.И. Распознающие системы. Справочник. – Киев: Наукова думка, 1983. – 422 с.

17. Вашко Т.А., Горбань А.Н., Миркес Е.М. Алгоритмы поиска дублирующих признаков/ ИВМ СО РАН - Красноярск, 2000. - 42 с. (Библиогр. 12 назв. Рус. – Деп. в ВИНИТИ 24.05.00 №1501-В00).

18. Вашко Т.А., Миркес Е.М. Дублирование признаков как средство повышения надежности в процессе обработки информации // Вопросы менеджмента/ Сборник научных статей и тезисов. – Красноярск: КГТЭИ, изд-во КГПУ, 2000. - С. 173-184.

19. Введение в информационный бизнес: Учебное пособие / Под ред. В.П.Тихомирова, А.В.Хорошилова. – М.: Финансы и статистика, 1996.

20. Галушкин А. Современные направления развития нейрокомпьютерных технологий в России // Открытые системы. — 1997 г., №4.

21. Гилев С.Е. Сравнение методов обучения нейронных сетей // Тез.докл. III Всероссийского семинара “Нейроинформатика и ее приложения”. – Красноярск: изд. КГТУ, 1995. – С. 80 – 81.

22. Гилев С.Е., Горбань А.Н., Миркес Е.М. и др. Определение значимости обучающих параметров для принятия нейронной сетью решения об ответе. // Нейроинформатика и нейрокомпьютеры: Тезисы докладов рабочего семинара, 8-11 октября 1993 г. – Красноярск: Институт биофизики СО РАН, 1993. – С.8.

23. Гилев С.Е., Коченов Д.А., Миркес Е.М., Россиев Д.А. Контрастирование, оценка значимости параметров, оптимизация их значений и их интерпретация в нейронных сетях // Тезисы докладов III всероссийского семинара “Нейроинформатика и ее приложения”. – Красноярск: изд. КГТУ, 1995 – С.66-78.

24. Гилев С.Е., Миркес Е.М. Обучение нейронных сетей // Эволюционное моделирование и кинетика. – Новосибирск: Наука. Сиб.отд-ие, 1992. - С. 9 – 23.

25. Горбань А.Н. Обучение нейронных сетей. – М. СП ПараГраф – 1990.

26. Горбань А.Н. Алгоритмы и программы быстрого обучения нейронных сетей // Эволюционное моделирование и кинетика. – Новосибирск: Наука. Сиб.отд-ие, 1992. - С. 36 – 39.

27. Горбань А.Н. Нейрокомпьютер или аналоговый ренессанс // МИР ПК, 1994, № 10.

28. Горбань А.Н. Обучение нейронных сетей.- М.: изд. USSR-USA JV “ParaGraph”, 1990.- 160 с. (англ. Перевод – Gorban A.N. Traning Neural Networks // AMSE Transaction, Scientific Siberian, A, 1993, V. 6. Neurocomputing, pp.1-134).

29. Горбань А.Н. Этот новый компьютерный мир. Заметки о нейрокомпьютерах и новой технической революции // Математическое обеспечение и архитектура ЭВМ: Материалы науч.-техн.конф. “Проблемы техники и технологий XXI века”, 22 – 25 марта 1994 г. – Красноярск: изд. КГТУ, 1994. – С. 6 – 9.

30. Горбань А.Н., Миркес Е.М. Кодирование качественных признаков для нейросетей // Тезисы докладов II всероссийского семинара “Нейроинформатика и ее приложения”. – Красноярск: изд. КГТУ, 1994 – С.29.

31. Горбань А.Н., Миркес Е.М. Контрастирование нейронных сетей. // Тезисы докладов III всероссийского семинара “Нейроинформатика и ее приложения”. – Красноярск: изд. КГТУ, 1995 – С.78-79.

32. Горбань А.Н., Россиев Д.А. Нейронные сети на персональном компьютере. Новосибирск: Наука, 1996. - 276 с.

33. Горбань А.Н., Фриденберг В.И. Новая игрушка человечества // МИР ПК, 1993, № 9.

34. Горелик А.Л. Гуревич И.Б., Скрипкин В.А. Современное состояние проблемы распознавания: Некоторые аспекты. – М.: Радио и связь, 1985.

35. Грановская Р.М., Березная И.Я. Интуиция и искусственный интеллект. – Л.: ЛГУ, 1991. – 272с.

36. Гублер Е.В. Информатика в патологии, клинической медицине и педиатрии. – Л.: Медицина, 1990. – 176 с.

37. Дейвисон М. Многомерное шкалирование: Методы наглядного представления данных. – М.: Финансы и статистика, 1988.

38. Демиденко Е.З. Линейная и нелинейная регрессия. – М.: Финансы и статистика, 1981. – 302 с.

39. Диго С.М. Проектирование баз данных. – М.: Финансы и статистика. 1988.

40. Дрейпер Н., Смит Г. Прикладной регрессионный анализ. – М.: Статистика, 1973. – 392 с.

41. Дуда Р., Харт П. Распознавание образов и анализ сцен. – М.: Мир, 1976.- 512 с.

42. Дюк В.А. Компьютерная психодиагностика. – Санкт-Петербург: Братство, 1994.

43. Елисеева И.И., Рукавишников В.О. Группировка, корреляция, распознавание образов (Статистические методы классификации и измерения связей). – М.: Статистика, 1977.

44. Енюков И.С. Методы, алгоритмы, программы многомерного статистического анализа: Пакет ППСА. – М.: Финансы и статистика, 1986.

45. Журавлев Ю.И. Непараметрические задачи распознавания образов // Кибернетика - №6 – 1976 – С.93-103.

46. Журавлев Ю.И. Об алгебраическом подходе к решению задач распознавания или классификации. // Проблемы кибернетики. М.: Наука, - 1978, вып. 33.

47. Журавлев Ю.И., Гуревич И.Б. Распознавание образов и анализ изображений // Искусственный интеллект. – В 3-х кн. Кн.2. – М.: Радио и связь, 1990 – С. 304.

48. Загоруйко Н.Г. Методы распознавания и их применение. – М.: Сов.радио, 1972. – 206 с.

49. Загоруйко Н.Г., Елкина В.Н., Лбов Г.С. Алгоритмы обнаружения эмпирических закономерностей. – Новосибирск: Наука, 1985 – 110с.

50. Зеличко А.И. Интеллектуальные системы и психологическое знание // в кн.: Компьютеры и познание. – М.: Наука, 1990. – С. 69-86.

51. Иберла К. Факторный анализ. – М.: Статистика, 1980. – 308 с.

52. Ивахненко А.Г. Персептроны. – Киев: Наукова думка, 1974.

53. Ивахненко А.Г. Самообучающиеся системы распознавания и автоматического регулирования. – Киев: Техника, 1969. – 392 с.

54. Ивахненко А.Г., Лапа В.Г. Кибернетические предсказывающие устройства. Киев, - Наукова думка, - 1965.

55. Информатика: Учебник / Под ред. Проф. Н.В.Макаровой. – М.: Финансы и статистика, 1997. – 768 с.: ил.

56. Информационные системы в экономике. – М.: Финансы и статистика, 1996.

57. Искусственный интеллект: В 3-х кн. Кн. 2. Модели и методы: Справочник / под ред. Д.А. Поспелова.- М.: Радио и связь, 1990.- 304 с.

58. Кабанов М.М., Личко А.И., Смирнов В.М. Методы психологической диагностики и коррекции в клинике. М. Медицина – 1983

59. Колмогоров А.Н. Три подхода к определению понятия “количество информации” // Проблемы передачи информации / под.ред. Яглома П.С., 1965, т.1, вып.1.

60. Кузнецов А.С. Методы поиска оптимальных групп признаков при статистическом распознавании образов. – Л.: ВИКИ им. А.Ф.Можайского, 1982. – С. 14-23.

61. Кулагин Б.В., Сергеев С.Т. Типологический подход к исследованию проблемы профотбора // Психологический журнал, 1989, т.10, №1

62. Лбов Г.С. Выбор эффективной системы зависимых признаков / Труды Сиб.отд. АН СССР: Вычислительные системы. – Новосибирск, 1965, вып. 19. – С. 87 – 101.

63. Лбов Г.С. Логические функции в задачах эмпирического предсказания // Эмпирическое предсказание и распознавание образов: Вычислительные системы. – Новосибирск, 1978, вып. 76. – С. 34 – 64.

64. Лбов Г.С. Методы обработки разнотипных экспериментальных данных. – Новосибирск: Наука, 1981. – 157 с.

65. Лоули Д., Максвелл А. Факторный анализ как статистический метод. – М.: Мир, 1967. – С. 10-17.

66. Мак-Карти, Шеннон (ред.). Автоматы – ИЛ – 1956.

67. Максимов М.М. Модульные интегрированные системы управления объектами информационного производства. – М.: Информприбор, 1989.

68. Масалович А. Нейронная сеть – оружие финансиста. – PC WEEK, - 24.04.1995.

69. Матвеев Л.А. Информационные системы: поддержка принятия решений: Учебное пособие. – СПб.: Изд-во СПбУЭФ, 1996.

70. Мельников В.М., Ямпольский Л.Т. Введение в экспериментальную психологию личности. – М.: Просвещение, 1985. – 319 с.

71. Минский М., Пайперт С. Персептроны. – М.: Мир, 1971.

72. Миркин Б.Г. Анализ качественных признаков и структур. – М.: Финансы и статистика, 1980. – 319 с.

73. Мостеллер Ф., Тьюки Дж. Анализ данных и регрессия. – М.: Финансы и статистика, 1982.- 239 с.

74. Налимов В.В. Теория эксперимента. – М: Наука, 1971.

75. Нейронные сети на персональном компьютере / А.Н.Горбань, Д.А.Россиев. – Новосибирск: Наука. Сибирская издательская фирма РАН, 1996. – 276 с.

76. Нейропрограммы / сборник статей под ред. А.Н. Горбаня //Красноярск, КГТУ, 1994.

77. Нейропрограммы. Учебное пособие: В двух частях / Под. Ред. А.Н.Горбаня. Красноярск: изд. КГТУ, 1994. Часть 1.- 137 с. Часть 2.- 123 с.

78. Никифоров А.М., Фазылов Ш.Х. Методы и алгоритмы преобразования типов признаков в задачах анализа данных. – Ташкент: Фан, 1988. – 132с.

79. Нильсон Н. Принципы искусственного интеллекта. – М.: Радио и связь, 1985.

80. Общая теория статистики: Учебник/А.Я.Боярский, Л.Л.Викторова, А.М.Гольдберг и др.; Под ред. А.М.Гольдберга, В.С.Козлова. – М.: Финансы и статистика, 1985. – 367 с. ил.

81. Патрик Э. Основы теории распознавания образов. – М.: Сов.радио, 1970. – 408 с.

82. Поспелов Д.А. Данные и знания. Представление знаний // Искусственный интеллект. Кн.2: Модели и методы: Справочник – М.: Радио и связь. – С.7-13.

83. Поспелов Д.А. Искусственный интеллект: фантазия или наука? – М.: Радио и связь, 1986.

84. Ракитов А.И. Философия компьютерной революции. – М.: Политическая литература, 1990.

85. Распознавание образов и медицинская диагностика / под.ред. Неймарка Ю.М. – М.: Наука, 1972. – 328 с.

86. Решетников М.М. Профессиональный отбор в системе образования, промышленности и армии США // Психолог.журн., т. 8, № 3, 1987. – С. 81 – 119.

87. Розенблатт Ф. Принципы нейродинамики. Перцептрон и теория механизмов мозга. – М.: Мир, 1965. – 480 с.

88. Россиев Д.А. Нейросетевые самообучающиеся экспертные системы в медицине // Молодые ученые – практическому здравоохранению. – Красноярск, 1994. – С. 17.

89. Россиев Д.А., Головенкин С.Е., Назаров Б.В. и др. Определение информативности медицинских параметров с помощью нейронной сети // Диагностика, информатика и метрология – 94: Тезисы науч.-техн. конференции, Санкт-Петербург, 28-30 июня 1994 г. – С-Пб., 1994. – С.348.

90. Справочник по искусственному интеллекту в 3-х тт./Под ред. Попова Э.В. и Поспелова Д.А. – М.: Радио и связь, 1990.

91. Справочник по прикладной статистике. В 2-х т. / Под.ред. Ллойда Э., Ледермана У., Айвазяна С.А., Тюрина Ю.Н. – М.: Финансы и статистика, 1990.

92. Терехина А.Ю. Анализ данных методами многомерного шкалирования. – М.: Наука, 1986. – 168 с.

93. Уинстон П. Искусственный интеллект. – М.: Мир, 1980.

94. Уоссермен Ф. Нейрокомпьютерная техника. – М.: Мир, 1992 – 126 с.

95. Федеральный закон “Об информации, информатизации и защите информации”. Принят Государственной Думой 25 января 1995 г.

96. Фогель Л., Оуэнс А., Уолш М. Искусственный интеллект и эволюционное моделирование. – М.: Мир, 1969. – 230 с.

97. Фор А. Восприятие и распознавание образов. – М.: Машиностроение, 1989.- 272 с.

98. Фу. К. Структурные методы в распознавании образов. – М. Мир, 1977.

99. Харман Г. Современный факторный анализ. – М.: Статистика, 1972.

100. Хетагуров В.А. Синтез алгоритмов дискриминации в условиях статистической неопределенности данных для автоматизированной медицинской диагностики. – Автореф.дисс. на соиск.уч.ст.канд.техн.наук. – М., 1985. – 19 с.

101. Цыпкин Я.З. Адаптация и обучение в автоматических системах. – М.: Наука, 1968. – 400 с.

102. Шеметов Д.В., Осипов Ю.М. Определение показателя “значимость технического решения” аппаратом нейронных сетей./ Нейроинформатика и ее приложения: Тезисы доклада VI Всероссийского семинара, 2-5 октября 1998г. Красноярск, 1998. – С. 190-191.

103. Asary K.V., Eswaran C.A. Self-organizing Neural Network for Multidimensional Mapping and Classification of Multiple Valued Data // Proceedings of 1993 International Joint Conference on Neural Networks, Nagoya, Japan, October 25-29, 1993. – Nagoya, 1993. – v.2. – p.2488-2491.

104. Becraft W.R. Diagnostic applications of artificial neural networks // Proceedings of 1993 International Joint Conference on Neural Networks, Nagoya, Japan, October 25-29, 1993. – Nagoya, 1993. – v.2. – p.2807-2810.

105. Cover T., Hart P. Nearest neighbour pattern classification // IEEE Trans. Inform. Theory, v. IT – 13, 1967. – p. 21 – 27.

106. Fix E., Hodges J.L. Discriminatory analysis, nonparametric discrimination USA School of Medicine, - Texas: Rendolph Field, 1951 – 1952.

107. Forrest D.V., Flory M.J., Anderson S. Neural network programming // N.Y.State J. Med. – 1991. – v.91, №12. – p.553.

108. Fu H.C., Shann J.J. A fuzzy neural network for knowledge learning // Int. J. Neural Syst. – 1994. – v.5, №1. – p.13-22.

109. Galushkin A.I., Sudarikov V.A., Shabanov E.V. Neuromathematic: the methods of solving problems on neurocomputers // The RNNS-IEEE Symposium on Neuroinformatics and Neurocomputers, Rostov-on-Don, September 1992 – v.2. – pp 1179-1188.

110. Sitting D.F., Orr J.A. A parallel implementation of the backward error propagation neural network training algorithm: experiments in event identification // Comput. Biomed Res. – 1992. – v.25, №6. – p.547-561.

ПРИЛОЖЕНИЕ 1.
Набор признаков для прогнозирования летального исхода в случае инфаркта миокарда

1. Фамилия Имя Отчество (FIO).

2. Возраст (AGE).

3. Пол (SEX):

a) 0 – женский,

b) 1 – мужской.

4. Количество инфарктов миокарда в анамнезе (INF_ANAM):

a) 0 – нет,

b) 1 – один,

c) 2 – два,

d) 3 – три и. т.д.

5. Стенокардия напряжения в анамнезе (STENOK_AN):

a) 0 – нет,

b) 1 – менее 1 года,

c) 2 – один год,

d) 3 – два года,

e) 4 – три года,

f) 5 – 4-5 лет,

g) 6 – более 5 лет.

6. Функциональный класс стенокардии в последний год (FK_STENOK):

a) 0 – нет стенокардии,

b) 1 – I ф.к.,

c) 2 – II ф.к.,

d) 3 – III ф.к.,

e) 4 – IV ф.к.

7. Характер ИБС в последние недели, дни перед поступлением в больницу (IBS_POST):

a) 0 – нет ИБС,

b) 1 – стенокардия напряжения,

c) 2 – нестабильная стенокардия.

9. Наличие гипертонической болезни (GB):

a) 0 – нет Г.Б.,

b) 1 – I стадия Г.Б.,

c) 2 – II стадия Г.Б.,

d) 3 – III стадия Г.Б.

10. Симптоматическая гипертония (SIM_GIPERT):

a) 0 – нет,

b) 1 – да.

11. Длительность течения арт. Гипертензии (DLIT_AG):

a) 0 – нет А.Г.,

b) 1 – год,

c) 2 – два года,

d) 3 – три года,

e) 4 – четыре года,

f) 5 – пять лет,

g) 6 – 5-10 лет,

h) 7 – более 10 лет.

12. Наличие хронической сердечной недостаточности (СН) в анамнезе (ZSN_A):

a) 0 – нет,

b) 1 – I стадии,

c) 2 – IIА стадия (застой по большому кругу),

d) 3 – IIА стадия (застой по малому кругу),

e) 4 – IIБ стадия,

f) 5 – III стадия.

13. Нарушения ритма в анамнезе, не уточнено какие именно (nr11):

a) 0 – нет,

b) 1 – да.

14. Предсердная экстрасистолия в анамнезе (nr01):

a) 0 – нет,

b) 1 – да.

15. Желудочковая экстрасистолия в анамнезе (nr02):

a) 0 – нет,

b) 1 – да.

16. Пароксизмы фибрилляции/трепетании предсердий в анамнезе (nr03):

a) 0 – нет,

b) 1 – да.

17. Постоянная форма фибрилляции предсердий в анамнезе (nr04):

a) 0 – нет,

b) 1 – да.

18. Желудочковая пароксизмальная тахикардия в анамнезе (nr05):

a) 0 – нет,

b) 1 – да.

19. Фибрилляция желудочков в анамнезе (nr07):

a) 0 – нет,

b) 1 – да.

20. А-в блокада I степени в анамнезе (np01):

a) 0 – нет,

b) 1 – да.

21. А-в блокада III степени в анамнезе (np04):

a) 0 – нет,

b) 1 – да.

22. Блокада передней ветви левой ножки пучка Гиса в анамнезе (np05):

a) 0 – нет,

b) 1 – да.

23. Неполная блокада левой ножки пучка Гиса в анамнезе (np07):

a) 0 – нет,

b) 1 – да.

24. Полная блокада левой ножки пучка Гиса в анамнезе (np08):

a) 0 – нет,

b) 1 – да.

25. Неполная блокада правой ножки пучка Гиса в анамнезе (np09):

a) 0 – нет,

b) 1 – да.

26. Полная блокада правой ножки пучка Гиса в анамнезе (np10):

a) 0 – нет,

b) 1 – да.

27. Сахарный диабет в анамнезе (endocr_01):

a) 0 – нет,

b) 1 – да.

28. Ожирение в анамнезе (endocr_02):

a) 0 – нет,

b) 1 – да.

29. Тиреотоксикоз в анамнезе (endocr_03):

a) 0 – нет,

b) 1 – да.

30. Хронический бронхит в анамнезе (zab_leg_01):

a) 0 – нет,

b) 1 – да.

31. Обструктивный хронический бронхит в анамнезе (zab_leg_02):

a) 0 – нет,

b) 1 – да.

32. Бронхиальная астма в анамнезе (zab_leg_03):

a) 0 – нет,

b) 1 – да.

33. Хроническая пневмония в анамнезе (zab_leg_04):

a) 0 – нет,

b) 1 – да.

34. Туберкулез легкого (легких) в анамнезе (zab_leg_06):

a) 0 – нет,

b) 1 – да.

37. Систолическое. АД по данным ОриИТ (S_AD_ORIT).

38. Диастолическое. АД по данным ОриИТ (D_AD_ORIT).

39. Отек легких в момент поступления в ОриИТ: (O_L_POST):

a) 0 – нет,

b) 1 – да.

40. Кардиогенный шок в момент поступления в ОриИТ (K_SH_POST):

a) 0 – нет,

b) 1 – да.

41. Пароксизм фибрилляции предсердий (ТП) в момент поступления в ОриИТ, (или на догоспитальном этапе) (MP_TP_POST):

a) 0 – нет,

b) 1 – да.

42. Пароксизм суправентрикулярной тахикардии в момент поступления в ОриИТ, (или на догоспитальном этапе) (SVT_POST):

a) 0 – нет.

b) 1 – да.

43. Пароксизм желудочковой тахикардии в момент поступления в ОриИТ, (или на догоспитальном этапе) (GT_POST):

a) 0 – нет,

b) 1 – да.

44. Фибрилляция желудочков в момент поступления в ОриИТ, (или на догоспитальном этапе) (FIB_G_POST):

a) 0 – нет,

b) 1 – да.

45. Наличие инфаркта передней стенки левого желудочка (изменения на ЭКГ в отведениях V2 – V4) (ant_im):

a) 0 – нет,

b) 1 – форма комплекса QRS не изменена,

c) 2 – форма QRS комплекса QR,

d) 3 – форма QRS комплекса Qr,

e) 4 – форма QRS комплекса QS.

46. Наличие инфаркта боковой стенки левого желудочка (изменения на ЭКГ в отведениях V5 – V6, I, AVL (lat_im):

a) 0 – нет,

b) 1 – форма комплекса QRS не изменена,

c) 2 – форма QRS комплекса QR,

d) 3 – форма QRS комплекса Qr,

e) 4 – форма QRS комплекса QS.

47. Наличие инфаркта нижней стенки левого желудочка (изменения на ЭКГ в отведениях III, AVF, II) (inf_im):

a) 0 – нет,

b) 1 – форма комплекса QRS не изменена,

c) 2 – форма QRS комплекса QR,

d) 3 – форма QRS комплекса Qr,

e) 4 – форма QRS комплекса QS.

48. Наличие инфаркта задней стенки левого желудочка (изменения на ЭКГ в отведениях V7-V9, реципрокные изменения в отведениях V1-V3) (post_im):

a) 0 – нет,

b) 1 – форма комплекса QRS не изменена,

c) 2 – форма QRS комплекса QR,

d) 3 – форма QRS комплекса Qr,

e) 4 – форма QRS комплекса QS.

49. Наличие ИМ правого желудочка (IM_PG_P):

a) 0 – нет,

b) 1 – да.

50. Ритм по ЭКГ при поступлении – синусовый (с чсс 60-90 в мин.) (ritm_ecg_p_01):

a) 0 – нет,

b) 1 – да.

51. Ритм по ЭКГ при поступлении – фибрилляция предсердий (ritm_ecg_p_02):

a) 0 – нет,

b) 1 – да.

52. Ритм по ЭКГ при поступлении – предсердный (ritm_ecg_p_04):

a) 0 – нет,

b) 1 – да.

53. Ритм по ЭКГ при поступлении – идиовентрикулярный (ritm_ecg_p_06):

a) 0 – нет,

b) 1 – да.

54. Ритм по ЭКГ при поступлении – синусовый с ЧСС более 90 в мин. (синусовая тахикардия) (ritm_ecg_p_07):

a) 0 – нет,

b) 1 – да.

55. Ритм по ЭКГ при поступлении – синусовый с ЧСС менее 60 в мин. (синусовая брадикардия) (ritm_ecg_p_08):

a) 0 – нет,

b) 1 – да.

56. Предсердная экстросистолия на ЭКГ при поступлении (n_r_ecg_p_01):

a) 0 – нет,

b) 1 – да.

57. Частая предсердная экстросистолия на ЭКГ при поступлении (n_r_ecg_p_02):

a) 0 – нет,

b) 1 – да.

58. Желудочковая экстросистолия на ЭКГ при поступлении (n_r_ecg_p_03):

a) 0 – нет,

b) 1 – да.

59. Частая желудочковая экстросистолия на ЭКГ при поступлении (n_r_ecg_p_04):

a) 0 – нет,

b) 1 – да.

60. Пароксизмы фибрилляции предсердий на ЭКГ при поступлении (n_r_ecg_p_05):

a) 0 – нет,

b) 1 – да.

61. Постоянная форма фибрилляции предсердий на ЭКГ при поступлении (n_r_ecg_p_06):

a) 0 – нет,

b) 1 – да.

62. Суправентрикулярная пароксизмальная тахикардия на ЭКГ при поступлении (n_r_ecg_p_08):

a) 0 – нет,

b) 1 – да.

63. Желудочковая пароксизмальная тахикардия на ЭКГ при поступлении (n_r_ecg_p_09):

a) 0 – нет,

b) 1 – да.

64. Фибрилляция желудочков на ЭКГ при поступлении (n_r_ecg_p_10):

a) 0 – нет,

b) 1 – да.

65. Синоатриальная блокада на ЭКГ при поступлении (n_p_ecg_p_01):

a) 0 – нет,

b) 1 – да.

66. А-В блокада I степени на ЭКГ при поступлении (n_p_ecg_p_03):

a) 0 – нет,

b) 1 – да.

67. А-В блокада II степени I типа на ЭКГ при поступлении (n_p_ecg_p_04):

a) 0 – нет,

b) 1 – да.

68. А-В блокада II степени II типа на ЭКГ при поступлении (n_p_ecg_p_05):

a) 0 – нет,

b) 1 – да.

69. А-В блокада III степени на ЭКГ при поступлении (n_p_ecg_p_06):

a) 0 – нет,

b) 1 – да.

70. Блокада передней ветви левой ножки пучка Гиса на ЭКГ при поступлении (n_p_ecg_p_07):

a) 0 – нет,

b) 1 – да.

71. Блокада задней ветви левой ножки пучка на ЭКГ при поступлении (n_p_ecg_p_08):

a) 0 – нет,

b) 1 – да.

72. Неполная блокада левой ножки пучка Гиса на ЭКГ при поступлении (n_p_ecg_p_09):

a) 0 – нет,

b) 1 – да.

73. Полная блокада левой ножки пучка Гиса на ЭКГ при поступлении (n_p_ecg_p_10):

a) 0 – нет,

b) 1 – да.

74. Неполная блокада правой ножки пучка Гиса на ЭКГ при поступлении (n_p_ecg_p_11):

a) 0 – нет,

b) 1 – да.

75. Полная блокада правой ножки пучка Гиса на ЭКГ при поступлении (n_p_ecg_p_12):

a) 0 – нет,

b) 1 – да.

76. Проведение фибринолитической терапии целиазой 750 тыс. ЕД (fibr_ter_01):

a) 0 – нет,

b) 1 – да.

77. Проведение фибринолитической терапии целиазой 1 млн. ЕД (fibr_ter_02):

a) 0 – нет,

b) 1 – да.

78. Проведение фибринолитической терапии стрептодеказой 3 млн. ЕД (fibr_ter_03):

a) 0 – нет,

b) 1 – да.

79. Проведение фибринолитической терапии стрептазой (fibr_ter_05):

a) 0 – нет,

b) 1 – да.

80. Проведение фибринолитической терапии целиазой 500 тыс. ЕД (fibr_ter_06):

a) 0 – нет,

b) 1 – да.

81. Проведение фибринолитической терапии целиазой 250 тыс. ЕД (fibr_ter_07):

a) 0 – нет,

b) 1 – да.

82. Проведение фибринолитической терапии стрептодеказой 1,5 млн. ЕД (fibr_ter_08):

a) 0 – нет,

b) 1 – да.

83. Гипокалиемия ( < 4 ммоль/л ) (GIPO_K):

a) 0 – нет,

b) 1 – да.

84. Содержание К⁺ в сыворотке крови (K_BLOOD).

85. Увеличение Na в сыворотке крови (более 150 ммоль/л) (GIPER_Na):

a) 0 – нет,

b) 1 – да.

86. Содержание Na в сыворотке крови (Na_BLOOD).

87. Содержание АлАТ в крови (ALT_BLOOD).

88. Содержание АсАТ в крови (AST_BLOOD).

90. Содержание лейкоцитов в крови (´10⁹ /л ) (L_BLOOD).

91. СОЭ (скорость оседания эритроцитов) (ROE).

92. Время, прошедшее от начала ангинозного приступа до поступления в стационар (TIME_B_S):

a) 1 – менее 2 часов,

b) 2 – 2-4 часа,

c) 3 – 4-6 часов,

d) 4 – 6-8 часов,

e) 5 – 8-12 часов,

f) 6 – 12-24 часов,

g) 7 – более 1 суток,

h) 8 – более 2 суток,

i) 9 – более 3 суток.

93. Повышение температуры в первые сутки (TEMPER_1_N):

a) 0 – нет,

b) 1 – 37-37,5°,

c) 2 – 37,5-38°,

d) 3 – 38-38,5°,

e) 4 – 38,5-39°,

f) 5 – 39-39,5°,

g) 6 - >39,5°.

94. Повышение температуры во вторые сутки (TEMPER_2_N):

a) 0 – нет,

b) 1 – 37-37,5°,

c) 2 – 37,5-38°,

d) 3 – 38-38,5°,

e) 4 – 38,5-39°,

f) 5 – 39-39,5°,

g) 6 - >39,5°.

95. Повышение температуры в третьи сутки (TEMPER_3_N):

a) 0 – нет,

b) 1 – 37-37,5°,

c) 2 – 37,5-38°,

d) 3 – 38-38,5°,

e) 4 – 38,5-39°,

f) 5 – 39-39,5°,

g) 6 - >39,5°.

96. Рецидивирование ангинозных болей в 1-е сутки стац. Лечения (R_AB_1_N):

a) 0 – не рецидивировали,

b) 1 – однократно,

c) 2 – 2 раза,

d) 3 – 3 раза и т.д.

97. Рецидивирование ангинозных болей во 2-е сутки стац. Лечения (R_AB_2_N):

a) 0 – не рецидивировали,

b) 1 – однократно,

c) 2 – более 1-го раза.

98. Рецидивирование ангинозных болей в 3-и сутки стац. Лечения (R_AB_3_N):

a) 0 – не рецидивировали,

b) 1 – однократно,

c) 2 – более 1-го раза.

102. Применение жидких нитратов в ОриИТ (NITR_S):

a) 0 – нет,

b) 1 – да.

103. Применение наркотических анальгетиков в ОриИТ в 1 сутки (NA_R_1_N):

a) 0 – не вводились,

b) 1 – вводились однократно,

c) 2 – вводились двукратно,

d) 3 – вводились 3-х кратно,

e) 4 – вводились 4-х кратно.

104. Применение наркотических анальгетиков в ОриИТ во 2 сутки (NA_R_2_N):

a) 0 – не вводились,

b) 1 – вводились однократно,

c) 2 – вводились более 1 раза.

105. Применение наркотических анальгетиков в ОриИТ в 3 сутки (NA_R_3_N):

a) 0 – не вводились,

b) 1 – вводились однократно,

c) 2 – вводились более 1 раза.

106. Применение ненаркотических анальгетиков в ОриИТ в 1 сутки (NOT_NA_1_N):

a) 0 – не вводились,

b) 1 – вводились однократно,

c) 2 – вводились двукратно,

d) 3 – вводились 3-х кратно,

e) 4 – вводились 4-х кратно и т.д.

107. Применение ненаркотических анальгетиков в ОриИТ во 2 сутки (NOT_NA_2_N):

a) 0 – не вводились,

b) 1 – вводились однократно,

c) 2 – вводились более 1 раза.

108. Применение ненаркотических анальгетиков в ОриИТ в 3 сутки (NOT_NA_3_N):

a) 0 – не вводились,

b) 1 – вводились однократно,

c) 2 – вводились более 1 раза.

109. Введение лидокаина в ОриИТ (LID_S_N):

a) 0 – нет,

b) 1 – да.

110. Прием блокаторов в ОриИТ (B_BLOK_S_N):

a) 0 – нет,

b) 1 – да.

111. Прием антагонистов Са в ОриИТ (ANT_Ca_S_N):

a) 0 – нет,

b) 1 – да.

112. Введение антикоагулянтов (гепарин) (GEPAR_S_N):

a) 0 – нет,

b) 1 – да.

113. Прием аспирина (ASP_S_N):

a) 0 – нет,

b) 1 – да.

114. Прием тиклида (TIKL_S_N):

a) 0 – нет,

b) 1 – да.

115. Прием трентала (TRENT_S_N):

a) 0 – нет,

b) 1 – да.

116. Фибрилляция/трепетание предсердий (FIBR_PREDS):

a) 0 – нет,

b) 1 – да.

117. Суправентрикулярная тахикардия (PREDS_TAH):

a) 0 – нет,

b) 1 – да.

118. Желудочковая тахикардия (JELUD_TAH):

a) 0 – нет,

b) 1 – да.

119. Фибрилляция желудочков (FIBR_JELUD):

a) 0 – нет,

b) 1 – да.

120. Полная а-в блокада (A_V_BLOK):

a) 0 – нет,

b) 1 – да.

121. Отек легких (OTEK_LANC):

a) 0 – нет,

b) 1 – да.

122. Разрыв сердца (RAZRIV):

a) 0 – нет,

b) 1 – да.

123. Синдром Дресслера (DRESSLER):

a) 0 – нет,

b) 1 – да.

124. Хроническая сердечная недостаточность (ZSN):

a) 0 – нет,

b) 1 – да.

125. Рецидив инфаркта миокарда (REC_IM):

a) 0 – нет,

b) 1 – да.

126. Постинфарктная стенокардия (P_IM_STEN):

a) 0 – нет,

b) 1 – да.

ПРИЛОЖЕНИЕ 2.
Характеристика классов осложнений инфаркта миокарда – летальный исход (LET_IS)

Класс	Значение	Характеристика
Класс 1	0	Нет
Класс 2	1	Кардиогенный шок
Класс 3	2	Отек легких
Класс 4	3	Разрыв миокарда
Класс 5	4	Прогрессирование застойной сердечной недостаточности
Класс 6	5	Тромбоэмболия
Класс 7	6	Асистолия
Класс 8	7	Фибрилляция желудочков

ПРИЛОЖЕНИЕ 3.
Результаты экспериментов по реализации
алгоритмов дублирования при решении задачи
прогнозирования осложнений инфаркта миокарда

Таблица 1

Наборы признаков на базе реализации алгоритма поиска ПДПР

Порядковый номер признака (описание см. в прил. 1)	Вид набора признаков
Порядковый номер признака (описание см. в прил. 1)	Набор прототипов	Набор дублеров	Набор повышенной надежности
1	2	3	4
2
3	*		*
4		*	*
5
6
7		*	*
8
9
10
11
12	*		*
13
14
15	*		*
16		*	*
17		*	*
18
19		*	*
20
21	*		*
22	*		*
23
24	*		*
25
26
27
28	*		*
29		*	*
30	*		*
31	*		*
32
33	*		*
34	*		*
35
36

Продолжение таблицы 1

1	2	3	4
37
38
39	*		*
40	*		*
41	*		*
42
43	*		*
44	*		*
45		*	*
46
47		*	*
48		*	*
49	*		*
50		*	*
51	*		*
52	*		*
53
54		*	*
55		*	*
56
57	*		*
58
59
60	*		*
61	*		*
62
63
64
65
66	*		*
67
68
69	*		*
70	*		*
71	*		*
72
73	*		*
74
75	*		*
76	*		*
77	*		*
78		*	*
79
80
81
82
83	*		*

Продолжение таблицы 1

1	2	3	4
84
85	*		*
86
87		*	*
88	*		*
89
90
91	*		*
92		*	*
93
94
95
96	*		*
97		*	*
98	*		*
99
100
101
102	*		*
103	*		*
104		*	*
105	*		*
106		*	*
107		*	*
108		*	*
109	*		*
110
111	*		*
112	*		*
113
114	*		*
115		*	*
116		*	*
117
118		*	*
119	*		*
120		*	*
121	*		*
122	*		*
123	*		*
124	*		*
125	*		*
126	*		*
Количество признаков в наборе	50	24	74

* - признак входит в состав набора

Таблица 2

Результаты тестирования нейронной сети на выборке М-М’ в процессе реализации алгоритма построения КДПР

Порядковый номер признака-прототипа	Тестируемый параметр
Порядковый номер признака-прототипа	Правильно	Неуверенно	Неправильно
1	2	3	4
3	38 (7,0 %)	303 (57,0%)	188 (36,0%)
12	215 (41,0%)	257 (48,0 %)	57 (11,0%)
15	523 (98,5%)	0 (0%)	6 (1,5%)
21	528 (99,8%)	0 (0%)	1 (0,2%)
22	518 (98,0%)	9 (1,7%)	2 (0,3%)
24	528 (99,8%)	0 (0%)	1 (0,2%)
28	515 (97,5%)	3 (0,5%)	11 (2,0%)
30	119 (22,5%)	374 (70,7%)	36 (6,8%)
31	205 (38,8%)	293 (55,4%)	31 (5,8%)
33	527 (99,6%)	1 (0,2%)	1 (0,2%)
34	524 (99,1%)	0 (0%)	5 (0,9%)
39	255 (48,2%)	238 (45,0%)	36 (6,8%)
40	528 (99,8%)	0 (0%)	1 (0,2%)
41	499 (94,3%)	21 (4,0%)	9 (1,7%)
43	528 (99,8%)	0 (0%)	1 (0,2%)
44	492 (93,0%)	33 (6,2%)	4 (0,8%)
49	412 (77,9%)	102 (19,3%)	15 (2,8%)
51	507 (95,8%)	16 (3,1%)	6 (1,1%)
52	505 (95,5%)	19 (3,6%)	5 (0,9%)
57	528 (99,8%)	0 (0%)	1 (0,2%)
60	462 (87,5%)	51 (9,6%)	16 (3,1%)
61	517 (97,7%)	8 (1,5%)	4 (0,8%)
66	488 (92,3%)	34 (6,4%)	7 (1,3%)
69	487 (92,1%)	36 (6,8%)	6 (1,1%)
70	463 (87,5%)	43 (8,1%)	23 (4,4%)
71	507 (95,8%)	18 (3,4%)	4 (0,8%)
73	483 (91,3%)	40 (7,6%)	6 (1,1%)
75	311 (58,8%)	192 (36,3%)	26 (4,9%)
76	528 (99,8%)	0 (0%)	1 (0,2%)
77	478 (90,4%)	43 (8,1%)	8 (1,5%)
83	0 (0%)	301 (56,9%)	228 (43,1%)
85	510 (96,4%)	7 (1,3%)	12 (2,2%)
88	60 (11,3%)	422 (79,8%)	47 (8,9%)

Продолжение таблицы 2

1	2	3	4
91	381 (72,1%)	0(0%)	148 (27,9%)
96	14 (2,6%)	392 (74,1%)	123 (23,3%)
98	295 (55,8%)	206 (38,9%)	28 (5,3%)
102	191 (36,1%)	278 (52,6%)	60 (11,3%)
103	0 (0%)	355 (67,1%)	174 (32,9%)
105	373 (70,5%)	134 (25,3%)	22 (4,2%)
109	1 (0,2%)	359 (67,9%)	169 (31,9%)
111	1 (0,2%)	389 (73,5%)	139 (26,3%)
112	0 (0%)	426 (80,5%)	103 (19,5%)
114	451 (85,3%)	65 (12,3%)	13 (2,4%)
119	389 (73,5%)	120 (22,7%)	20 (3,8%)
121	251 (47,5%)	227 (42,9%)	51 (9,6%)
122	393 (74,3%)	118 (22,3%)	18 (3,4%)
123	109 (20,6%)	387 (73,2%)	33 (6,2%)
124	75 (14,2%)	300 (56,7%)	154 (29,1%)
125	144 (27,2%)	340 (64,3%)	45 (8,5%)
126	58 (10,9%)	430 (81,3%)	41 (7,8%)

Таблица 5

Анализ степени участия признаков в различных видах наборов

Порядковый номер признака	Вид набора				Наличие признака в наборах, (“+”-есть, “-” - нет)
Порядковый номер признака	Минимальный набор	Прямой дубль первого рода	Прямой дубль второго рода	Косвенный дубль второго рода	Наличие признака в наборах, (“+”-есть, “-” - нет)
1	2	3	4	5	6
2					-
3	*		*	*	+
4		*	*	*	+
5			*	*	+
6				*	+
7		*	*	*	+
9			*	*	+
10			*	*	+
11			*	*	+
12	*		*	*	+
13			*	*	+
14			*	*	+
15	*		*	*	+
16		*	*	*	+
17		*	*	*	+
18					-
19		*	*	*	+
20					-
21	*		*	*	+
22	*		*	*	+
23					-
24	*		*	*	+
25					-
26					-
27			*	*	+
28	*		*	*	+
29		*	*	*	+
30	*		*	*	+
31	*		*	*	+
32			*	*	+
33	*		*	*	+
34	*		*	*	+
37					-
38					-
39	*		*	*	+
40	*		*	*	+

Продолжение таблицы 5

1	2	3	4	5	6
41	*		*	*	+
42					-
43	*		*	*	+
44	*		*	*	+
45		*	*	*	+
46			*	*	+
47		*	*	*	+
48		*	*	*	+
49	*		*	*	+
50		*	*	*	+
51	*		*	*	+
52	*		*	*	+
53					-
54		*	*	*	+
55		*	*	*	+
56			*	*	+
57	*		*	*	+
58			*	*	+
59			*	*	+
60	*		*	*	+
61	*		*	*	+
62					-
63					-
64					-
65					-
66	*		*	*	+
67					-
68					-
69	*		*	*	+
70	*		*	*	+
71	*		*	*	+
72					-
73	*		*	*	+
74			*	*	+
75	*		*	*	+
76	*		*	*	+
77	*		*	*	+
78		*	*	*	+
79			*	*	+
80			*	*	+
81			*	*	+
82					-
83	*		*	*	+
84				*	+

Продолжение таблицы 5

1	2	3	4	5	6
85	*		*	*	+
86				*	+
87		*	*	*	+
88	*		*	*	+
90			*	*	+
91	*		*	*	+
92		*	*	*	+
93			*	*	+
94			*	*	+
95			*	*	+
96	*		*	*	+
97		*	*	*	+
98	*		*	*	+
102	*		*	*	+
103	*		*	*	+
104		*	*	*	+
105	*		*	*	+
106		*	*	*	+
107		*	*	*	+
108		*	*	*	+
109	*		*	*	+
110			*	*	+
111	*		*	*	+
112	*		*	*	+
113			*	*	+
114	*		*	*	+
115		*	*	*	+
116		*	*	*	+
117			*	*	+
118		*	*	*	+
119	*		*	*	+
120		*	*	*	+
121	*		*	*	+
122	*		*	*	+
123	*		*	*	+
124	*		*	*	+
125	*		*	*	+
126	*		*	*	+
Кол-во признаков в наборе	50	24	97	100	100

* - признак входит в состав набора.

ПРИЛОЖЕНИЕ 4.
Набор признаков для решения задачи прогнозирования результативности труда преподавателя

3. Возраст 20-25 лет (0 - нет, 1 – да).

4. Возраст 26-35 лет (0 - нет, 1 – да).

5. Возраст 36-60 лет (0 - нет, 1 – да).

6. Пол (1 – мужской, -1 – женский).

7. Семейное положение (0 - неженат/не замужем, 1 - женат/за мужем).

8. Количество детей.

9. Возраст младшего ребенка.

10. Проживает рядом с работой (0 - нет, 1 – да).

11. Образование педагогическое (0 - нет, 1 – да).

12. Работа по специальности (0 - нет, 1 – да).

13. Смежные специальности (0 - нет, 1 – есть).

14. Наличие курсов повышения квалификации (0 - нет, 1 – есть).

15. Перерывы в процессе обучения в Вузе (0 - нет, 1 – есть).

16. Окончание какого Вуза (0 – другой вуз, 1 – институт).

17. Знание иностранных языков (-1 – знания отсутствуют, 0 – знания удовлетворительные, 1 – знания хорошие).

18. Последняя работа педагогическая (0 - нет, 1 – да).

19. Кол-во смененных организаций за последние 5 лет.

20. Наличие повышений по службе (0 - нет, 1 – да).

21. Наличие ученой степени (0 - нет, 1 – да).

22. Обучение в аспирантуре/докторантуре (0 - нет, 1 – да).

23. Ученое звание доцент (0 - нет, 1 – да).

24. Ученое звание доктор (0 - нет, 1 – да).

25. Военнообязанный(ая) (0 - нет, 1 – да).

26. Количество публикаций.

27. Буквы очень маленькие (0 - нет, 1 – да).

28. Буквы маленькие (0 - нет, 1 – да).

29. Буквы средние (0 - нет, 1 – да).

30. Буквы крупные (0 - нет, 1 – да).

31. Наклон букв левый (0 - нет, 1 – да).

32. Наклон букв легкий левый (0 - нет, 1 – да).

33. Наклон букв правый (0 - нет, 1 – да).

34. Наклон букв резкий правый (0 - нет, 1 – да).

35. Прямое написание (0 - нет, 1 – да).

36. Форма букв (-1 – угловатые, 0 – бесформенные, 1 – округлые).

37. Строчки "ползут" (-1 – вниз, 0 – прямые, 1 – вверх).

38. Размашистость почерка (-1 – сильная, 0 – средняя, 1 – легкая).

39. Сила нажима (-1 – сильная, 0 – средняя, 1 – легкая).

40. Стиль написания (-1 – раздельно, 0 – смешанный, 1 – слитно).

41. Почерк индивидуальный (0 - нет, 1 – да).

42. Почерк старательный (0 - нет, 1 – да).

43. Почерк неровный (0 - нет, 1 – да).

44. Почерк небрежный (0 - нет, 1 – да).

45. Длинные петли нижней части букв (0 - нет, 1 – да).

46. Разные по размеру буквы (0 - нет, 1 – да).

47. Большие заглавные буквы (0 - нет, 1 – да).

48. Витиеватость заглавных букв (0 - нет, 1 – да).

49. Угловатые заглавные буквы (0 - нет, 1 – да).

50. Экстравагантные заглавные буквы (0 - нет, 1 – да).

51. Незаконченные петли нижней части букв (0 - нет, 1 – да).

52. Простота написания заглавных букв (0 - нет, 1 – да).

53. Непомерно крупный почерк (0 - нет, 1 – да).

54. Плавный поток ровных букв (0 - нет, 1 – да).

55. Открытые верхние части букв (0 - нет, 1 – да).

56. Лицо овальное (0 - нет, 1 – да).

57. Лицо круглое (0 - нет, 1 – да).

58. Лицо квадратное (0 - нет, 1 – да).

59. Лицо прямоугольное (0 - нет, 1 – да).

60. Лицо треугольное (0 - нет, 1 – да).

61. Брови (-1 – густые, 0 - средние 1 - тонкие).

62. Брови сходятся на переносице (0 - нет, 1 – да).

63. Форма глаз (-1 - круглые, 0 – бесформенные, 1 - миндалевидные).

64. Размер глаз (-1 - большие, 0 - средние, 1 - маленькие).

65. Глаза далеко отстающие друг от друга (0 - нет, 1 – да).

66. Лоб (-1 - низкий, 0 - средний, 1 - высокий).

67. Нос (-1 - острый, 0 – обыкновенный, 1 - курносый).

68. Нос имеет большие "крылья" (0 - нет, 1 – да).

69. Губы (-1 - тонкие, 0 - средние, 1 - пухлые).

70. Подбородок массивный (0 - нет, 1 – да).

71. Подбородок обычный (0 - нет, 1 – да).

72. Подбородок острый (0 - нет, 1 – да).

73. Телосложение (-1 - худощавое, 0 - среднее, 1 - крупное).

74. Вид аккуратный(0 - нет, 1 – да).

75. Стиль торжественный(0 - нет, 1 – да).

ПРИЛОЖЕНИЕ 5.
Анкета “Преподаватель глазами студента”

№	Качество преподавателя	Средний балл
1.	Излагает материал ясно, доступно
2.	Разъясняет сложные и выделяет главные мета
3.	Использует новейшую информацию в данной области
4.	Соблюдает логическую последовательность в изложении
5.	Обеспечивает занятие методическими материалами, пособиями, иллюстрирующими содержание изучаемой темы
6.	Умеет использовать элементы дискуссии и поддержать обратную связь со студентами
7.	Демонстрирует культуру речи
8.	Умеет выбрать оптимальный темп изложения
9.	Умеет снять напряжение и усталость аудитории
10.	Ориентирует на использование изучаемого материала в будущей профессиональной деятельности
11.	Доброжелательность и такт по отношению к студентам
12.	Требовательность к студентам при оценке знаний
13.	Объективность в оценке знаний студентов
14.	Располагает к себе: 14.1. Высокой эрудицией 14.2. Манерой поведения 14.3. Внешним видом
	ИТОГО

ПРИЛОЖЕНИЕ 6.
Результаты экспериментов по реализации алгоритмов дублирования при решении задачи прогнозирования результативности труда преподавателя

Таблица 1

Наборы признаков на базе реализации ПДПР

Порядковый номер признака (описание см. в прил. 4)	Вид набора признаков
Порядковый номер признака (описание см. в прил. 4)	Набор прототипов	Набор дублеров	Набор повышенной надежности
1	2	3	4
3
4		*	*
5
6		*	*
7
8
9
10	*		*
11
12		*	*
13
14		*	*
15
16
17
18	*		*
19		*	*
20		*	*
21
22	*		*
23
24
25		*	*
26
27
28		*	*
29	*		*
30	*		*
31
32
33
34		*	*

Продолжение таблицы 1

1	2	3	4
35	*		*
36
37
38
39
40		*	*
41
42
43		*	*
44	*		*
45
46
47
48		*	*
49	*		*
50	*		*
51
52
53	*		*
54		*	*
55		*	*
56	*		*
57		*	*
58		*	*
59
60
61
62
63
64		*	*
65
66
67		*	*
68
69		*	*
70
71
72
73
74
75
Количество признаков в наборе	11	19	30

* - признак входит в состав набора.

Таблица 2

Наборы признаков на базе реализации КДПР

Порядковый номер признака (описание см. в прил. 4)	Вид набора признаков
Порядковый номер признака (описание см. в прил. 4)	Набор прототипов	Набор дублеров	Набор повышенной надежности
1	2	3	4
3
4		*	*
5		*	*
6
7
8
9
10	*		*
11
12
13		*	*
14
15		*	*
16
17
18	*		*
19
20
21		*	*
22	*		*
23
24
25
26
27
28
29	*		*
30	*		*
31
32
33		*	*
34		*	*
35	*		*
36
37
38
39
40
41		*	*
42

Продолжение таблицы 2

1	2	3	4
43
44
45	*		*
46
47		*	*
48		*	*
49	*		*
50	*		*
51		*	*
52		*	*
53	*		*
54
55		*	*
56	*		*
57
58		*	*
59
60
61
62		*	*
63
64
65
66
67
68
69
70
71
72
73
74
75
Количество признаков в наборе	11	16	27

* - признак входит в состав набора.

Таблица 3

Набор повышенной надежности на базе ПДВР

№ признака

Вид набора

Набор прототипов

Дубль 10-го признака

Дубль 18-го признака

Дубль 22-го признака

Дубль 29-го признака

Дубль 30-го признака

Дубль 35-го признака

Дубль 45-го признака

Дубль 50-го признака

Дубль 51-го признака

Дубль 54-го признака

Дубль 57-го признака

Сколько раз признак является дублером

Набор повышенной надежности

Продолжение таблицы 3

1	2	3		4	5	6	7	8	9	10		11		12	13	14	15
36																0
37																0
38																0
39																0
40																0
41						*						*				2	*
42		*		*	*		*		*							5	*
43												*				1	*
44				*				*								2	*
45	*					*									*	2	*
46								*						*		2	*
47																0
48				*										*		2	*
49						*	*	*	*	*						5	*
50	*	*		*			*		*							4	*
51	*	*			*				*							3	*
52		*							*			*				3	*
53					*			*								2	*
54	*							*				*			*	3	*
55									*			*				2	*
56								*		*				*	*	4	*
57	*									*						1	*
58																0
59					*							*		*		3	*
60																0
61																0
62				*		*									*	3	*
63					*			*				*		*	*	5	*
64																0
65								*	*	*						3	*
66																0
67																0
68		*		*	*				*			*				5	*
69																0
70																0
71							*								*	2	*
72														*	*	2	*
73																0
74									*							1	*
75																0
Кол-во	11	17		15	14	12	15	18	22	10		20		15	13		55

			- признак исключен из набора;								*		- признак входит в набор.

Таблица 4

Набор повышенной надежности на базе КДВР

№ признака

Вид набора

Минимальный набор

Дубль 10-го признака

Дубль 18-го признака

Дубль 22-го признака

Дубль 29-го признака

Дубль 30-го признака

Дубль 35-го признака

Дубль 45-го признака

Дубль 50-го признака

Дубль 51-го признака

Дубль 54-го признака

Дубль 57-го признака

Сколько раз признак является дублером

Набор повышенной надежности

Продолжение таблицы 4

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
36													0
37													0
38													0
39													0
40													0
41		*							*		*		3	*
42		*	*			*			*				4	*
43			*	*					*		*		4	*
44			*			*				*			3	*
45	*												0	*
46			*										1	*
47												*	1	*
48		*		*					*				3	*
49					*				*		*		3	*
50	*												0	*
51	*					*							1	*
52								*	*	*			3	*
53									*				1	*
54	*							*		*			2	*
55								*		*	*	*	4	*
56		*				*						*	3	*
57	*							*		*			2	*
58											*		1	*
59		*					*				*	*	4	*
60												*	1	*
61										*			1	*
62		*							*				2	*
63		*	*					*			*		4	*
64													0
65		*			*						*		3	*
66													0
67			*										1	*
68		*								*			2	*
69													0
70		*					*						2	*
71									*				1	*
72													0
73													0
74							*						1	*
75		*											1	*
Кол-во	11	16	17	8	7	9	6	13	15	14	16	11		61

		- признак переведен в результаты;							*	- признак входит в набор.

Таблица 5

Анализ степени участия признаков в различных видах наборов

Порядковый номер признака	Вид набора					Наличие признака в наборах, (“+”-есть, “-” - нет)
Порядковый номер признака	Минимальный набор	Прямой дубль первого рода	Косвенный дубль первого рода	Прямой дубль второго рода	Косвенный дубль второго рода	Наличие признака в наборах, (“+”-есть, “-” - нет)
1	2	3	4	5	6	7
3				*	*	+
4		*	*	*	*	+
5			*	*	*	+
6		*		*	*	+
7				*	*	+
8					*	+
9						-
10	*			*	*	+
11				*	*	+
12		*		*	*	+
13			*	*	*	+
14		*		*	*	+
15			*	*	*	+
16				*	*	+
17				*	*	+
18	*			*	*	+
19		*		*	*	+
20		*		*	*	+
21			*	*	*	+
22	*			*	*	+
23				*	*	+
24				*	*	+
25		*		*	*	+
26				*		+
27				*	*	+
28		*		*	*	+
29	*			*	*	+
30	*			*	*	+
31				*	*	+
32				*	*	+
33			*	*	*	+
34		*	*	*	*	+
35	*				*	+
36						-
37						-
38						-
39						-
40						-

Продолжение таблицы 5

1	2	3	4	5	6	7
41		*	*	*	*	+
42				*	*	+
43				*	*	+
44		*		*	*	+
45	*			*	*	+
46				*	*	+
47			*		*	+
48			*	*	*	+
49		*		*	*	+
50	*			*	*	+
51	*		*	*	*	+
52			*	*	*	+
53				*	*	+
54	*			*	*	+
55		*	*	*	*	+
56		*		*	*	+
57	*			*	*	+
58		*	*		*	+
59				*	*	+
60					*	+
61					*	+
62			*	*	*	+
63				*	*	+
64						-
65		*		*	*	+
66						-
67					*	+
68		*		*	*	+
69						-
70		*			*	+
71				*	*	+
72				*		+
73						-
74				*	*	+
75					*	+
Кол-во признаков в наборе	11	19	16	55	61	10

* - признак входит в состав набора.

1	2	3	4
37
38
39	*		*
40	*		*
41	*		*
42
43	*		*
44	*		*
45		*	*
46
47		*	*
48		*	*
49	*		*
50		*	*
51	*		*
52	*		*
53
54		*	*
55		*	*
56
57	*		*
58
59
60	*		*
61	*		*
62
63
64
65
66	*		*
67
68
69	*		*
70	*		*
71	*		*
72
73	*		*
74
75	*		*
76	*		*
77	*		*
78		*	*
79
80
81
82
83	*		*

1	2	3	4	5	6
41	*		*	*	+
42					-
43	*		*	*	+
44	*		*	*	+
45		*	*	*	+
46			*	*	+
47		*	*	*	+
48		*	*	*	+
49	*		*	*	+
50		*	*	*	+
51	*		*	*	+
52	*		*	*	+
53					-
54		*	*	*	+
55		*	*	*	+
56			*	*	+
57	*		*	*	+
58			*	*	+
59			*	*	+
60	*		*	*	+
61	*		*	*	+
62					-
63					-
64					-
65					-
66	*		*	*	+
67					-
68					-
69	*		*	*	+
70	*		*	*	+
71	*		*	*	+
72					-
73	*		*	*	+
74			*	*	+
75	*		*	*	+
76	*		*	*	+
77	*		*	*	+
78		*	*	*	+
79			*	*	+
80			*	*	+
81			*	*	+
82					-
83	*		*	*	+
84				*	+

1	2	3	4
37
38
39	*		*
40	*		*
41	*		*
42
43	*		*
44	*		*
45		*	*
46
47		*	*
48		*	*
49	*		*
50		*	*
51	*		*
52	*		*
53
54		*	*
55		*	*
56
57	*		*
58
59
60	*		*
61	*		*
62
63
64
65
66	*		*
67
68
69	*		*
70	*		*
71	*		*
72
73	*		*
74
75	*		*
76	*		*
77	*		*
78		*	*
79
80
81
82
83	*		*

1	2	3	4	5	6
41	*		*	*	+
42					-
43	*		*	*	+
44	*		*	*	+
45		*	*	*	+
46			*	*	+
47		*	*	*	+
48		*	*	*	+
49	*		*	*	+
50		*	*	*	+
51	*		*	*	+
52	*		*	*	+
53					-
54		*	*	*	+
55		*	*	*	+
56			*	*	+
57	*		*	*	+
58			*	*	+
59			*	*	+
60	*		*	*	+
61	*		*	*	+
62					-
63					-
64					-
65					-
66	*		*	*	+
67					-
68					-
69	*		*	*	+
70	*		*	*	+
71	*		*	*	+
72					-
73	*		*	*	+
74			*	*	+
75	*		*	*	+
76	*		*	*	+
77	*		*	*	+
78		*	*	*	+
79			*	*	+
80			*	*	+
81			*	*	+
82					-
83	*		*	*	+
84				*	+

1	2	3	4
37
38
39	*		*
40	*		*
41	*		*
42
43	*		*
44	*		*
45		*	*
46
47		*	*
48		*	*
49	*		*
50		*	*
51	*		*
52	*		*
53
54		*	*
55		*	*
56
57	*		*
58
59
60	*		*
61	*		*
62
63
64
65
66	*		*
67
68
69	*		*
70	*		*
71	*		*
72
73	*		*
74
75	*		*
76	*		*
77	*		*
78		*	*
79
80
81
82
83	*		*

1	2	3	4	5	6
41	*		*	*	+
42					-
43	*		*	*	+
44	*		*	*	+
45		*	*	*	+
46			*	*	+
47		*	*	*	+
48		*	*	*	+
49	*		*	*	+
50		*	*	*	+
51	*		*	*	+
52	*		*	*	+
53					-
54		*	*	*	+
55		*	*	*	+
56			*	*	+
57	*		*	*	+
58			*	*	+
59			*	*	+
60	*		*	*	+
61	*		*	*	+
62					-
63					-
64					-
65					-
66	*		*	*	+
67					-
68					-
69	*		*	*	+
70	*		*	*	+
71	*		*	*	+
72					-
73	*		*	*	+
74			*	*	+
75	*		*	*	+
76	*		*	*	+
77	*		*	*	+
78		*	*	*	+
79			*	*	+
80			*	*	+
81			*	*	+
82					-
83	*		*	*	+
84				*	+